
kogn_motpk_lection_4
.pdf11
Процедура перемножения многочленов по тактам |
Таблица 3.1. |
|||
|
|
|
|
|
|
№ такта |
Вход |
Выход |
|
|
|
|
|
|
|
1 |
аn |
anbk |
|
|
2 |
аn-1 |
an-1bk+anbk-1 |
|
|
3 |
аn-2 |
an-2bk+an-1bk-1+anbk-2 |
|
|
4 |
аn-3 |
an-3bk+an-2bk-1+an-1bk-2+anbk-3 |
|
|
…… |
……. |
……. |
|
|
|
|
|
|
|
n+k-1 |
0 |
a0b1+a1b0 |
|
|
|
|
|
|
|
n+k |
0 |
a0b0 |
|
Рассмотрим некоторые характерные особенности построения этих схем для многочленов с двоичными коэффициентами, а именно с коэффициентами 0 и 1.
Умножение на величину bi производим по правилу:
для bi=0: aj bi= aj 0=0 и для bi = 1: aj bi= aj 1=aj.
Таким образом, умножение на 0 соответствует разорванной цепи, а умножение на
1 – короткому замыканию.
12
Пример умножения. Пусть даны два многочлена с коэффициентами из двоичного
поля |
|
f1(x) = 1 + х3 + х4 + х6 + x8, |
f2(x) = х + х2 + х3 |
Их произведение после приведения коэффициентов по модулю 2 будет равно: f(x) = f1(x)∙f2(х) = х + х2 + х3 + х4 +х8+ х10+ х 11
Многочлену f1(x) соответствует комбинация (100110101), а многочлену f2(х) – (0111). Начало комбинации соответствует младшему разряду, т. е. нулевой степени х.
Умножение f1(x)∙f2(x) в двоичном представлении:
f1(x) (1 0 0 1 1 0 1 0 1) ×0 0 0 0 0 0 0 0 0 0
×1(x) |
1 0 0 1 1 0 1 0 1 |
× f2(x) |
×1(x2) |
1 0 0 1 1 0 1 0 1 |
|
×1(x3) |
1 0 0 1 1 0 1 0 1 |
|
(0 1 1 1 1 0 0 0 1 0 1 1);
13
Пусть, например, f2(x) = 1 + x + х3 + х5, т. е. b0 = 1, b1 = 1, b2=0, b3= 1, b4 = 0, b5 = 1.
Выход
|
b0=1 |
|
|
b1=1 |
|
b2=0 |
|
|
|
b3=1 |
|
b4=0 |
|
|
|
b5=1 |
||||
Вход |
x0 |
|
|
x1 |
|
x2 |
|
|
|
x3 |
|
x4 |
|
|
|
x5 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выход |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
|
|
x1 |
|
|
|
|
|
x3 |
|
|
5 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||
Вход
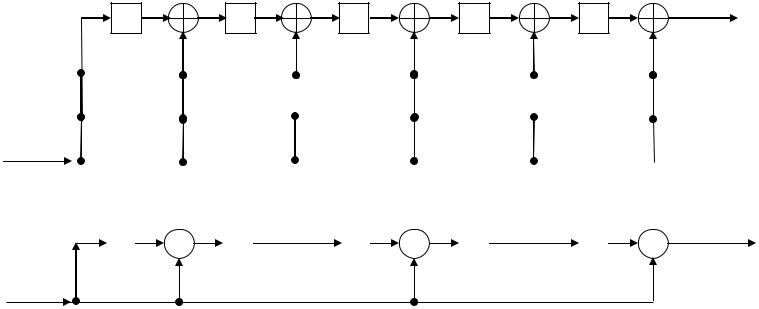
Рис. 3.4. Пример реализации умножения на основе регистра со встроенными сумматорами.
Аналогично строится регистр умножения с вынесенными сумматорами.

Деление многочленов |
14 |
Операция деления многочленов осуществляется по обычным правилам деления с приведением коэффициентов по modр. Например, деление двоичных многочленов (р = 2) осуществляется следующим образом:
x8 +x6 + x4 + x3 +1 |
|
|
|
2 |
+ x |
|
|
|
|
|
||||
|
|
3 |
|
|
|
|
||||||||
x8 +x7 + x6 |
|
|
|
x |
+x |
|
|
|
|
|||||
|
|
|
x5 + x4 + x3 +1 |
Деление f1(x):f2(x) в двоичном виде. |
||||||||||
x7 + x4 + x3 +1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
При делении комбинации f1(x) и f2(x) |
||||||
x7 + x6 + x5 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
записывают в двоичной форме со старшего |
|||
|
x6 +x5 + x4 + x3 |
+1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
разряда и делят следующим образом: |
||||||||
|
x6 +x5 + x4 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 +1 |
|
|
|
|
f (x) |
|
f (x) |
||
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
||
|
|
|
|
|
x3 +x2 + x |
101011001 |
|
1110 |
||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
1110 |
|
111001 x5+ x4+ x3+1 (частное) |
|
|
|
|
|
|
x2 + x +1 (остаток) |
|
|
||||||
|
|
|
|
|
|
1001 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
1110 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
1111 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1110 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0010 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1110 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1110 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1001 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1110 |
|
|
|
111 x2+x+1 (остаток)

15
В общем виде операция деления может быть записана так:
a xn |
a |
1 |
xn 1 |
... a x a |
|||||||||||||||
|
|
n |
|
n |
|
|
|
|
|
1 |
0 |
|
|||||||
|
an |
b xn |
an |
b |
|
xn 1 |
... |
an |
b xn k |
||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
k |
|
|
|
|
|
k 1 |
|
|
|
0 |
|||||
|
bk |
|
|
|
bk |
|
|
|
|
|
|
bk |
|||||||
(a |
|
an |
b |
)xn 1 ... (a |
|
|
an |
b )xn k |
|||||||||||
|
n k |
|
|||||||||||||||||
n 1 |
|
|
bk |
|
k 1 |
|
|
|
|
|
|
|
0 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bk |
||||
bkxk + bk-1xk-1 + … +b1x + b0
an xn k ....
bk
... a1x a0
При этом коэффициенты |
(an 1 |
|
an |
bk 1 ),...(an k |
|
an |
b0 ) |
приводятся по модулю р. |
|
|
|||||||
|
|
|
bk |
|
bk |
Выход |
||
|
|
|
|
|
|
|
|
|
–b0 |
–b1 |
–b2 |
–b |
k-1 |
1 |
|
|
|
|
bk |
|
|
|
|
|
|
Вход f1(x)
Рис. 3.5. Схема деления на многочлен f2 (x) b0 b1x b2 x2 ... bk xk

16
Пример. Пусть f (x) = 1 + х2 |
+ х4 + х5, т. е. b |
0 |
= 1, b = 0, b = 1, b |
3 |
= 0, b = 1, b |
5 |
= 1. |
|||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
1 |
2 |
|
4 |
|
|||||||||||||
На рис. 3.6 представлена схема деления на заданный |
многочлен. |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выход |
|
|
1 |
|
|
|
|
|
|
x2 |
|
|
|
|
x4 |
|
|
x5 |
|
|
|||||||||
Вход |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.6
Выход
–b0 |
–b1 |
–b2 |
–bk-1 |
b 1 |
|
|
|
|
k |
c0 |
c1 |
c2 |
ck-1 |
ck |
Вход
Рис. 3.7. Схема, реализующая одновременное умножение на многочлен h(x)= c0+ c1x + .. + ckxk и деление на многочлен g(x)=b0+blx+b2x2+ ... +bkхk

Реализация операций одновременного умножения и деления |
17 |
многочленов в поле двоичных чисел. |
|
1 |
x3 |
x4 |
x5 |
x6 |
Выход
1 |
x |
x5 |
Вход
а)
Выход
1 |
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
x4 |
|
|
|
x5 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x5 |
x9 |
Вход
б)
Рис. 3.8. Примеры схем, реализующих одновременное умножение на многочлен h(x) и деление на многочлен g(x) для:
а) h(x)= 1+ x + x5 б) h(x)= 1+ x5 + x9
иg(x)=1+x3+x4+ x5+ x6;
иg(x)=1+x3+x4+ x5
Сравнение полиномов по модулю |
18 |
n
Определение 1. Полином A(x) ai xi a0 a1x a2 x2 ... an xn
i 0
называется полиномом над полем GF(p), если его коэффициенты ai принадлежат полю GF(p).
Определение 2. Сравнение полиномов по модулю F(x). Полином А(х) сравним с полиномом В(х) по модулю F(x), т.е. А(х) В(х) modF(x), если разность А(х) – В(х) делится на F(x) без остатка.
Определение 3. Сравнение полиномов по двойному модулю F(x) и p. Если при сравнении полиномов А(х) и В(х) по модулю F(x) все коэффициенты, кроме того, приводятся по модулю p, то тогда говорят, что полином А(х) сравним с полиномом В(х) по двойному модулю (F(x), p),что записывается как А(х) В(х) modd(F(x),p) .
Определение 4. Если дан полином F(x) степени n над полем GF(p), то любому полиному А(х) степени m (m≥n) будет соответствовать остаток R(x) от деления А(х) на F(x), т.е. А(х) R(х) modd(F(x),p). При этом R(x) – это вычет по двойному модулю modd(F(x),p), который представляет собой полином степени не выше (n-1)
n 1
R(x) ri xi r0 r1x r2 x2 ... rn 1xn 1
i 0
где ri GF(p).

Эварист Галуа. Нестандартность. Путь гения.
Эварист Галуа (26 октября 1811 – 31 мая 1832) – выдающийся французский математик, основатель современной высшей алгебры
Галуа успел в свои 21 год состояться как математик, да такой что не знала Франция со времен Декарта. Был убит на глупой дуэли. Его заметки опубликовали через 15 лет. Стали нужны математике еще через 50 лет. Маленький ручеѐк идеи стал огромной рекой. Обычная судьба гения.
За 20 лет жизни Галуа успел сделать открытия, ставящие его на уровень крупнейших математиков XIX века. Решая задачи по теории алгебраических уравнений, он заложил основы современной алгебры, вышел на такие фундаментальные понятия, как группа (Галуа первым использовал этот термин, активно изучая симметрические группы) и поле (конечные поля носят название полей Галуа).
Эварист Галуа предсмертное стихотворение в 21 год
Ижизнь пройдет, как тихие дожди, Загадка, не разгаданная нами… Осталось на костѐр судьбы взойти
Икануть в пожирающее пламя…
Сгореть нестрашно, страшно дымом стать… Развеяться, растаять, раствориться, Исчезнуть, до конца сумев понять, Что в этой жизни есть к чему стремиться… Мир нем и глух, застлал глаза туман.
Как страшно все, и все-таки я верю, Что вечность есть, что это не обман, Что найдены распахнутые двери.
Ичто разгадки тайн всегда просты.
Истали вдруг доступны пониманью Возможность нереальная мечты
Ихрупкость моего существованья…
