
- •Содержание
- •1. Зубчатый механизм
- •1.1. Определение общего передаточного отношения и подбор чисел зубьев колес
- •1.2. Кинематический расчет редуктора
- •1.2.1. Частоты вращения звеньев
- •1.3. Геометрический синтез зубчатой пары
- •1.3.1. Предварительный выбор коэффициентов смещения колес
- •1.3.2. Округление межосевого расстояния и уточнение коэффициентов смещения
- •1.3.3. Основные геометрические размеры колес передачи
- •1.3.4. Проверка качества зацепления по геометрическим показателям
- •1.3.5. Расчет измерительных размеров
- •1.3.6. Картина зацепления
- •2. Анализ и синтез рычажного механизма
- •2.1 Исходные данные
- •2.2. Кинематический анализ рычажного механизма
- •2.2.1. Структурный анализ механизма
- •2.2.2. Построение заданного положения механизма
- •2.2.3. Определение линейных и угловых скоростей.
- •Начальный механизм [6,1]
- •Группа (2,3)
- •Группа (4,5)
- •2.2.4. Определение линейных и угловых ускорений. Начальный механизм [6.1]
- •Группа (2,3)
- •Группа (4.5)
- •2.3. Кинетостатический анализ рычажного механизма
- •2.3.1. Определение внешних нагрузок
- •2.3.2. Определение реакций в кинематических парах и уравновешивающего момента методом планов сил
- •Группа (4,5)
- •Группа (2,3)
- •Группа [6,1]
- •2.3.3. Определение уравновешивающего момента методом н.Е. Жуковского
- •2.3.4. Сравнение значений уравновешивающего момента, полученных различными методами
- •2.3.5. Оценка потерь мощности на преодоление сил трения в кинематических парах
- •3. Кулачковый механизм
- •3.1. Кинематические диаграммы
- •3.2. Определение наивыгоднейших размеров кулачка
- •3.3. Построение профиля кулачка
2. Анализ и синтез рычажного механизма
2.1 Исходные данные

tц=0.45 c,
Тпс =800 Н·м,
Параметры звеньев механизма:
Длина кривошипа ОА= 0.5 м ;
Остальные размеры заданы соотношениями:
ОА= ОС / (3.75…3.80) ;
BS2= (0.65…0.70)AB ;
СS3= (0.35…0.40)BC ;
ES5= (0.40…0.45) (DE)max
Соотношения для масс и моментов инерции звеньев:
m4 = 7 кг ; m2 = 12·m4 ; m3 = 5·m4 ; m5 = 9·m4 ;
Js4 = 0.3 кг·м2 ; Js2 = 10·Js4 ; Js3 = 6·Js4 ; Js5 = 8·Js4 ;
Примем:
OA = 0.5 м ; AB = 1.12 м ; BC = 0.7 м ; AD = 0.6 м ; DE = 0.35 м ;
2.2. Кинематический анализ рычажного механизма
2.2.1. Структурный анализ механизма
Степень подвижности механизма определим по формуле Чебышева:
 ,
(2.1)
,
(2.1)
где
 – число
подвижных звеньев механизма;
– число
подвижных звеньев механизма;
 –
число
кинематических пар 4 класса;
–
число
кинематических пар 4 класса;
 –
число
кинематических пар 5 класса;
–
число
кинематических пар 5 класса;
получим:
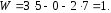
За начальное звено принимаем кривошип ОА, так как для него задан закон движения. Формула строения механизма в этом случае:
[6,1]
(2,3)
(2.2)

(4,5),
где
[6,1] – начальный механизм I класса;
(2,3) – структурная группа II класса 1 вида;
(4,5) – структурная группа II класса 3 вида.
Таким образом, данный механизм является механизмом II класса.
2.2.2. Построение заданного положения механизма
Примем масштаб изображения механизма на чертеже:
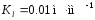 .
.
Отрезки на чертеже будем обозначать со знаком “ ~ “.
Длины звеньев на чертеже:
 =50
мм;
=50
мм;
 =112
мм;
=112
мм;
 =70
мм;
=70
мм;
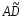 =60
мм;
=60
мм;
 =35
мм;
=35
мм;
2.2.3. Определение линейных и угловых скоростей.
Кинематический анализ механизма выполняем для заданного положения механизма в порядке присоединения структурных групп согласно формуле (2.2).
Начальный механизм [6,1]
Скорость точки А :
 .
(2.3)
.
(2.3)
Вектор
 направлен из полюса плана скоростей
Pv
перпендикулярно кривошипу ОА
по направлению угловой скорости ω1;
конец этого вектора на плане скоростей
– точка а.
направлен из полюса плана скоростей
Pv
перпендикулярно кривошипу ОА
по направлению угловой скорости ω1;
конец этого вектора на плане скоростей
– точка а.
Определим масштабный коэффициент плана скоростей :
 .
(2.4)
.
(2.4)
Группа (2,3)
Скорость точки В :
 (2.5)
(2.5)
В
первом уравнении вектор
 направлен перпендикулярно звену АВ.
Во втором уравнении точка С
неподвижна
(
направлен перпендикулярно звену АВ.
Во втором уравнении точка С
неподвижна
( )
и конец вектора
)
и конец вектора
 (точка с)
совпадает с полюсом плана скоростей
Pv.
Вектор
(точка с)
совпадает с полюсом плана скоростей
Pv.
Вектор
 направлен перпендикулярно звену BC.
направлен перпендикулярно звену BC.
В
результате построения находим точку
b
– конец вектора
 :
:
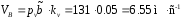 ;
; .
.
В
этих формулах
 и
и
 – длины (в миллиметрах) отрезков плана
скоростей.
– длины (в миллиметрах) отрезков плана
скоростей.
Угловая скорость звена механизма определяется по параметрам относительной скорости любых двух точек, принадлежащих этому звену.
Угловая скорость 2-го звена :
 .
.
Угловая скорость 3-го звена :
 .
.
