2. Примеры решения задач

Задача №1.

Определить длину фланговых швов, обеспечивающих прочность соединения равнобокого уголка и косынки (рис. 1.4,а), если размеры поперечного сечения уголка 70х70х6, материал сталь Ст3, сварка ручная электродом Э42, нагрузка изменяется по отнулевому циклу (r = 0).

Решение

1. По таблице справочника [2] принимаем с =70 мм, t =6 мм, площадь поперечного сечения уголка А = 813 мм² , =19,3 мм.

Допускаемое напряжение (табл. 1.1) при статическом растяжении основного материала равно =160 МПа. Допускаемое напряжение для материала уголка в зоне шва при переменной нагрузке равно:

Коэффициент снижения допускаемого напряжения материала детали (уголка) определим по формуле (1.24), в которой r =0, (для углеродистых сталей), (по табл. 1.2)

Тогда

.

2. Исходя из условия прочности уголка на растяжение, определяем допускаемое значение растягивающей силы

.

По этой силе ведем расчет сварного шва, то есть обеспечим равнопрочность уголка на растяжение и шва на срез.

3. По табл. 1.1, 1.2 и формуле (1.24) определяем допускаемое напряжение шва на срез при переменной нагрузке

.

4. Из условия прочности швов (1.21) определяем их суммарную длину (), принимая катет шва k = t =6 мм:

.

5. Соблюдая условие равнопрочности, швы выполняют с различной длиной так, что

,

Учитывая возможность технологических дефектов сварки, окончательно принимаем

Задача № 2

Рассчитать сварное соединение двутавровой балки с колонной (рис.2.1).

Дано: F = 8кН, L = 1.5м.

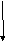
Рис. 2.1

Решение.

1.Определяем сечение двутавровой балки по условию её прочности:

σ = ≤[σ] ,

где

М_и – изгибающий момент, действующий на балку от силы F в месте

её заделки;

W – осевой момент сопротивления площади поперечного сечения

балки.

М_и = FL = 8000·1500 = 12х10⁶ Н·мм

Примем, что балка изготовлена из стали Ст.3 (σ_т=220 МПа).

Тогда

[σ] = σ_т/s,

где s – коэффициент запаса прочности, s = 1,4 [1, с.75].

[σ] = 220/1,4 = 157 МПа.

Учитывая только основную нагрузку, действующую на балку от момента М_и, получаем:

W = =76,43·10³ мм³.

Выбираем двутавр (с учётом действия силы F) № 16.

Для него имеем:

h=160 мм, в=81 мм, d=5 мм, t=7.8 мм, W_x=109х10³ мм³, J_х=873·10⁴ мм⁴ (см. рис. 2.2) [2, с.118].

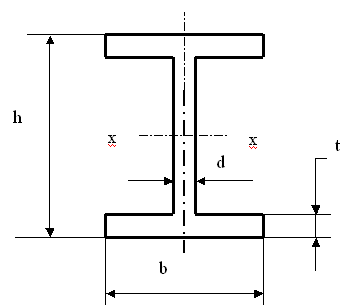
Рис. 2.2

Проверим прочность балки при суммарной (полной) нагрузке:

; .

А – площадь поперечного сечения балки.

А = 2bt + (h – 2t)d = 2·81·7,8 + (160 – 2·7,8)·5 = 1985,6 мм².

и

<.

Прочность балки обеспечена!

2. Задаёмся размерами сварного шва и проверяем его на прочность

Длина сварного углового шва определяется размерами периметра двутавровой балки, а катет шва примем – к = d = 5 мм.

Условие прочности сварного шва:

τ =

здесь

- напряжения в шве от силы F и направлено оно по вертикальной оси;

- напряжение от момента М. Оно изменяется по линейному закону (как напряжения изгиба) и направлено по горизонтальной оси;

[τ^'] – допускаемое напряжение для сварного шва (табл. 1.1).

[τ^'] = 0.6[σ_р] = 0.6·157 = 94 МПа.

= , а =

где

А₁ и W₁ – площадь поперечного сечения сварного шва и её осевой момент сопротивления.

А₁ = 4·0.7кt + 2·0.7кb + 2·0.7к(h – 2t) + 2·0.7к(b-d) =

= 4·0,7·5·7,8 + 2·0,7·5·81 + 2·0,7·5 (160 -2·7,8) + 2·0,7·5(81 – 5) = 2219 мм².

W₁ = = ,

J₁ – момент инерции площади поперечного сечения сварного шва относительно оси х-х (рис.2.2).

Контур сварного шва изображён на рис. 2.3 и катет шва по всему контуру равен к = 5 мм.

J₁ = J_н – J_б,

где

J_н - момент инерции площади поперечного сечения по наружному контуру шва,

J_б - момент инерции площади поперечного сечения балки (по внутреннему контуру шва) и равен J_б = J_х = 873·10⁴ мм⁴.

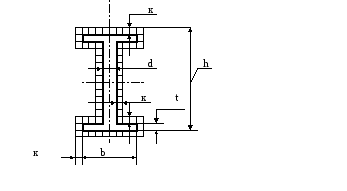
Рис. 2.3.

J_н = - (b+2·0,7К) +

+= (81+2·0,7·5) -

-(81+2·0,7·5) + = 16.65·10⁶ мм⁴.

J₁ = 16,65·10⁶ – 8,73·10⁶ = 7,92·10⁶ мм⁴

W₁ = .= 99·10³ мм³.

3,6 МПа; 121 МПа.

= 121 МПа> = 94 МПа.

Таким образом, прочность сварного шва не обеспечена!

Возьмём следующий размер двутавра №18.

Для него имеем:

h = 180 мм, b = 90 мм, d = 5.1 мм, t = 8.1 мм, J_x = 1290х10⁴ мм⁴,

W_x = 143x10³ мм³. [2, с.118].

Параметры сварного шва определим по принципу, использованному ранее:

длина шва – определяется обходом по контуру двутавра, а катет шва К = 5 мм.

А₁ = 40,7·5·8,1 + 2·0,7·5·90 + 2·0,7·5(180 – 2·8,1) + 2·0,7·5(180-5,1) =3114 м².

J_Н = (90+2·0,7·5) - (90+2·0,7·5) +

+ = 23.95·10⁶ мм⁴,

J₁ = 23.95·10⁶ – 12.9·10⁶ =11,05·10⁶ мм⁴,

W₁ = = 122.8·10³ мм³.

= 2.57 МПа; = 95 МПа;

Таким образом МПа = 94 МПа.

Расхождение составляет 3.9%, что допустимо (менее 5%).

Прочность шва обеспечена.

Задача № 3.

Рассчитать сварное соединение двух уголков с плитой (рис. 2.4).

Д

ано: сила, действующая на уголок, F = 80 кН, угол α = 20⁰.

Решение

1. Определяем сечение уголков по условию их прочности.

1.1. Определяем силы, действующие на уголки 1 и 2 (Рис. 2.4).

Для этого строим силовой треугольник. (Рис. 2.5).

Имеем: С = 50⁰, D = 60⁰, В = 180⁰ – C – D = 180⁰ – 50⁰ – 60⁰ = 70⁰.

Для определения сил, действующих на уголки, воспользуемся теоремой синусов:

, тогда

F₁ = Н,

2

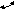
Рис. 2.4.

F₂

F

30⁰

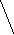
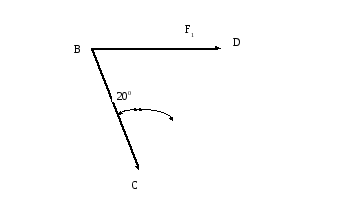
Рис.. 2.5.

F₂ = Н.

Поскольку сила F₂ = 75175 Н, действующая на уголок 2, больше силы

F₁ = 70764 Н, действующей на уголок 1, то расчёт на прочность уголков будем вести по силе F₂.

2. Расчёт на прочность уголков.

Условие прочности:

,

где А – площадь поперечного сечения уголка,

- допускаемое напряжение сжатия материала уголка.

- предел текучести материала уголка.

s – коэффициент запаса прочности.

Примем, что уголки изготовлены из стали Ст.3 (= 220 МПа), s = 1.4 [1].

Тогда == 157 МПа.

А239.4 мм².

Примем уголок № 4.5 (равнобокий). Для него имеем: b=45мм, d=3мм, z₀=12,1мм, А=265мм² (Рис. 2.6). [2, с.112]

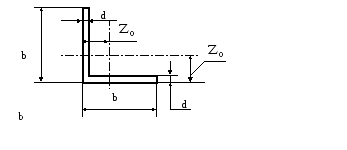
Рис. 2.6.

2. Расчёт прочности сварных швов.

2.1. Расчёт прочности швов для уголка 1 (Рис. 2.4).

Сила F_Г (Рис. 2.7), действующая на один уголок, равна:

F_Г = 35382 Н.

Условие прочности сварного шва:

.

Примем катет шва к = 3мм, (табл. 1.1),

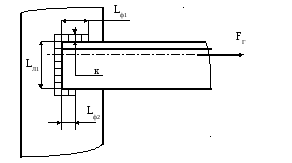
Рис. 2.7.

МПа.

Суммарная длина шва равна:

(

(

Соотношение между длинами швов ( и расстояниями полочек уголка от точки О (Рис. 2.6) таково:

[1, с. 69, форм. 3.5],

( в ).

Решая совместно уравнения а и в получаем:

2.2. Расчёт прочности сварных швов для уголков 2 (Рис. 2.4).

Сила, действующая на один уголок, равна:

F_В = F₂/2 = 75175/2 = 37588 Н.

Условие прочности сварного шва:

.

Суммарная длина швов равна:

Так же как и для сварного шва уголка 1 (Рис. 2.4).примем

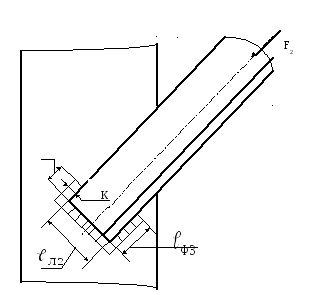
Рис. 2.8.

. (б)

(с)

Решая совместно уравнения б и с получаем:

Кроме того, для всех сварных фланговых швов выполняется условие:

К = 3 мм < 50 = 50

Задача № 4

Рассчитать сварное соединение двух частей клеммового рычага (см. рис.2.9), если сила F = 2000 Н, толщина пластины S = 10 мм, расстояние L= 600 мм.

Решение

1.Определяем ширину приваренного рычага из условия его прочности по нормальным напряжениям при изгибе:

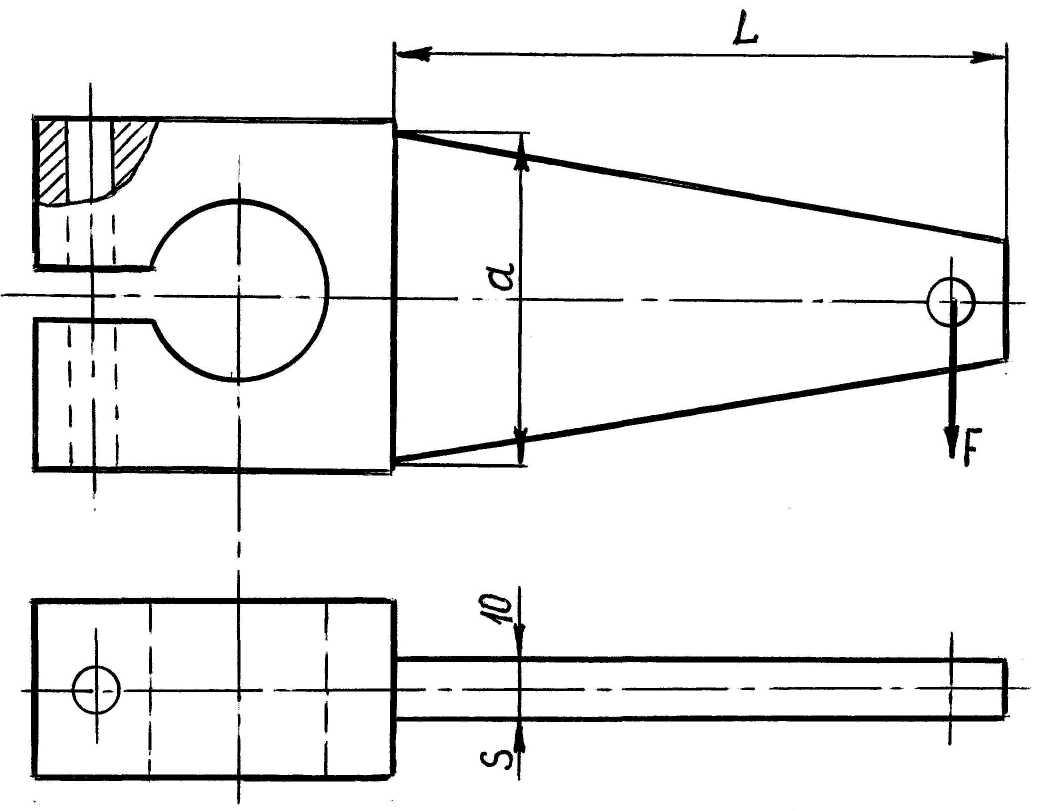
Рис. 2.9

где М_И – изгибающий момент, действующий в сечении рычага в месте сварки:

М_И = FL = 2000600 = 1210⁵ МПа;

W_ОС – осевой момент сопротивления площади поперечного сечения рычага: . Толщина пластины S = 10 мм.

Допускаемые напряжения для стали. Принимаем, что рычаг изготовлен из стали Ст. 3 (_Т = 220 МПа).

Тогда

,

где [S] – коэффициент запаса прочности ([S] = 1,4).

Осевой момент сопротивления при условии _max =[s].

мм³ .

Определяем ширину пластины

мм.

Принимаем бо^/льшее значение а = 70мм.

Проверяем условие прочности рычага при изгибе

,

где .

2. Расчет сварного соединения.

Рассмотрим два варианта выполнения сварного соединения:

1. тавровое соединение с разделкой кромок – шов стыковой (рис. 2.10,а);

2. тавровое соединение без разделки кромок – шов угловой (рис. 2.10,б).

а. б.

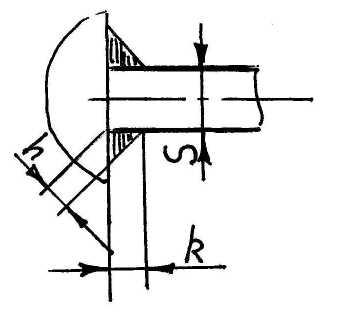
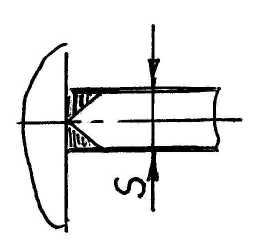
Рис. 2.10

1. Расчёт таврового соединения с разделкой кромок – шов стыковой.

Условие прочности шва s_max  [_Р].

Действующие напряжения в шве

,

где W_ОС – осевой момент сопротивления площади поперечного сечения шва, равен осевому моменту сопротивления площади поперечного сечения рычага. Примем, что сварка выполнена электродом Э – 42 вручную, тогда допускаемые напряжения для шва (табл. 1.1)

[_Р] = 0,9[s_Р], где [s_Р] = 157 Мпа, тогда [_Р] = 0,9 157 = 141,3 Мпа.

Таким образом, условие прочности для стыкового шва не выполняется. Здесь не учитываются напряжения среза от силы F, действующей в плоскости шва

.

Увеличиваем ширину пластины “а”, которую теперь определим из условия прочности шва s_max  [_Р].

Осевой момент сопротивления площади поперечного сечения шва

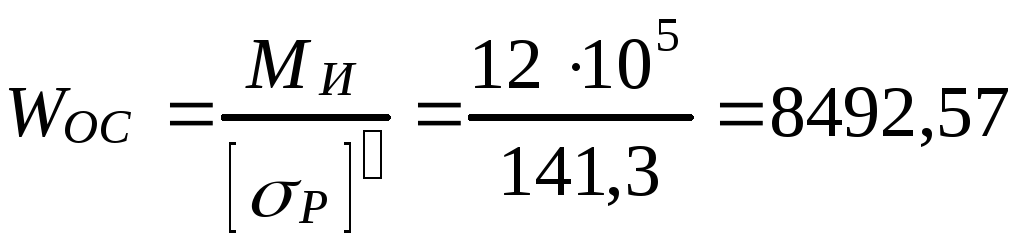мм³.

Ширина пластины

.

Принимаем ширину пластины “а” больше, т.е. а = 75 мм.

Окончательно проверяем стыковой шов на прочность

,

где осевой момент сопротивления площади поперечного сечения шва

.

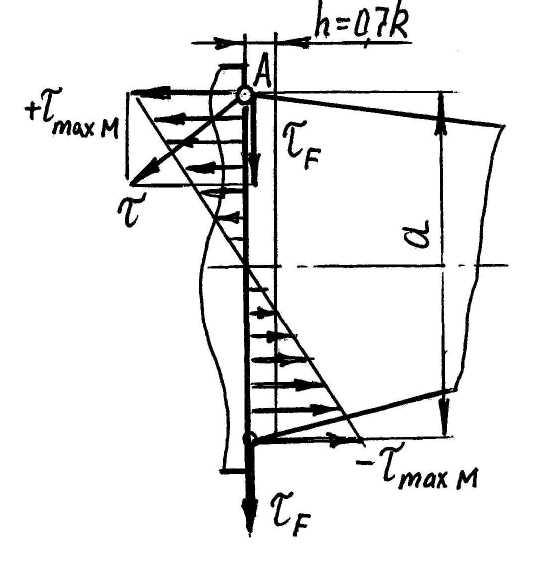
2. Расчёт таврового соединения без разделки кромок – шов угловой (рис. 2.10,б). Расчёт ведём по касательным напряжениям среза. Пластину привариваем по периметру (см. рис. 2.12). Наибольшие напряжения _max действуют в точке “а” (см. рис. 2.11), где взаимодействуют максимальные напряжения _{max М} от изгибающего момента и касательные напряжения среза от силы F в плоскости шва. Результирующие напряжения в точке “а”

t_max = t_{max М} + t_F,

или .

Здесь [] допускаемые напряжения для углового шва. Если, как и ранее, сварка выполнена электродом Э – 42 вручную, то по табл. 1.1

[] = 0,6 [s_Р] = 0,6157 = 94,2 Мпа.

Напряжения от изгибающего момента

.

Рис. 2.11

Осевой момент сопротивления шва двух швов (см. рис. 1.12) мм³.

В этой формуле h  0,7k – толщина углового шва в месте возможного разрушения, k – катет шва. Обычно принимается для углового шва выполненного ручной сваркой k = S = 10 мм.

Рис. 2.12

Пренебрегая напряжениями среза tF определим длину шва из его условия прочности tmax М = []. . Откуда Ширина пластины “a” равная длине шва . Окончательно принимаем а = 75 мм. Проверочный расчет с учетом напряжений среза

где площадь среза для шва (см. рис. 2.12)

А_СРЕЗА = 2(а+20,7k) +2S0,7k = 2(75 +2×0,7×10) + 10×0,7×10 = 248 мм².

Результирующие касательные напряжения

Здесь

Прочность сварного шва обеспечена.

Ответ. Длина сварного шва: стыкового – а = 75 мм: углового – а = 75 мм.

Задача №5.

Определить размеры h и  листов 1 и 2 (рис. 2.13), прикрепленных к швеллерам колонны и рассчитать сварные швы по следующим данным: сила F = 8 кН, плечо силы L = 800 мм.

Решение

1.Определяем размеры h и d из условия прочности листов при изгибе

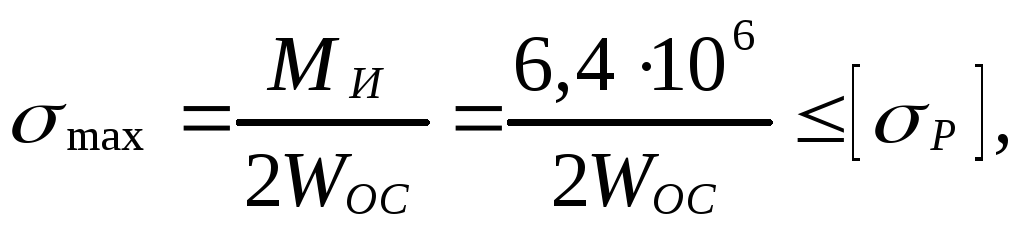
где М_И – изгибающий момент, действующий в сечении двух листов по оси швеллера

М_И = FL = 8000800,0 = 6,4 10⁶ Нмм.

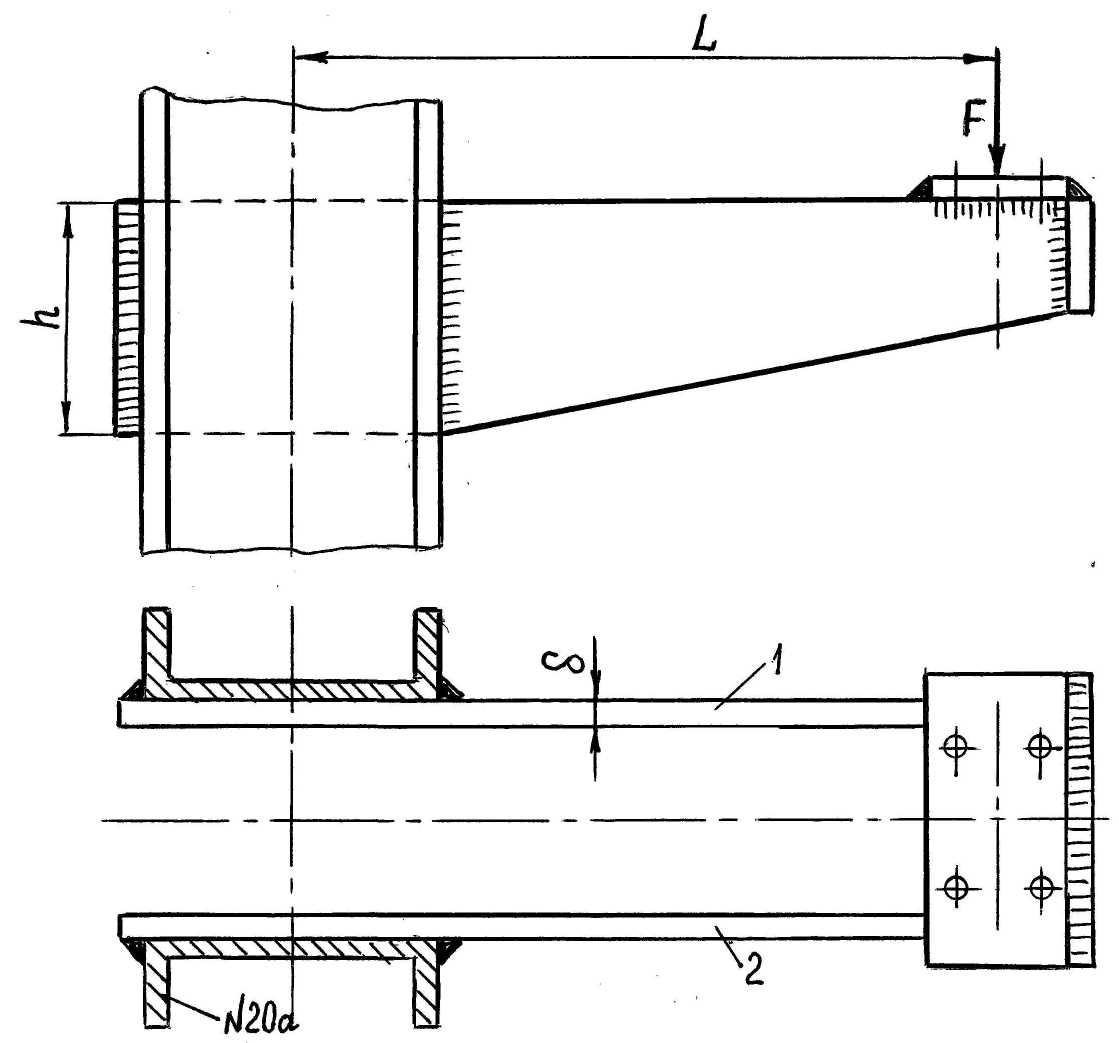
Рис. 2.13

Осевой момент сопротивления площади поперечного сечения одного листа

мм³.

Здесь допускаемые напряжения [s_Р] для стали.

,

Принимаем, что рычаг изготовлен из стали Ст. 3 (s_Т = 240 МПа).

[S] – коэффициент запаса прочности ([S] = 1,4).

Осевой момент сопротивления сечения одного листа

.

Примем, что толщина листа d = 10 мм.

Откуда ширина листа

.

Окончательно примем h = 110 мм.

2. Расчет сварных швов. Так как сварное соединение выполнено угловыми швами, то расчёт ведём по касательным напряжениям (см. раздел 1.2). Находим центр тяжести сечения сварных швов (см. рис. 2.14).

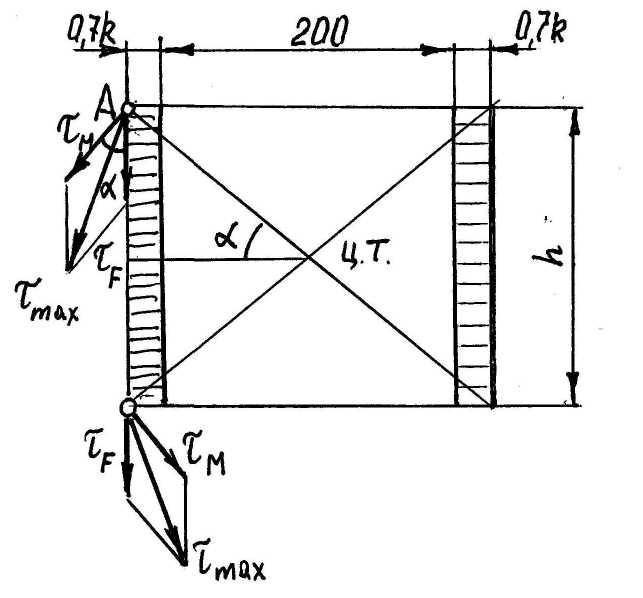
Рис. 2.14

Примем катет шва равным толщине листа k = d = 10 мм. Наибольшие напряжения _max действуют в точке “а” (см. рис. 2.14), где взаимодействуют максимальные напряжения _{max М} от изгибающего момента и касательные напряжения среза от силы F в плоскости шва. Результирующие напряжения в точке “а”

или .

Здесь [] допускаемые напряжения для углового шва. Если сварка выполнена электродом Э – 42 вручную, то по табл.1.1

[] = 0,6 [s_Р] = 0,6171,5 = 102,9 Мпа.

Напряжения от изгибающего момента

.

Здесь максимальный радиус _max =,

Полярный момент инерции двух швов относительно центра тяжести

.

I_X и I_Y осевые моменты инерции относительно горизонтальной (Х) и вертикальной (Y) осей, проходящих через центр тяжести швов.

,

.

напряжения среза в шве от силы F, действующие на одну пластину

где площадь среза для одного шва (см. рис. 2.14)

А_СРЕЗА = 0,7kh = 0,7×10×110 = 770 мм².

Результирующие касательные напряжения в точке “A”

=

Здесь tg = h/0,5a = 55/100 = 0,55;  = 28,8⁰, а – высоты швеллера.

Ответ. Размеры h = 110 мм, d = 10 мм.

Задача №6.

Рассчитать сварное соединение блока со швеллером (рис. 2.15). сила F = 10 кН. Расстояние от центра блока до швеллера h = 300 мм, толщина пластины d = 10 мм. Угол наклона действующей силы  = 30⁰.

Решение.

Рис. 2. 15

1. Определяем размеры сечения П – образного основания блока (рис. 2.16). Толщина его сечения d =10 мм. Ширину “b” сечения определим из условия прочности боковых пластин при изгибе с учётом растяжения. На каждую боковую пластину основания действует сила F, раскладываем ее на две составляющие F₁ и F₂, т.е.

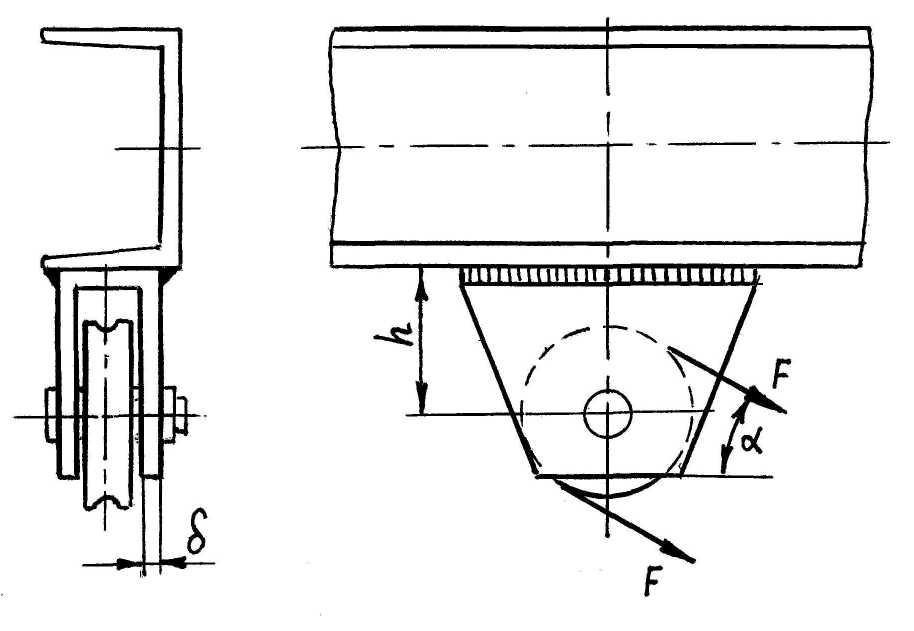
где .

.

С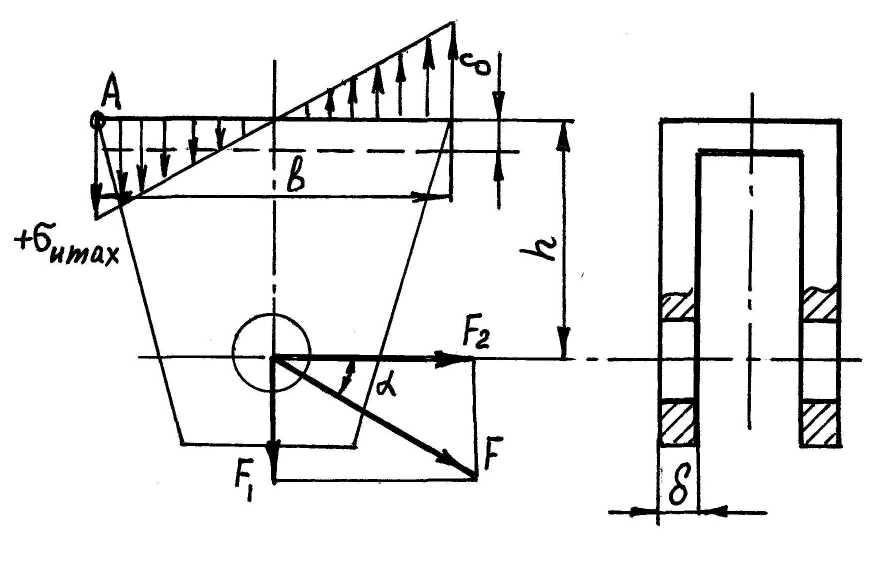 ила F₁ вызывает растягивающие напряжения в пластине, а сила F₂ –

Рис. 2.16

напряжения изгиба у основания пластины. Максимальные напряжения от изгиба возникают в точке “а”, где суммируются с напряжениями растяжения(σ_Р) от силы F₁.

σ_а = σ_{И MAX} + σ_Р.

Максимальные напряжения от изгиба

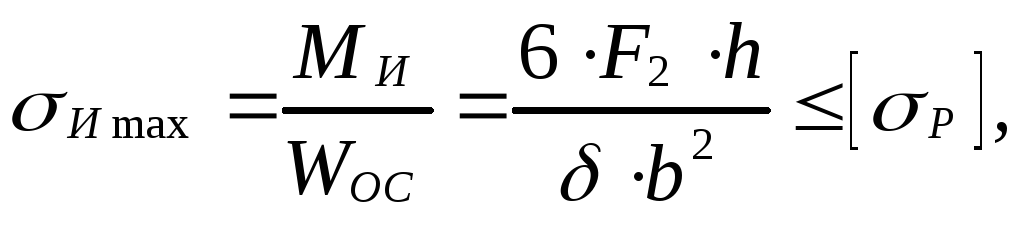
где W_ОС – осевой момент сопротивления сечения пластины (см. рис. 2.16)

Напряжения растяжения в каждой пластине

.

Условие прочности пластины

Принимаем, что основание блока изготовлено из стали 20 с термообработкой – нормализация (_Т = 250 МПа). Тогда допускаемые напряжения

,

где [S] – коэффициент запаса прочности ([S] = 1,8).

Решая уравнение для σ_а, получим

140b² - 500b - 1558800 = 0, или b² - 3,57b – 11134,3 = 0 .

b₁ = 107,3 мм.

Принимаем b = 110 мм.

Проверяем условие прочности по формуле

Условие прочности выполняется.

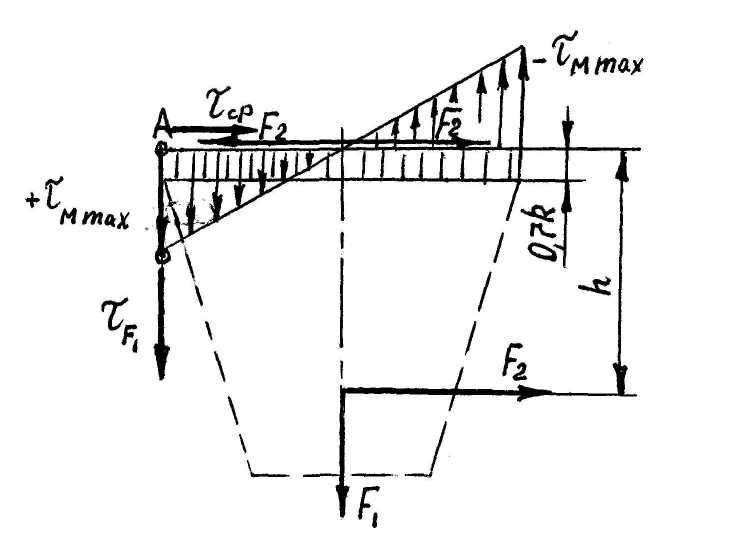
Рис. 2.17

2. Проводим расчет сварного соединения, которое выполнено двумя угловыми швами вдоль стороны “b” основания. Длину каждого шва принимаем равной ширине пластины П–образного основания b = 110 мм. Катет шва принимаем равным толщине пластины k = d = 10 мм. В шве под действием силы F возникают касательные напряжения среза  (рис. 2.17). Силу F₂ переносим в плоскость действия напряжений среза и в центре тяжести двух сечений шва прикладываем статический “ноль” от силы F₂. Расчет ведем по одному шву. В сварном шве от силы F₂ возникают напряжения среза t_СР. Напряжения от момента силы F₂ на плече h вызывают напряжения t_М, которые распределяются неравномерно по длине шва. Закон их распределения аналогичен закону распределения напряжений изгиба σ_И в пластине основания (см. рис. 2.17). Максимальные напряжения t_{МАХ М} будут действовать в точке “a”. Сила F₁ вызывает напряжения среза в шве, которые направлены также как и напряжения t_М.

Результирующие напряжения в шве равны

 t_max =  t_{max М} + ,

Условие прочности шва

Максимальные напряжения от момента

,

где осевой момент сопротивления шва

.

Условие прочности шва не выполняется, т. к. t_{max М} > [t]¢. Здесь [] допускаемые напряжения для углового шва. Если сварка выполнена электродом Э – 42 вручную, то по табл. 1.1

[] = 0,6 [s_Р] = 0,6140 = 84 Мпа.

Пренебрегая напряжениями среза t_F определим длину шва из его условия прочности t_{max М} = [].

.

Откуда

Ширина пластины “b” равная длине шва

.

Увеличиваем ширину пластины “b”и принимаем b = 180 мм.

Максимальные напряжения от момента

напряжения среза в шве от силы F₂, действующие на одну пластину

где площадь среза для одного шва (см. рис. 2.17)

А_СРЕЗА = 0,7kb = 0,7×10×180 = 1260 мм².

Напряжения растяжения в шве от силы F₁

.

Определяем максимальные напряжения в шве и проверяем условие прочности

МПа= 84 МПа

Ответ. Размеры: катет шва k = 10 мм, длина шва (ширина основания) b = 180 мм.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Иванов, М.Н. Детали машин [Текст]: учеб. для студ. ВТУЗов / М. Н. Иванов, В. А. Финогенов. – 10-е изд., испр. - М. : Высш. шк., 2006. – 407 с.

2. Любошиц М. Н., Ицкович Г. М. Справочник по сопротивлению материалов. – 2-е, изд.. испр. . Минск, Вышэйш. школа, 1969. 464 с.

3. Чернавский, С.А. Проектирование механических передач [Текст] учеб.– справ. пособие для втузов/, С.А. Чернавский, Г.А. Снесарев, Б.В. Козинцов и др. М.: Машиностроение, 1984.-560с.

Составители: Сергей Львович Лебский

Михаил Маркович Матлин

Анатолий Александрович Тетюшев