
- •§1. Функция, основные понятия.
- •§2. Основные свойства функций. Четность
- •Периодичность
- •§3. Предел функции. Раскрытие простейших неопределенностей.
- •§4. Сравнение бесконечно малых функций.
- •Говорят, что бесконечно малая a(X) имеет порядок k по сравнению с бесконечно малой b(X) при , если имеют одинаковый порядок малости бесконечно малые a(X) и (b (X))k, то есть
- •Дополнительные упражнения
- •Ответы.
- •§5. Замечательные пределы. Эквивалентные бесконечно малые функции.
- •§6. Односторонние пределы.
- •§7. Непрерывность функции в точке. Точки разрыва.
- •§8. Производная. Правила и формулы дифференцирования.
- •§9. Дифференциал функции, его применение.
- •§10. Дифференцирование неявных и параметрически заданных функций.
- •§11.Геометрический и механический смысл производной.
- •Пример 3
- •Из уравнения первой параболы получаем
- •Дополнительные упражнения
- •§12. Производные высших порядков.
§10. Дифференцирование неявных и параметрически заданных функций.
Пусть уравнение
![]() определяет переменную
определяет переменную
![]() как неявную функцию от переменной
как неявную функцию от переменной
![]() (будем считать эту функцию дифференцируемой).
Тогда для нахождения производной
(будем считать эту функцию дифференцируемой).
Тогда для нахождения производной
![]() нужно продифференцировать обе части
уравнения
нужно продифференцировать обе части
уравнения
![]() по
по
![]() ,
считая при этом, что
,
считая при этом, что
![]() зависит
зависит
![]() ,
и из полученного уравнения, линейного
относительно
,
и из полученного уравнения, линейного
относительно![]() ,
найти производную.
,
найти производную.
Пример 1.
Найти производные
функций
![]() ,
заданных неявно следующими уравнениями: а)
,
заданных неявно следующими уравнениями: а)
![]() , б)
, б)![]() .
.
Решение.
а) Дифференцируем
обе части данного уравнения по
![]() ,
считая
,
считая
![]() :
:
![]()
![]()
![]() .
.
Слагаемые с
![]() оставляем в левой части равенства, общий
множитель
оставляем в левой части равенства, общий
множитель
![]() выносим за скобки и находим
выносим за скобки и находим
![]() как решение линейного уравнения:
как решение линейного уравнения:
![]()
![]()
![]() .
.
Производная неявно
заданной функции получается выраженной
как через аргумент
![]() ,
так и через саму функцию
,
так и через саму функцию
![]() .
Поэтому в ответ ее следует записать
вместе с уравнением, связывающим
.
Поэтому в ответ ее следует записать
вместе с уравнением, связывающим
![]() и
и
![]() .
.
Ответ: ![]() ,
где
,
где
![]() .
.
б) Дифференцируем
обе части данного уравнения по
![]() ,
считая
,
считая
![]() :
:
![]()
![]()
![]() .
.
Слагаемые с
![]() переносим в левую часть равенства, общий
множитель
переносим в левую часть равенства, общий
множитель
![]() выносим за скобки и решаем уравнение
относительно
выносим за скобки и решаем уравнение
относительно
![]() :
:
![]()
![]()
![]() .
.
Ответ:
![]() ,
где
,
где
![]() .
.
Если функция
![]() аргумента
аргумента
![]() задана параметрически:
задана параметрически:
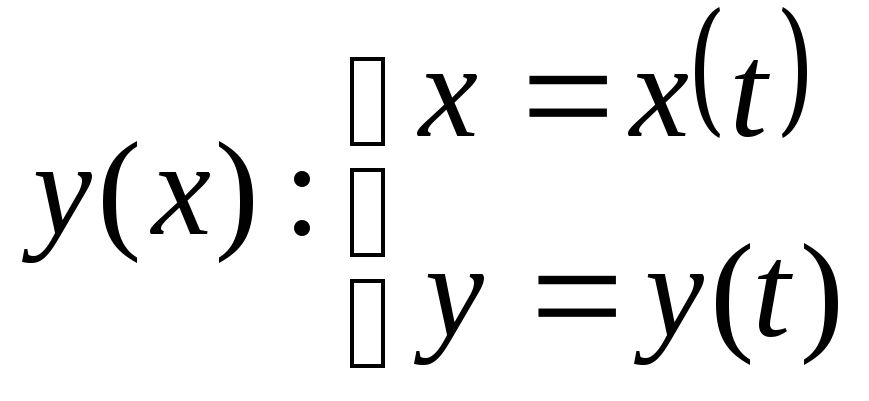 ,
то ее производная вычисляется по
формуле:
,
то ее производная вычисляется по
формуле: ![]() .
.
Пример 2.
Найти производную
![]() функции, заданной параметрически:
функции, заданной параметрически:
а)
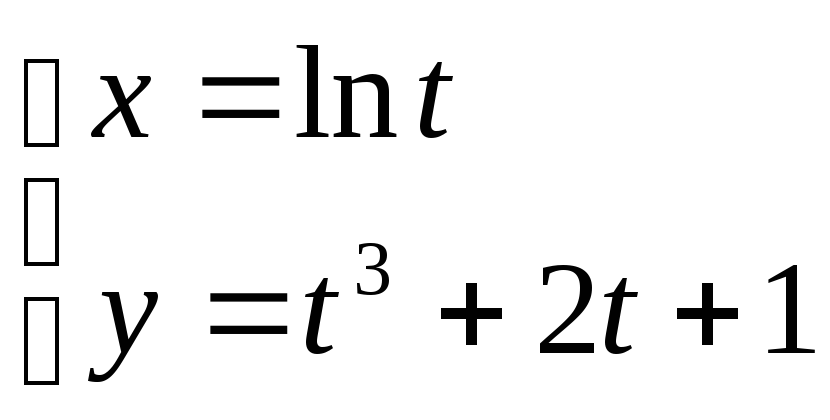 , б)
, б)
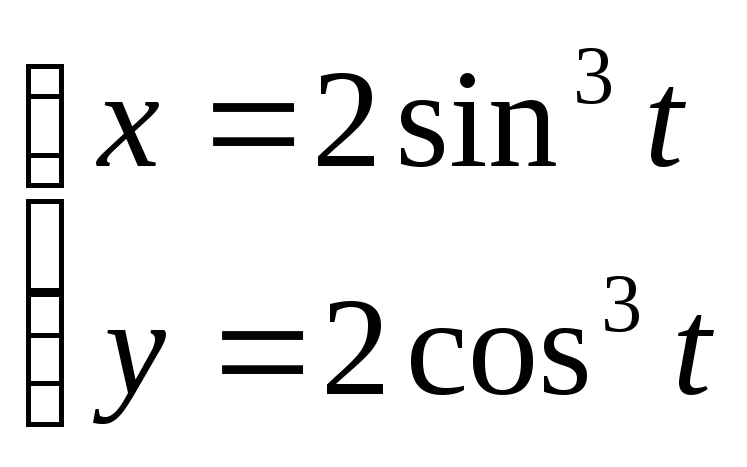 .
.
Решение.
а)
![]() ,
,
![]() .
.
Тогда по формуле
![]() получим
получим
![]()
Производная
![]() получилась выраженной через параметр
получилась выраженной через параметр
![]() .
Как известно, производная функции
.
Как известно, производная функции
![]() является функцией того же аргумента
является функцией того же аргумента
![]() .
Поэтому полученная производная в
рассматриваемом примере должна быть
записана в параметрической форме.
.
Поэтому полученная производная в
рассматриваемом примере должна быть
записана в параметрической форме.
Ответ:
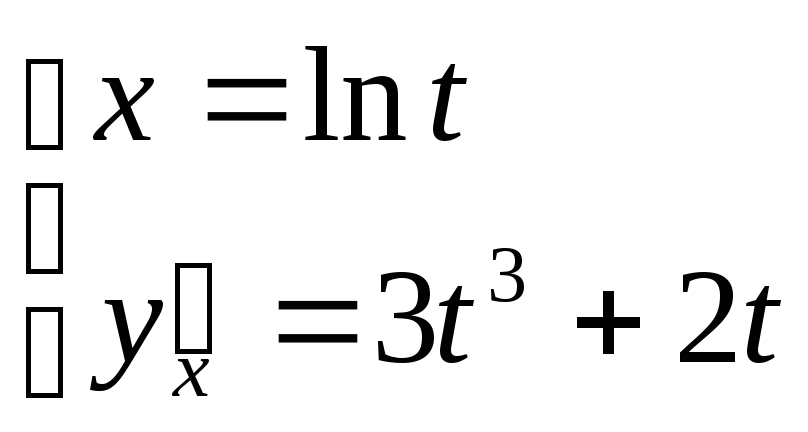 .
.
б) ![]() ,
,
![]() .
.
Тогда по формуле
![]() получим
получим
![]() .
.
Ответ:
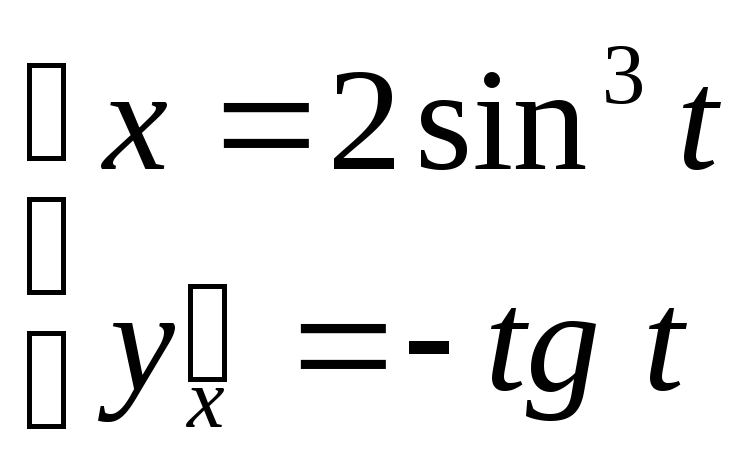 .
.
Самостоятельная работа.
Вариант 1.
а) Найти производную
функции
![]() ,
заданную неявно
,
заданную неявно
![]() .
.
б) Найти производную
![]() функции, заданной параметрически
функции, заданной параметрически
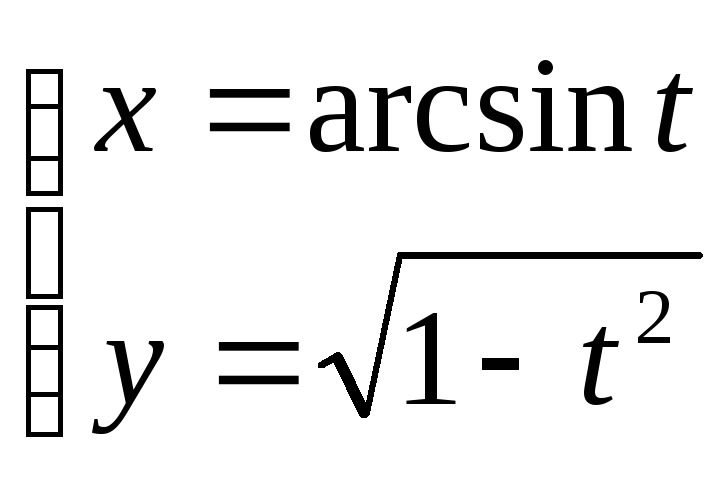 .
.
Вариант 2.
а) Найти производную
функции
![]() ,
заданную неявно
,
заданную неявно
![]() .
.
б) Найти производную
![]() функции, заданной параметрически
функции, заданной параметрически
 .
.
Вариант 3.
а) Найти производную
функции
![]() ,
заданную неявно
,
заданную неявно
![]() .
.
б) Найти производную
![]() функции, заданной параметрически
функции, заданной параметрически
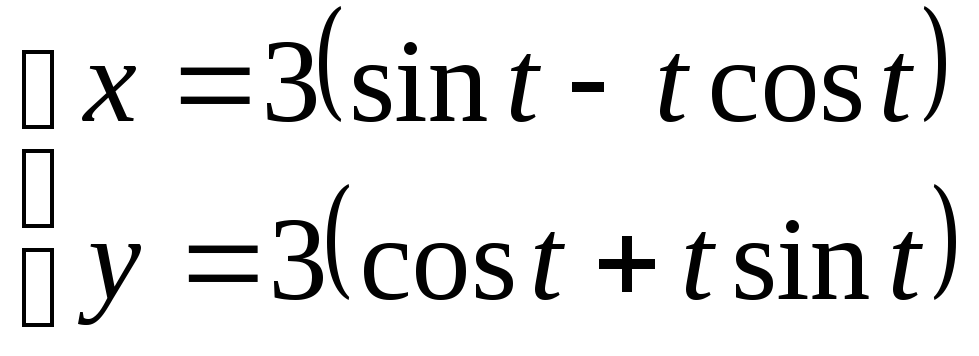 .
.
Ответы.
Вариант 1.
а)
![]() ,
где
,
где
![]() ; б)
; б)
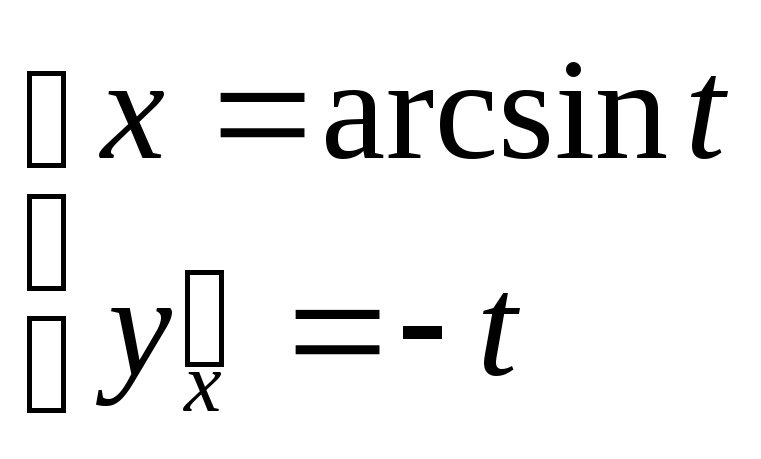 .
.
Вариант 2.
а)
![]() ,
где
,
где
![]() ; б)
; б)
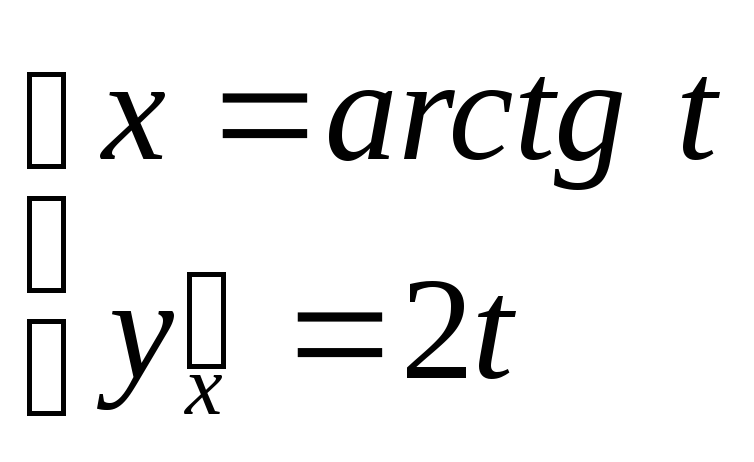 .
.
Вариант 3.
а)
![]() ,
где
,
где
![]() ; б)
; б)
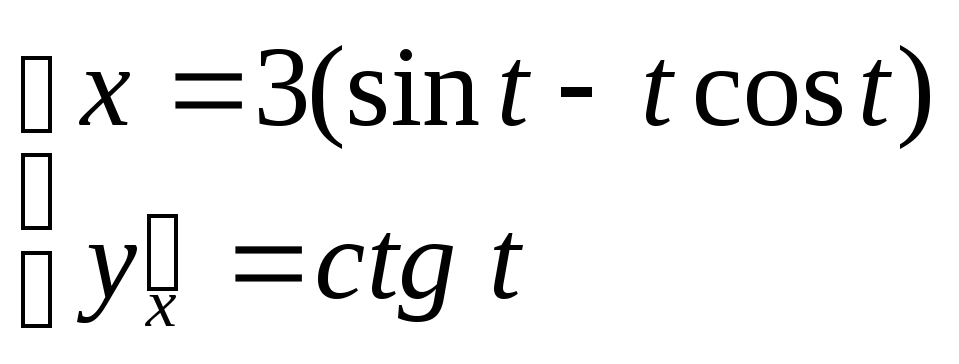 .
.
Дополнительные упражнения.
-
Убедиться в том, что функция
 ,
определяемая уравнением
,
определяемая уравнением
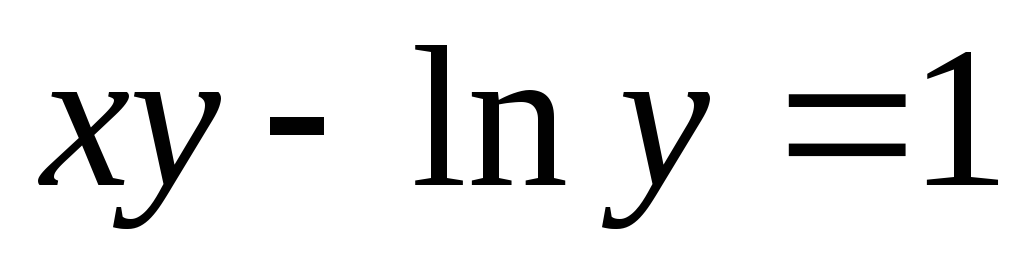 ,
удовлетворяет также соотношению
,
удовлетворяет также соотношению
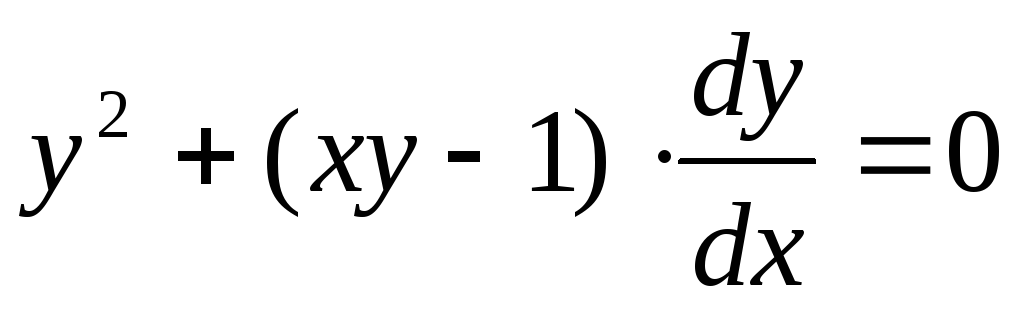 .
. -
Убедиться в том, что функция
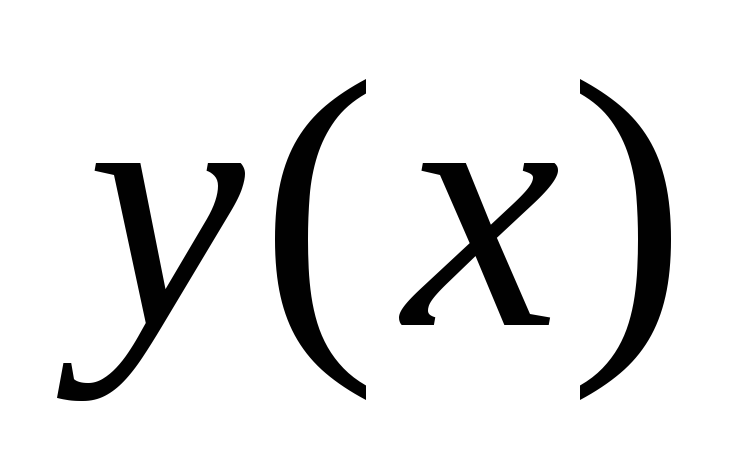 ,
заданная параметрически уравнениями
,
заданная параметрически уравнениями
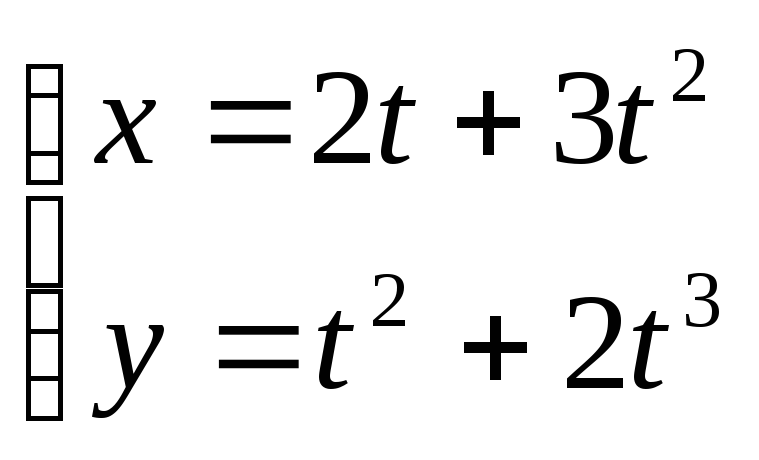 ,
удовлетворяет соотношению
,
удовлетворяет соотношению
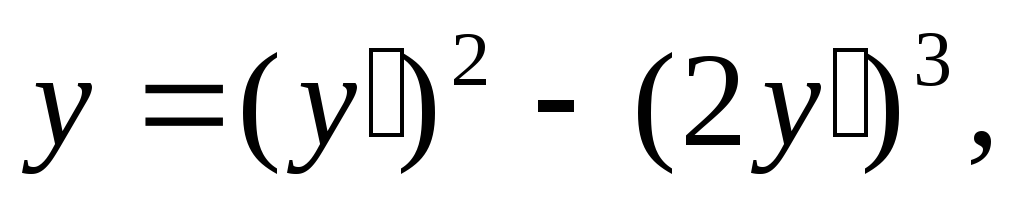 где
где
 .
. -
Убедиться в том, что функция
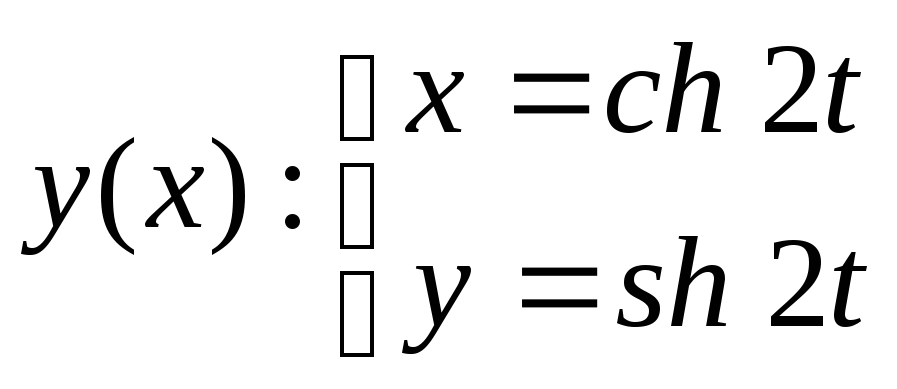 удовлетворяет соотношению
удовлетворяет соотношению
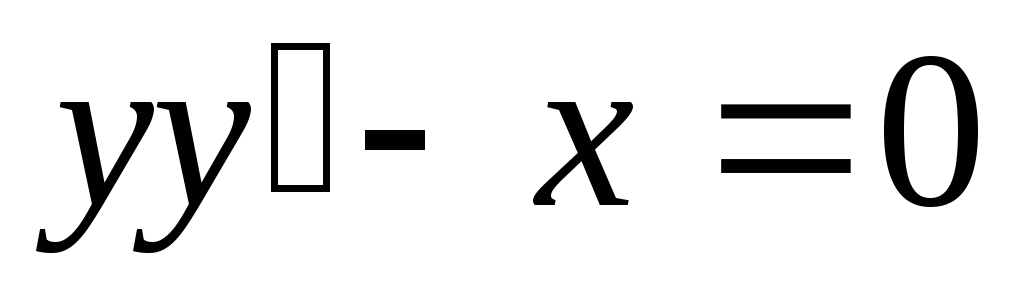 ,
где
,
где
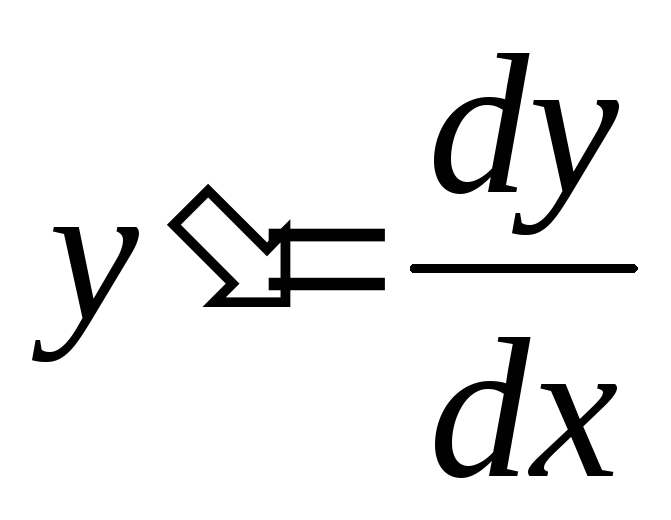 .
.
§11.Геометрический и механический смысл производной.
Если функция
![]() имеет
производную в точке
имеет
производную в точке
![]() ,
то угловой коэффициент касательной к
графику функции в точке
,
то угловой коэффициент касательной к
графику функции в точке
![]() равен
равен ![]() .
.
![]()
Уравнение касательной
к графику функции
![]() в ее точке
в ее точке
![]() имеет вид
имеет вид
![]() .
.
Прямая, проходящая
через точку
![]() и перпендикулярная к касательной,
называется нормалью.
и перпендикулярная к касательной,
называется нормалью.
Если
![]() ,
то уравнение нормали записывается в
виде
,
то уравнение нормали записывается в
виде
![]() .
.
Если
![]() ,
то нормаль имеет уравнение
,
то нормаль имеет уравнение
![]() .
.
Пусть графики
функций
![]() и
и
![]() пересекаются в точке М0.
За угол
пересекаются в точке М0.
За угол
![]() между графиками этих функций принимается
величина меньшего угла, образованного
касательными, проведенными к графикам
в точке М0.
между графиками этих функций принимается
величина меньшего угла, образованного
касательными, проведенными к графикам
в точке М0.
Угол
![]() находится с помощью формулы:
находится с помощью формулы:
![]() ,
,
![]() .
.
Если
![]() ,
то
,
то
![]() .
.
Пример 1.
Под какими углами
синусоида
![]() пересекает ось абсцисс?
пересекает ось абсцисс?
Решение.
Синусоида
![]() пересекает ось абсцисс в точках
пересекает ось абсцисс в точках
![]() ,
,![]() .
.
Ее производная:
![]()
Если
![]() ,
то
,
то
![]() ,
,
то есть угловой
коэффициент касательной к синусоиде
равен единице. Следовательно, в точках
![]() синусоида пересекает ось абсцисс под
углом
синусоида пересекает ось абсцисс под
углом
![]() .
.
Если
![]() ,
то
,
то
![]() ,
,
то есть в этих
точках синусоида пересекает ось абсцисс
под углом
![]() .
.
Ответ:
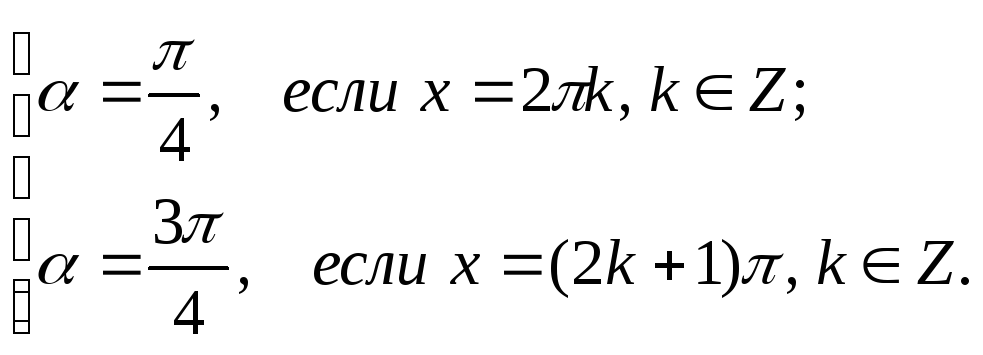
Пример 2.
Написать уравнения
касательной и нормали к графику функции
![]() в точке с абсциссой
в точке с абсциссой
![]() .
.
Решение.
Найдем производную функции:
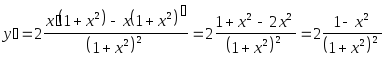 .
.
Вычислим значения
функции и ее производной в точке
![]() :
:
![]() ,
,
![]() .
.
Запишем уравнение касательной
![]()
![]() ,
,
упрощая которое,
получим
![]()
![]()
![]() .
.
Запишем уравнение нормали:
![]()
![]() ,
,
упрощая которое,
получим
![]()
![]() .
.
Ответ: ![]() – уравнение касательной,
– уравнение касательной,
![]() – уравнение нормали.
– уравнение нормали.
