Лабораторная работа № 4

Изучение релексационных процессов в rc-цепи

Цель работы: изучение зависимости тока и напряжения от времени в цепях, содержащих RC-элементы.

Приборы и материалы: универсальный лабораторный стенд, осциллограф, омметр, сменная плата, соединительные провода со штекерами.

1. Краткая теория Теория релаксационного процесса в rc-цепи

RC-цепью называют цепь, содержащую конденсатор и резисторное сопротивление. Под релаксационным процессом в RC-цепях понимается процесс установления стационарного заряда конденсатора при подаче на него напряжения.

Для анализа процесса рассмотрим цепь, приведенную на рис. 4.1.

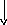
Пусть конденсатор предварительно заряжен зарядом , как показано на рис. 4.1. После замыкания ключа конденсатор начнет разряжаться током , протекающим через резистор . Поскольку емкость и резистор включены параллельно, напряжение на них одно и то же:

. (4.1)

Так как и , то из (4.1) получаем:

. (4.2)

Ток в цепи пропорционален заряду конденсатора . Опираясь на этот факт, можно найти зависимость заряда конденсатора от времени. С течением времени заряд конденсатора уменьшается до нуля, причем скорость уменьшения заряда равна силе тока через конденсатор:

. (4.3)

Пусть время, за которое заряд конденсатора уменьшится в раз, равно . Обозначим за значение тока в цепи в момент времени , а – заряд конденсатора в тот же момент времени. Тогда для момента времени имеем уравнение:

. (4.4)

Это уравнение, с точностью до обозначений, совпадает с уравнением (4.2), поэтому заряд уменьшится в раз через тот же промежуток времени . Продолжая рассуждения, по аналогии можно составить такую таблицу:

Таблица 4.1

	0		2	...
				...

Из таблицы можно заключить, что зависимость заряда конденсатора от времени должна иметь вид:

. (4.5)

Значение , очевидно, равно заряду конденсатора в момент времени , т.е. немедленно после замыкания ключа .

В справедливости полученной формулы легко убедиться, если из уравнения (4.2) исключить силу тока с помощью уравнения (4.3). Уравнение для заряда будет выглядеть так:

. (4.6)

Подставляя из уравнения (4.5), получим:

. (4.7)

Отсюда следует, что уравнения (4.7) и (4.6) удовлетворяются, если:

. (4.8)

Величина называется постоянной времени -цепи.

Зная заряд на конденсаторе, легко найти напряжение на нем, поделив заряд конденсатора на величину его емкости .

Напряжение на конденсаторе меняется по закону:

, (4.9)

где – значение напряжения на конденсаторе при .

Поделив напряжение на величину резисторного сопротивления, можно найти зависимость тока в цепи от времени:

. (4.10)

Графики зависимостей силы тока и напряжения от времени приведены на рис. 4.2 и рис. 4.3.

П

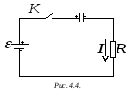одобным образом можно найти зависимости тока и напряжения и для случая зарядки конденсатора в схеме, приведенной на рис. 4.4.

Пусть до замыкания ключа конденсатор не заряжен. После замыкания ключа в момент времени в цепи возникает ток , и конденсатор начинает заряжаться. При этом для контура выполняется второй закон Кирхгофа:

. (4.11)

Заменив и , получаем:

. (4.12)

Так как сила тока равна скорости увеличения заряда конденсатора:

, (4.13)

то, дифференцируя (4.12) и подставляя из (4.13), получаем:

. (4.14)

Уравнение (4.14) совпадает с точностью до замены на с уравнением (4.6). Поэтому решение уравнения (4.14) можно написать по аналогии с решением уравнения (4.6):

, (4.15)

где – значение тока в начальный момент времени, которое можно определить из уравнения (4.11), учитывая, что при . Тогда:

, (4.16)

а напряжение на резисторе меняется по закону:

. (4.17)

Напряжение на емкости можно найти из (4.11) и (4.17):

. (4.18)

Графики этих зависимостей приведены на рис. 4.5 и рис. 4.6.