СПИСОК

1. Лекция № 8

«Вычислительные приемы сложения и вычитания для чисел первой сотни».

2. Лекция № 9

«Вычислительные приемы сложения и вычитания для чисел первой тысячи и многозначных чисел».

3. Лекция № 10

«Умножение».

4. Лекция № 11

«Деление».

5. Лекция № 12

«Особые случаи умножения и деления».

Вычислительные приемы сложения и вычитания для чисел первой сотни вычислительные приемы сложения и вычитания для чисел первой сотни

1. Используемые математические законы и правила.

2. Способы устных вычислений.

3. Способы письменных вычислений.

Используемые математические законы и правила

1. Используемые математические законы и правила.

ПРАВИЛО ГРУППИРОВКИ СЛАГАЕМЫХ

Правило группировки слагаемых играет роль вычислительного приема, позволяющего рационализировать вычислительную деятельность. Это правило может быть использовано при выполнении действий в выражениях, содержащих двух слагаемых. При этом обязательно следует отметить, что это правило касается только выражений, содержащих действие сложения. Правило изучается во 2 классе.

Правило группировки слагаемых:

При сложении трех и более чисел соседние слагаемые можно заменять их суммой.

Вычисли удобным способом:

3+6+4=… 7+30+60=…

90-70+5=… 30+8+30=…

(Легче сначала сложить 6и4 – это 10, затем прибавить к 10 число 3, получится 13.

Легче сначала сложить 30 и 60 – это 90, затем прибавить к сумме 7 – это 97.

Для случая 90 – 70+5 правило группировки слагаемых неприменимо, поскольку это выражение содержит сложение и вычитание. В этом выражении действия надо выполнять по порядку слева направо.

Для случая 30+8+30 легче сначала сложить 30 и 30 – это 60, а затем прибавить к сумме 8 – это 68).

Правило сложения и вычитания разрядных единиц.

Следствием правила группировки слагаемых выступают два следующих правила, определяющих способ сложения и вычитания разрядных единиц:

Единицы складывают с единицами. Десятки складывают с десятками.

Н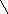апример для случая 56 + 3 = 50 + (6 + 3) = 59

50 6

удобно единицы складывать с единицами;

для случая 60 + 35 = (60 + 30) + 5 = 95

30 5

удобно десятки складывать с десятками.

В обоих случаях одно из слагаемых представлено в виде суммы разрядных слагаемых и выполняется прибавление числа к сумме разрядных слагаемых. В более ранних вариантах учебников математики для начальных классов правило прибавления числа к сумме и правило прибавления суммы к числу изучалось в явном виде (правило сообщалось детям и заучивалось как основа вычислительного приема).

Первое правило звучало так:

Чтобы прибавить число к сумме, можно прибавить его к любому слагаемому,

а затем к полученной сумме прибавить оставшиеся слагаемое.

Второе правило формулировалось так:

Чтобы прибавить сумму к числу, можно прибавлять к этому числу любое слагаемое суммы, а затем к полученному результату прибавить оставшееся слагаемое.

Правила были сочтены громоздкими и их заменили формулировками, сориентированными на поразрядное сложение. Однако для случаев вида 26+7 или 45+16 приходится использовать именно эти правила, а не правила поразрядного сложения.

Аналогичное упрощенное правило вводится для вычитания:

Десятки вычитаются из десятков.

Единицы вычитаются из единиц.

Например, для случая 29 – 3 = 20 + (9 – 3) = 26

20 9

удобно единицы вычитать из единиц;

для случая 56 – 30 = (50 – 30) + 6 = 26

50 6

удобно десятки вычитать из десятков.

Однако для случая вида 30 – 6, 45 – 7, 50 – 24 эти правила приходится неявно заменять на общие правила вычитания числа из суммы и вычитания суммы из числа. Сами правила уже не рассматриваются в последней редакции учебника математики, но использовать их при вычислениях приходится. В связи с этим большая часть вычислительных приемов первой сотни предлагается детям в виде разбора образцов действий, а затем закрепления каждого способа действия на аналогичных примерах. С психологической точки зрения такой путь обучения вычислениям не ведет к становлению обобщенных приемов вычислительной деятельности.

Правило вычитания числа из суммы:

чтобы вычесть число из суммы, можно вычесть это число из любого слагаемого,

а затем к результату прибавить оставшееся слагаемое.

Например: 30 – 6 = 20 + (10 – 6) = 24

20 +10

В данном случае уменьшаемое 30 рассматривается как сумма 20 и 10.

Правило вычитания суммы из числа:

чтобы вычесть сумму из числа, можно вычесть из этого числа любое слагаемое,

А затем из полученного результата вычесть другое слагаемое.

Например: 45 – 7 = (45 – 5) – 2 = 40 – 2 = 38

5 + 2

В данном случае вычитаемое 7 рассматривается как сумма 5 и 2.

Способы устных вычислений.