
- •Оглавление
- •Введение
- •1. Аналитическая геометрия и линейная алгебра.
- •Занятие № 5. Линейные пространства.
- •Занятие № 6. Евклидовы пространства.
- •Занятие № 7. Линейные операторы и матрицы.
- •Занятие № 10. Скалярное произведение векторов.
- •Занятие № 11. Векторное и смешанное произведение векторов.
- •Занятие № 12. Прямая на плоскости.
- •Занятие № 13. Кривые второго порядка.
- •Занятие № 14. Преобразование координат на плоскости. Приведение уравнений к каноническому виду.
- •Занятие № 15. Плоскость в пространстве.
- •Занятие № 16. Прямая в пространстве.
- •Занятие № 17. Взаимное расположение прямых и плоскостей в пространстве.
- •Занятие № 18. Поверхности в пространстве.
- •2. Введение в математический анализ.
- •21.3. Доказать, что последовательность
- •4. Интегральное исчисление функций одной переменной.
- •5. Дифференциальное исчисление функций нескольких переменных.
- •Занятие № 46. Пределы и непрерывность функции нескольких переменных.
- •Занятие № 47. Частные производные и дифференциалы.
- •Занятие № 48. Касательная плоскость и нормаль к поверхности.
- •Занятие № 49. Производная по направлению. Градиент.
- •6. Интегральное исчисление функций нескольких переменных. Занятие № 53. Двойные интегралы.
- •7. Ряды.
- •8. Обыкновенные дифференциальные уравнения.
- •19.1. A); б); в); г). 19.2. А); б); в); г). 19.3. А) четная; б) общего вида; в) нечетная.
- •27.4. Касательная , нормаль . 27.5.
- •Рекомендуемая литература
8. Обыкновенные дифференциальные уравнения.
Занятие № 61.
Уравнения с разделяющимися переменными.
61.1. Решить уравнения:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() ;
з)
;
з)
![]() .
.
61.2. Найти решения, удовлетворяющие начальным условиям:
а)
![]()
![]() ;
б)
;
б)
![]()
![]() ;
;
в)
![]()
![]() ;
г)
;
г)
![]()
![]() .
.
Занятие № 62.
Однородные уравнения.
62.1. Решить уравнения:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
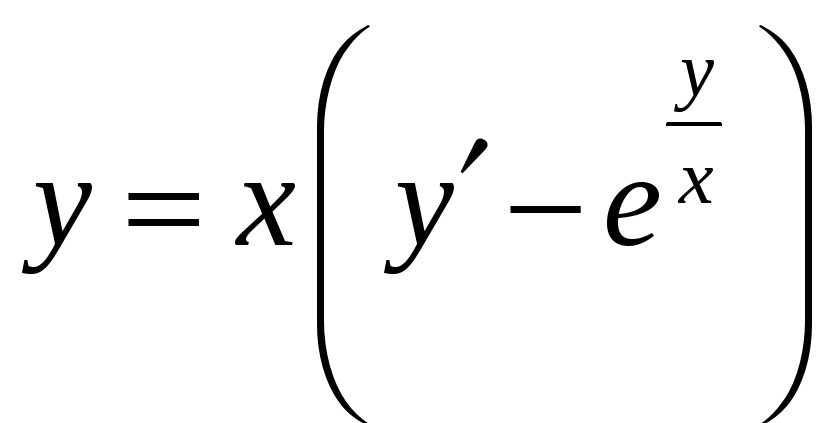 ;
д)
;
д)
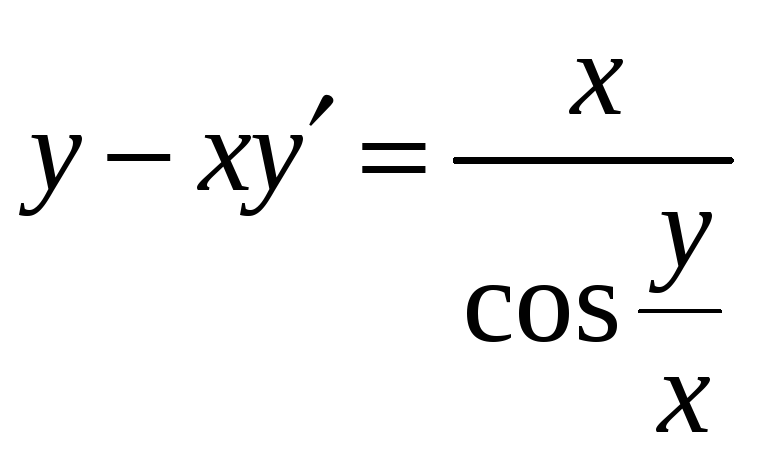 .
.
62.2. Найти решения, удовлетворяющие начальным условиям:
а)
![]() ;
б)
;
б)
![]() .
.
Занятие № 63.
Линейные уравнения первого порядка.
63.1. Решить уравнения:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() .
.
63.2. Найти решения, удовлетворяющие начальным условиям:
а)
![]()
![]() ;
б)
;
б)
![]()
![]() ;
в)
;
в)
![]()
![]() .
.
63.3. Решить уравнения Бернулли:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Занятие № 64.
Уравнения в полных дифференциалах и
не разрешенные относительно производной.
64.1. Решить уравнения в полных дифференциалах:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
64.2. Решить уравнения, не разрешенные относительно производной:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ;
е)
;
е)
![]() ;
ж)
;
ж)
![]() ;
з)
;
з)
![]() .
.
Занятие № 65.
Линейные дифференциальные уравнения
с постоянными коэффициентами.
65.1. Решить однородные уравнения:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
65.2. Решить неоднородные уравнения с правой частью специального вида:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() ;
з)
;
з)
![]() .
.
65.3. Решить уравнения методом вариации постоянных:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Занятие № 66.
Системы дифференциальных уравнений.
66.1. Решить системы уравнений:
а)
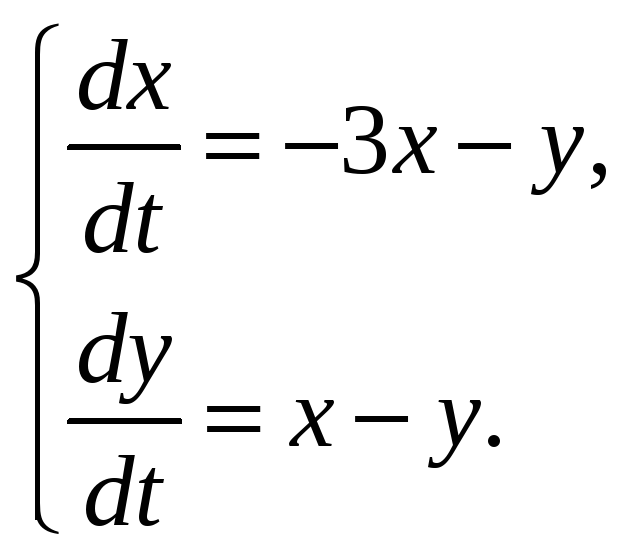 б)
б)
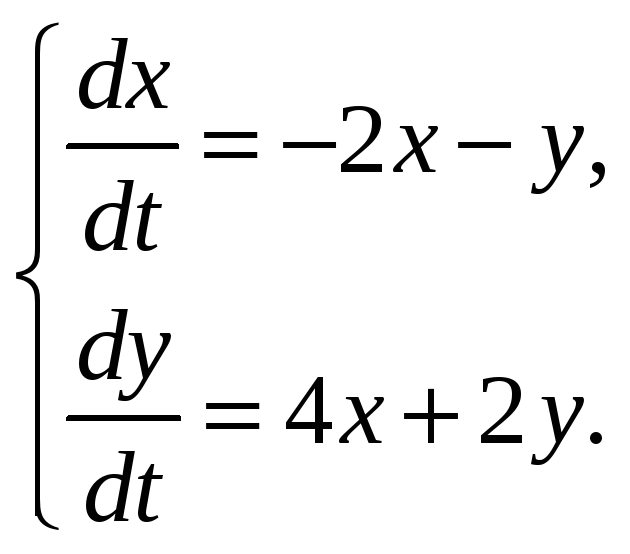
в)
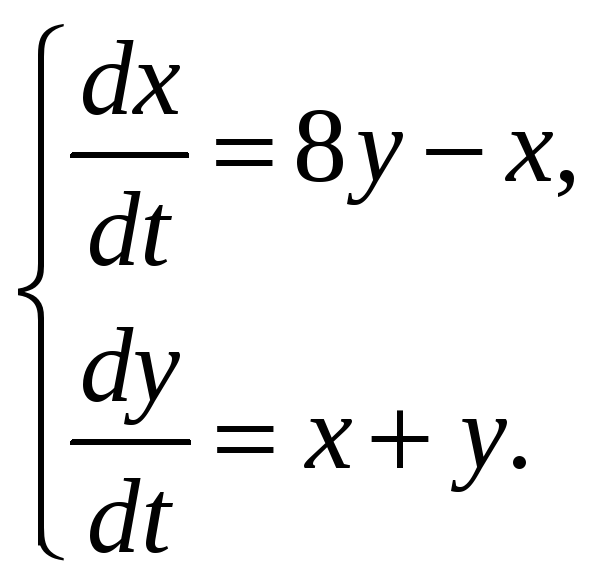 г)
г)
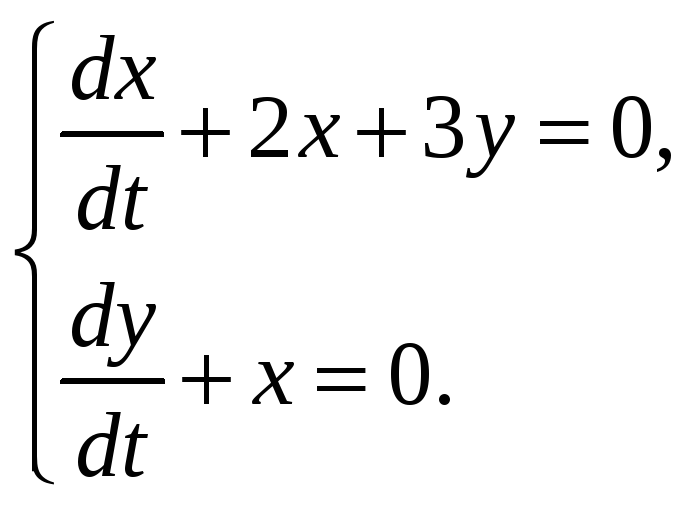
д)
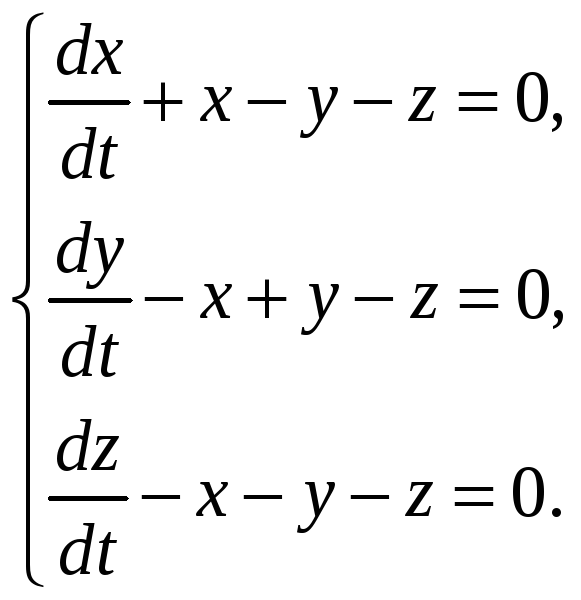 е)
е)
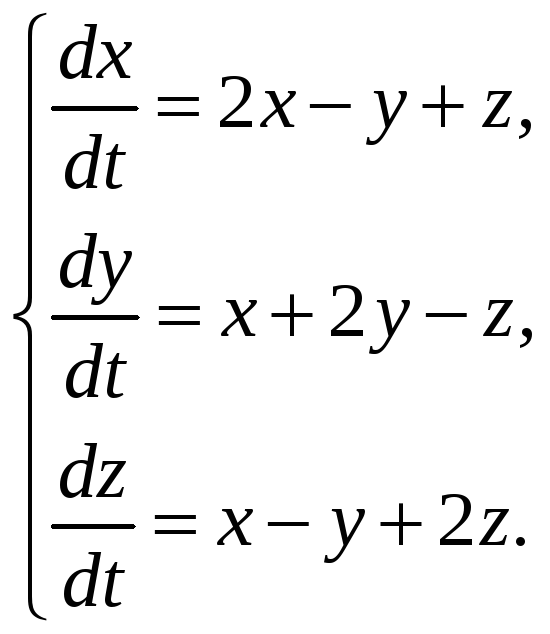
ж)
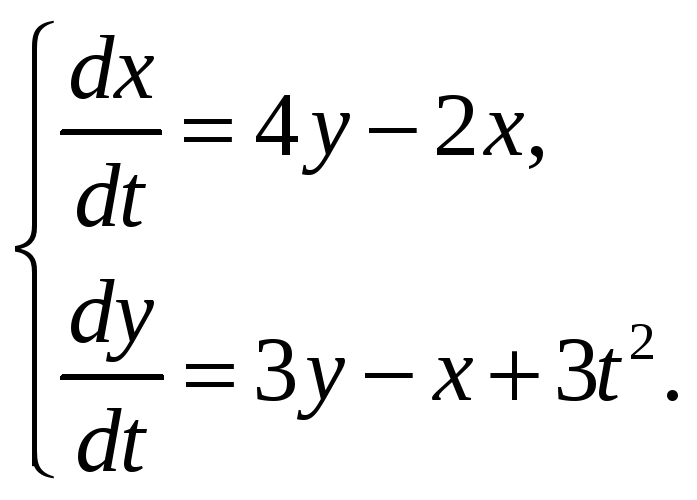 з)
з)
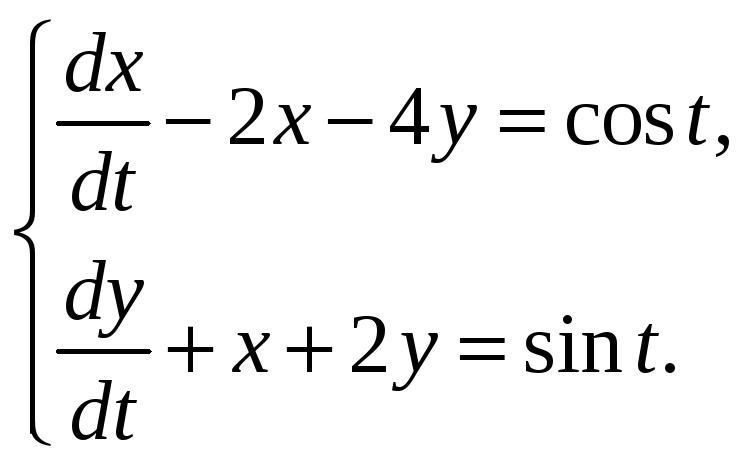
и)
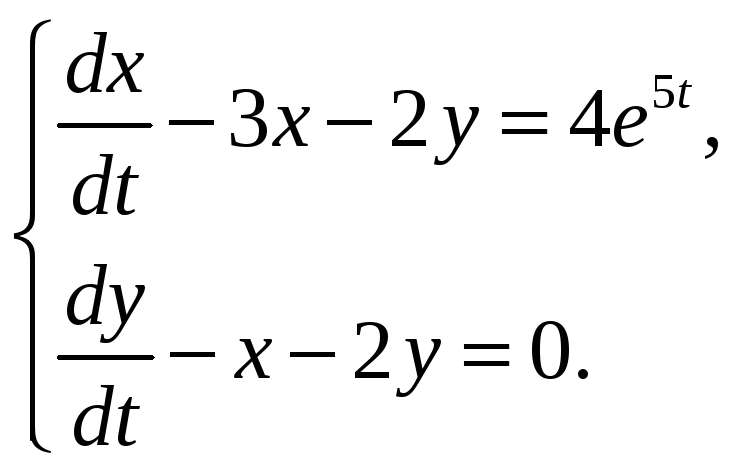 к)
к)
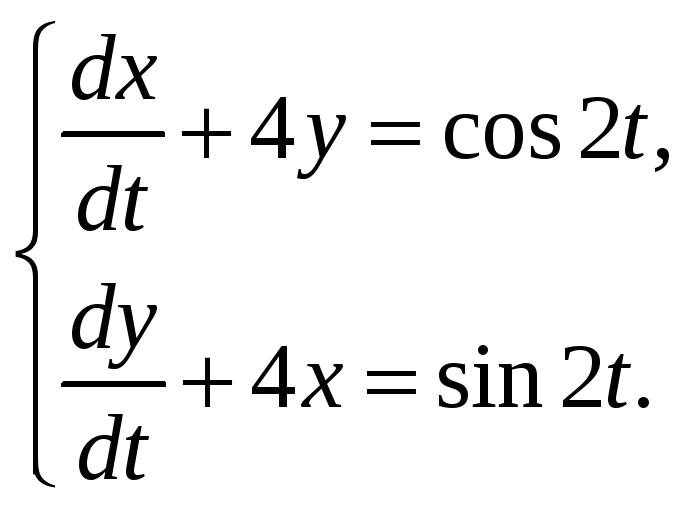
Ответы.
1.1. а)![]() ; б)
; б)
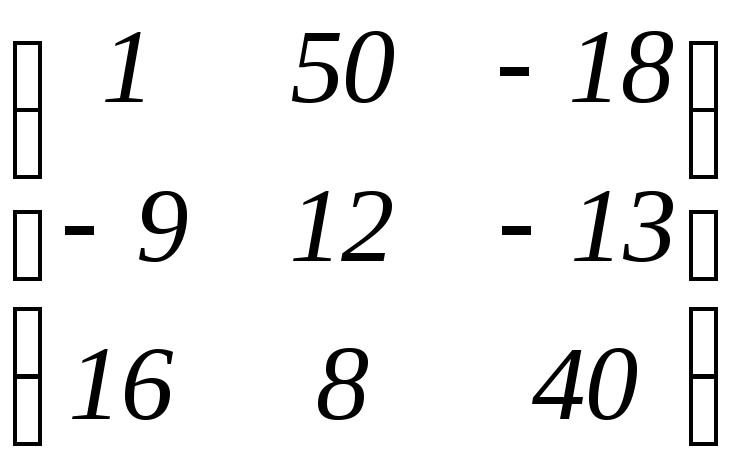 ;
в)
;
в)
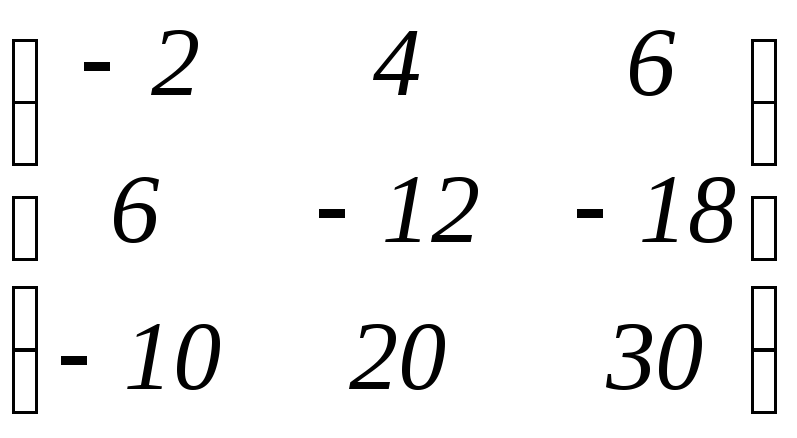 ;
г) -41;
;
г) -41;
д)
 ;
е)
;
е)
 .
1.2. а)
.
1.2. а)
![]() ;
б)
;
б)
![]() .
.
1.3.
а) 1 ; б) 8ab
; в) 0 ; г) 19. 1.4.
а) 1449 ; б) -16 ; в) 0 ; г) -3692. 1.5. а)
![]() ;
;
б)
![]() ;
в)
;
в)
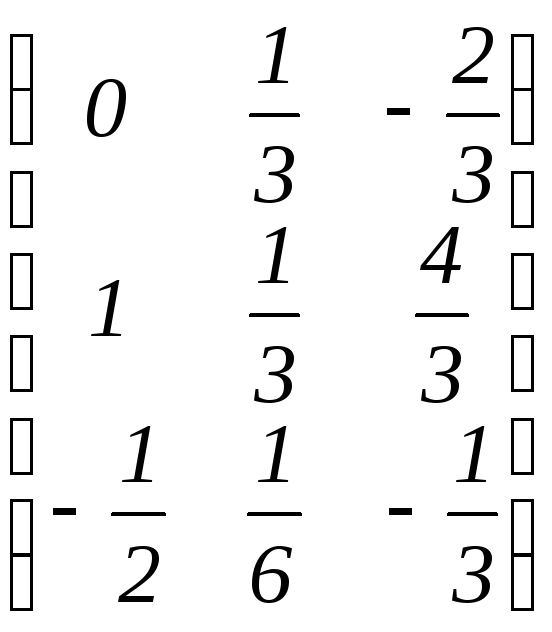 ;
г)
;
г)
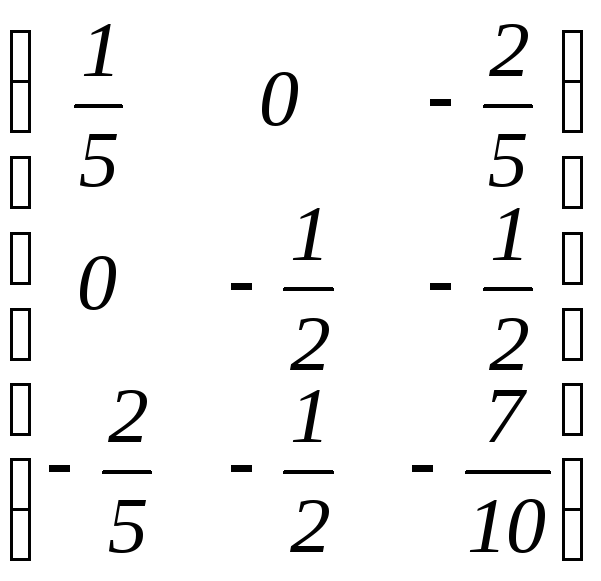 ;
д) необратима;
;
д) необратима;
е)
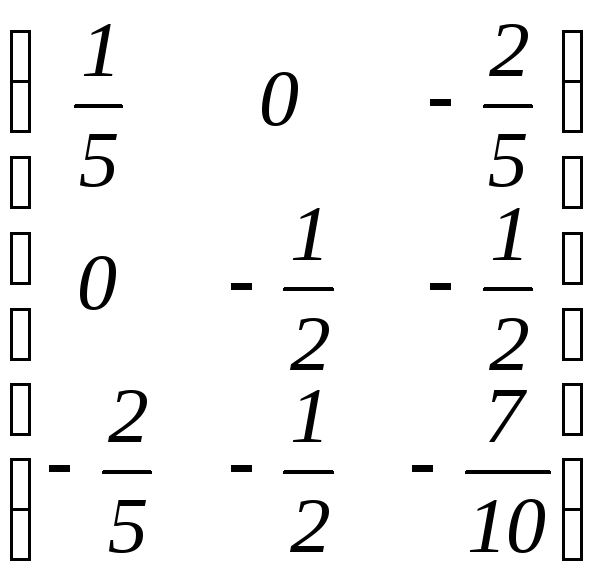 .
.
2.1.
а) 2; б) 3 ; в) 4 ; г) 4. 2.2.
4. 2.3. а)
m=8,
r=3;
б) m=1,
r=3.
2.4. а)
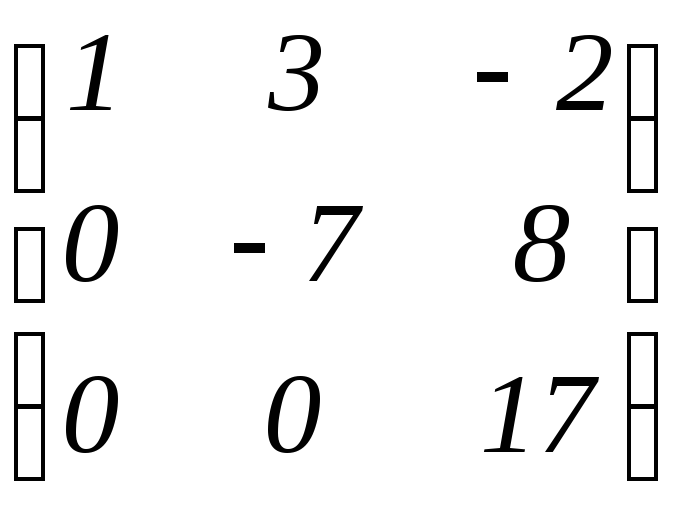 ;
;
б)
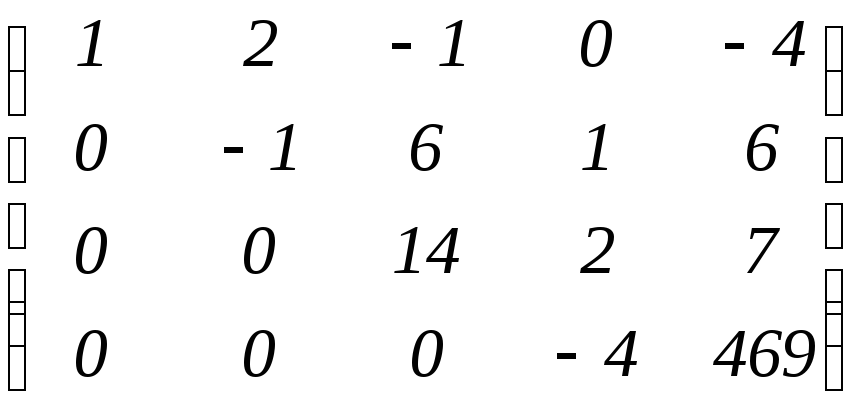 ;
в)
;
в)
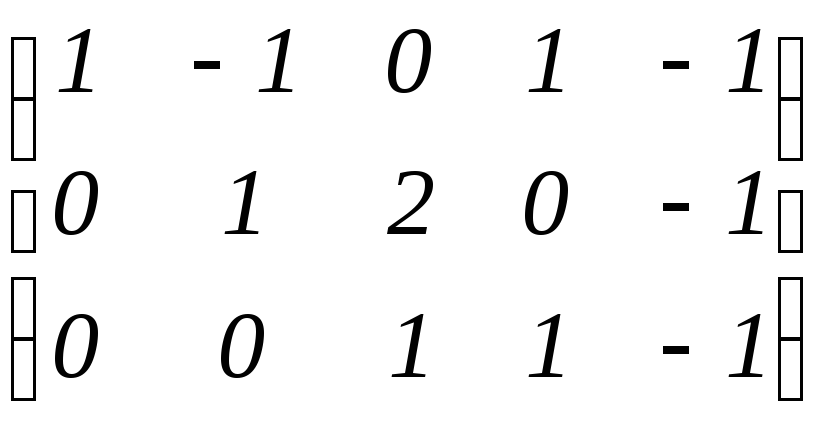 ;
;
г)
![]() .
.
3.1.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
3.2.
а)
![]() ;
б)
;
б)
![]() .
3.3.
а) Решение существует и единственное
.
3.3.
а) Решение существует и единственное
![]() ;
б) Решение отсутствует; в) Существует
бесконечное множество решений
;
б) Решение отсутствует; в) Существует
бесконечное множество решений
![]() .
.
4.1.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
г) Система несовместна;
;
г) Система несовместна;
д)
![]() ;
;
е)
![]() .
.
4.2. а)
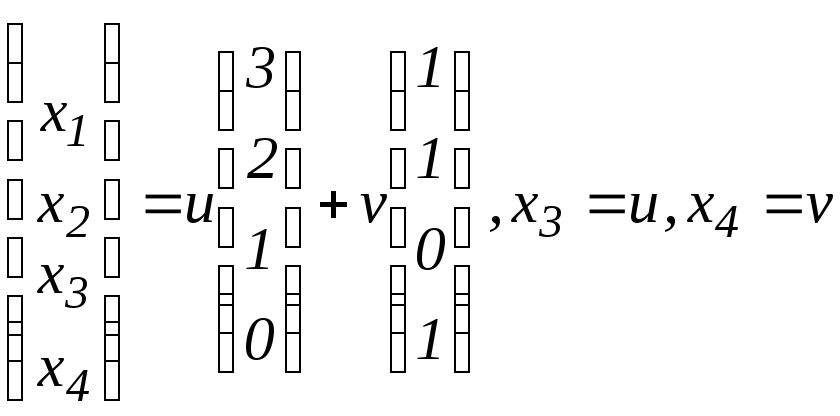 ;
б)
;
б)
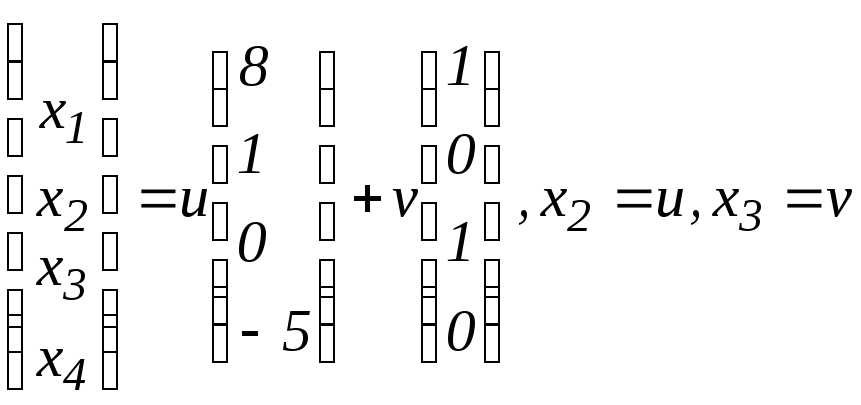 ;
;
в)
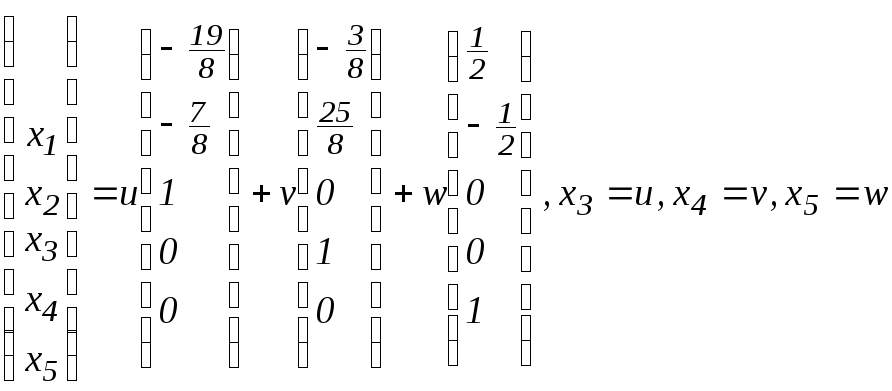 .
.
4.3. а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
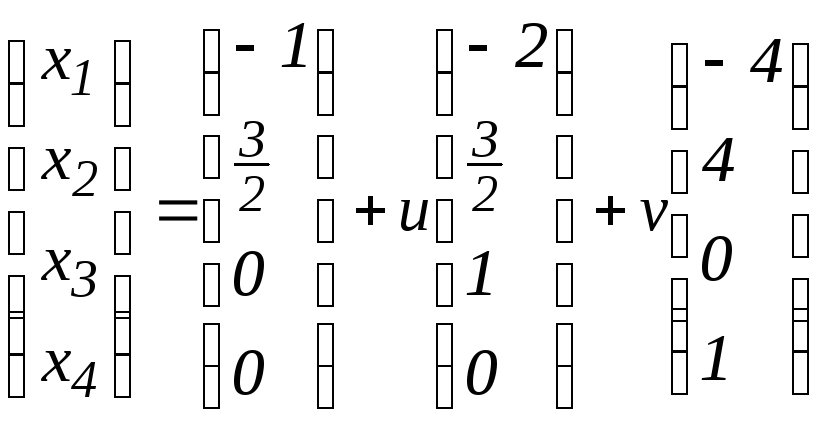 ;
;
д)
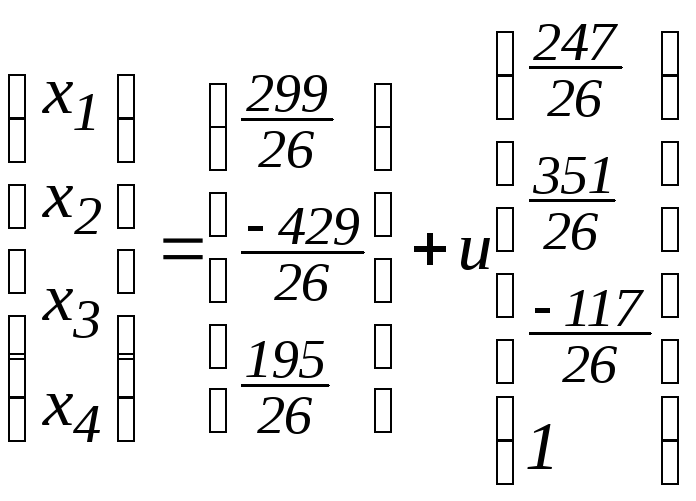 ;
е)
;
е)
![]() ,
система определенная. 4.4.
а)
,
система определенная. 4.4.
а)
![]() ;
;
б)
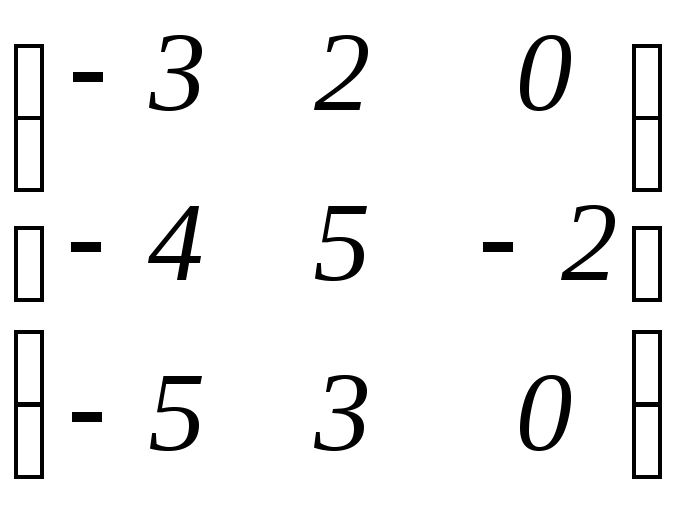 ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
5.1. а)
Да; б) Нет; в) Нет; д) Да. 5.2.
а) 2; б) 4; в) 3. 5.3.
![]() .
5.4.
.
5.4.
![]() .
5.5.
.
5.5.
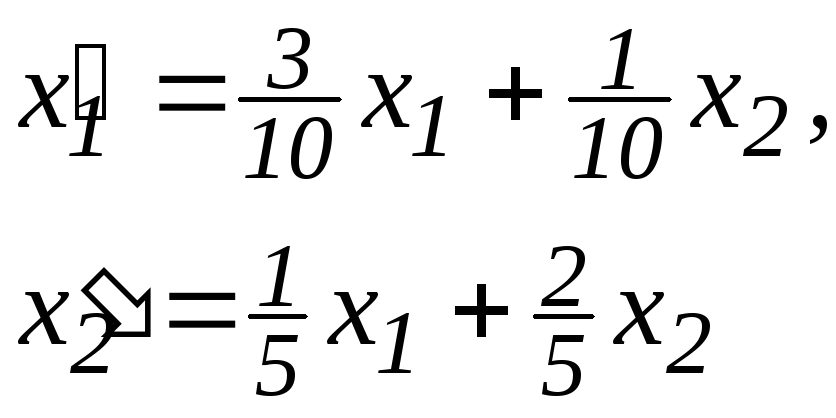 .
5.6.
.
5.6.
![]() .5.7.
а) Размерность равна 3, базис образуют
.5.7.
а) Размерность равна 3, базис образуют
![]() ; б) Размерность равна 3, базис образуют
; б) Размерность равна 3, базис образуют
![]() .
.
5.8.
![]() .
5.9.
.
5.9.
![]() .
.
5.10. а)
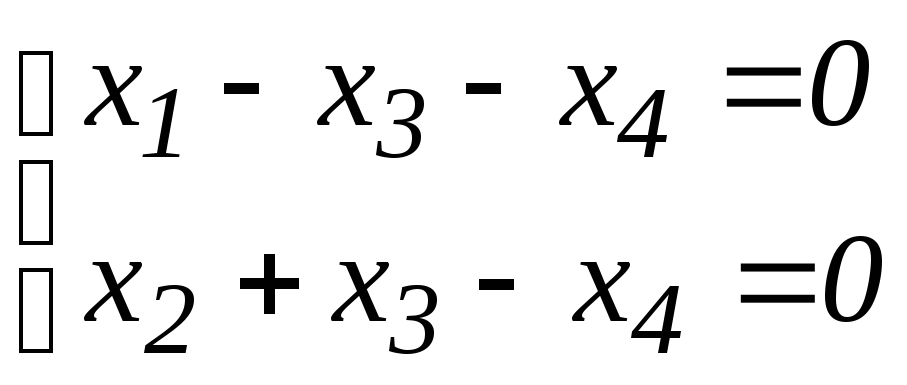 ;
б)
;
б)
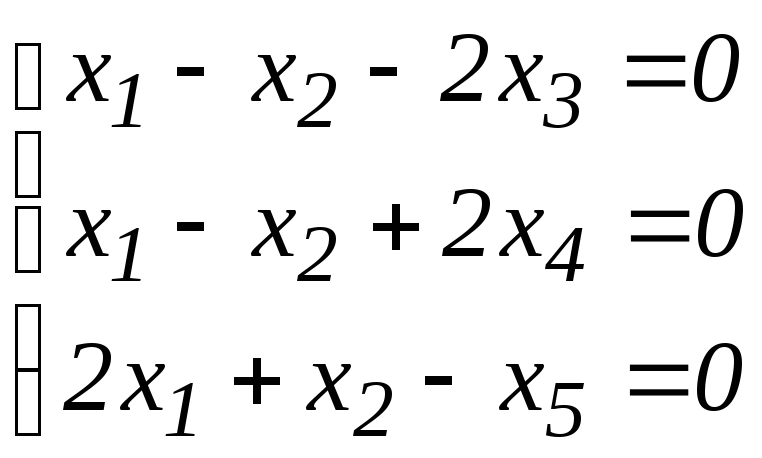 .
.
6.1.
![]() .
6.2.
.
6.2.
![]() .
.
6.3.
а)
![]() ;
б)
;
б)
![]() .
.
6.4.
а)
![]() ;
б)
;
б)
![]()
6.5.
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() .
.
7.1.
![]() .
7.2.
.
7.2.
![]() .7.3.
.7.3.
![]() .
7.4.
.
7.4.
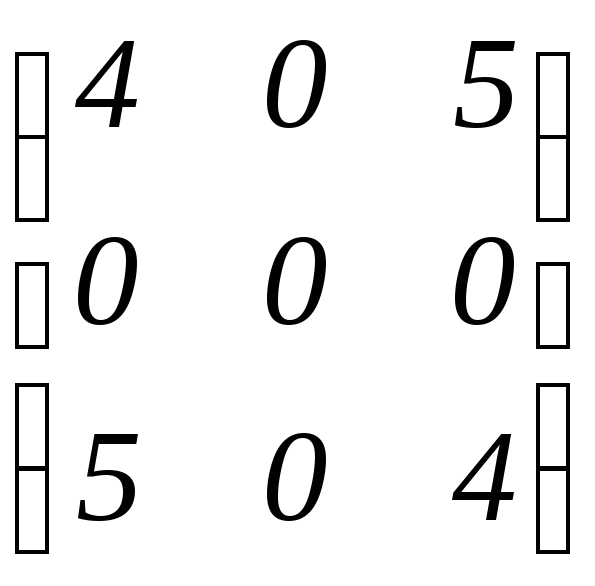 .
.
7.5.
а)
![]() ,
собственные векторы
,
собственные векторы
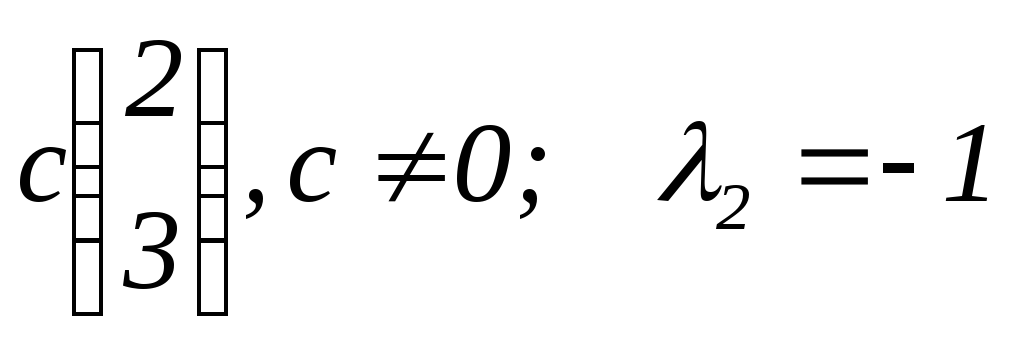 ,
собственные векторы
,
собственные векторы
![]() ;
б)
;
б)
![]() ,
собственные векторы
,
собственные векторы
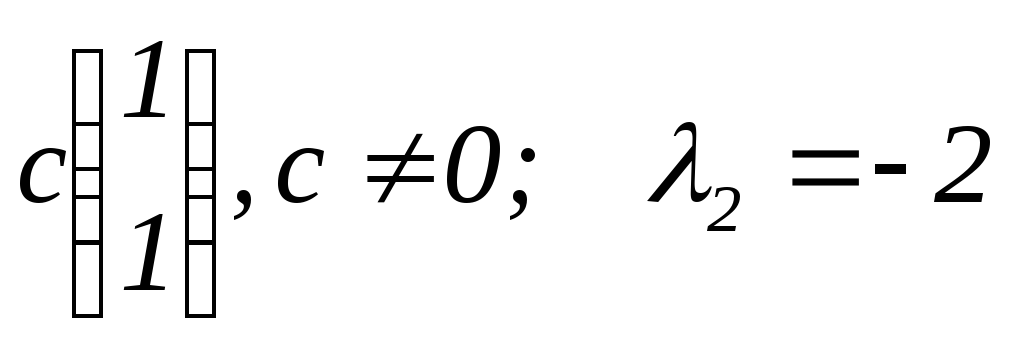 ,
собственные векторы
,
собственные векторы
![]() ;
в)
;
в)
![]() ,
собственные векторы
,
собственные векторы
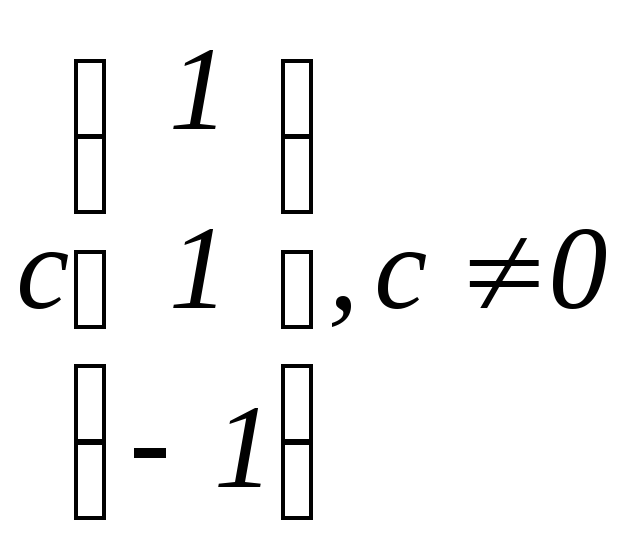 ;
г)
;
г)
![]() ,
собственные векторы
,
собственные векторы
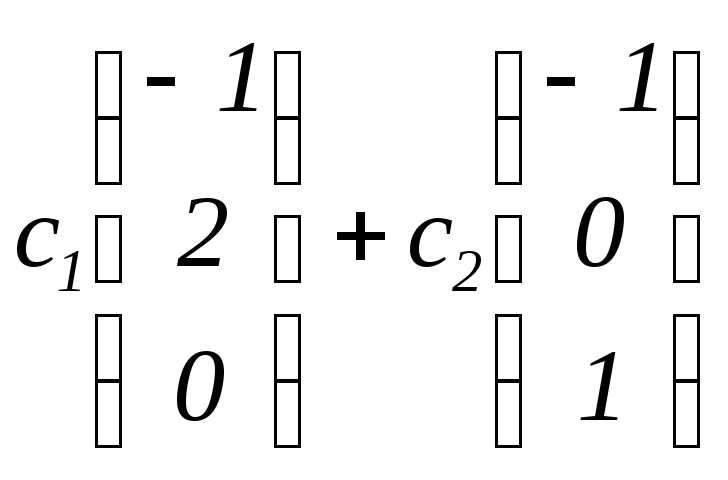 ,
где
,
где
![]() и
и
![]() одновременно;
одновременно;
![]() ,
собственные векторы
,
собственные векторы
![]() ,
где
,
где
![]() ;
д)
;
д)
![]() ,
собственные векторы
,
собственные векторы
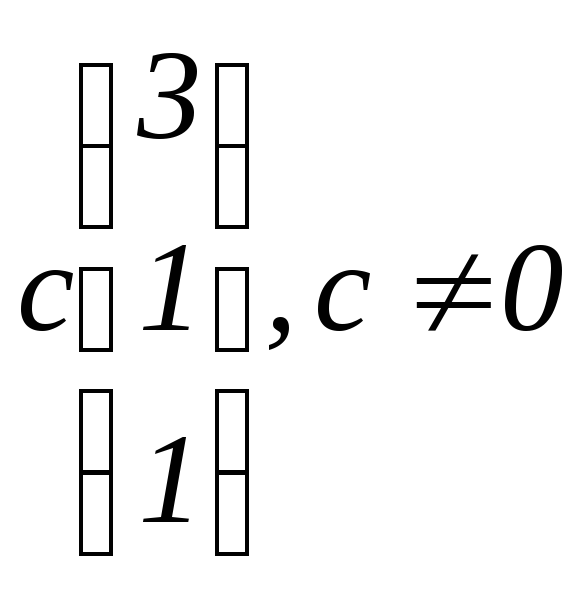 .
8.1.
а)
.
8.1.
а)
![]() ;
б)
;
б)
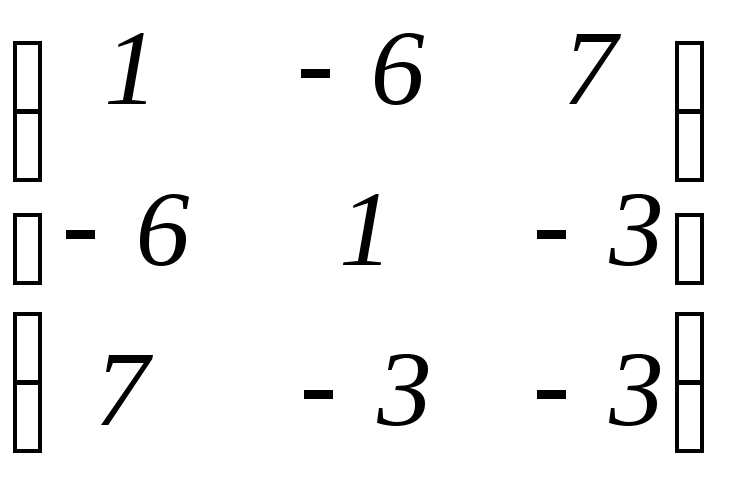 .
.
8.2.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() .
.
8.3.
а)
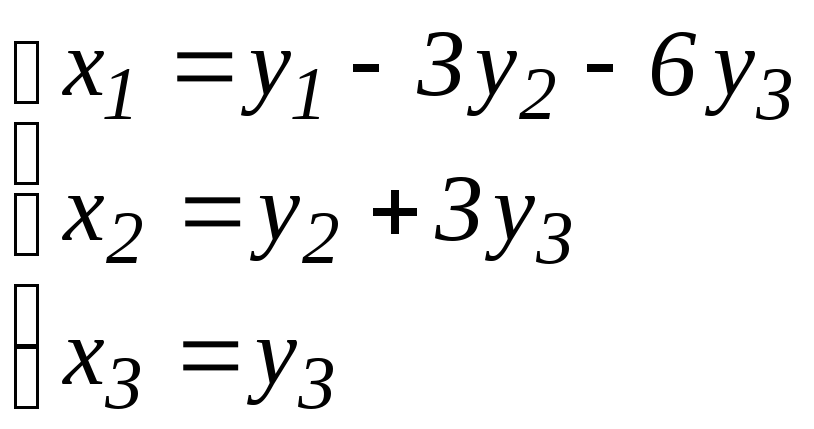 ;
б)
;
б)
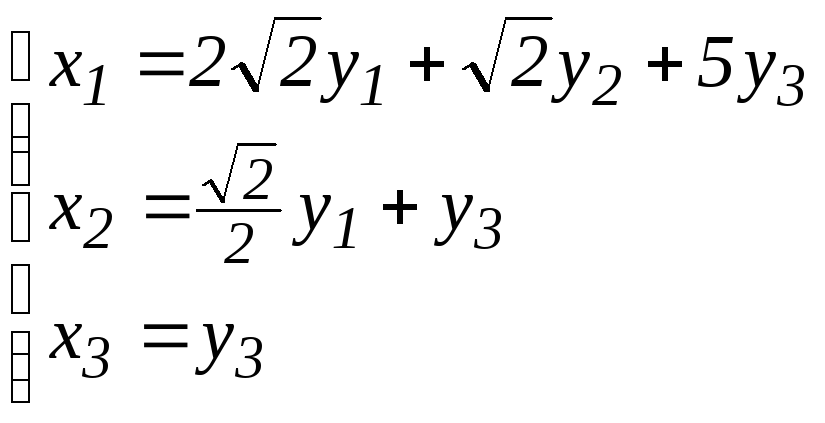 ;
;
в)
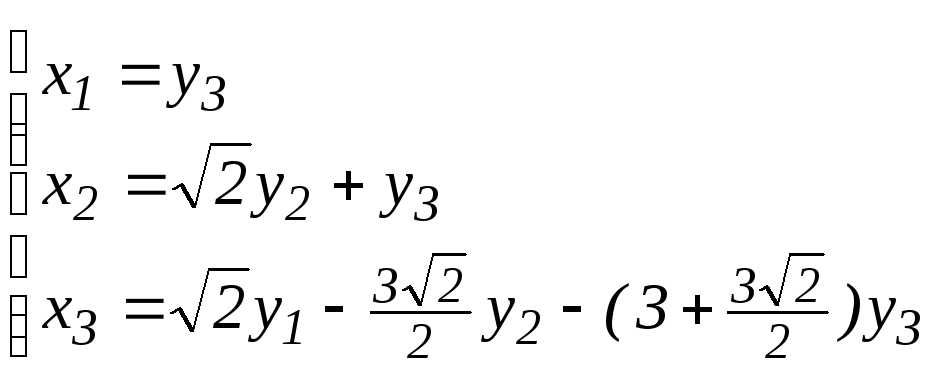 .
.
9.11.
![]() .
9.12.
.
9.12.
![]() .
9.13.
.
9.13.
![]() .
9.14.
.
9.14.
![]() .
.
9.15.
![]() .
9.16.
нет. 9.17.
а) нет; б) да. 9.18.
А(0, 2, 9/5). 10.1.
-1. 10.2.
-4/9. 10.3.
0. 10.4.
-4/5. 10.5.
2/3. 10.6.
-13. 10.7.
45.
10.8.
.
9.16.
нет. 9.17.
а) нет; б) да. 9.18.
А(0, 2, 9/5). 10.1.
-1. 10.2.
-4/9. 10.3.
0. 10.4.
-4/5. 10.5.
2/3. 10.6.
-13. 10.7.
45.
10.8.
![]() .
11.1.
24,5. 11.2.
.
11.1.
24,5. 11.2.
![]() .
11.3.
1)
.
11.3.
1)
![]() ;
2)
;
2)
![]() .
11.4.
1.
11.5.
.
11.4.
1.
11.5.
![]() .
11.6.
.
11.6.
![]() .
11.7.
нет. 11.8.
.
11.7.
нет. 11.8.
![]() .
11.9.
да. 11.10.
-3. 11.11.
54. 11.12.
.
11.9.
да. 11.10.
-3. 11.11.
54. 11.12.
![]() ,
,
![]() .
11.13.
D1(0;-8;0); D2(0;-7;0). 12.1.
-1,5. 12.2.
8x+12y+5=0.
12.3.
2x+3y-7=0.
12.4.
-3x+5y-9=0.
12.5.
A(2,1),
B(4,2),
C(1,8),
D(-1,7).
12.6.
=-4, d=4.
12.7.
.
11.13.
D1(0;-8;0); D2(0;-7;0). 12.1.
-1,5. 12.2.
8x+12y+5=0.
12.3.
2x+3y-7=0.
12.4.
-3x+5y-9=0.
12.5.
A(2,1),
B(4,2),
C(1,8),
D(-1,7).
12.6.
=-4, d=4.
12.7.
![]() .
12.8.
4. 12.9.
по одну. 12.10.
AB:
4x+3y-8=0;
AD: 3x-4y-6=0; BC: 3x-4y+19; CD: 4x+3y-33=0 или
4x+3y+17=0. 12.11.
20x-8y-9=0. 12.12.
x+y-5=0. 12.13.
а)
45
;
б)
60.
12.14.
.
12.8.
4. 12.9.
по одну. 12.10.
AB:
4x+3y-8=0;
AD: 3x-4y-6=0; BC: 3x-4y+19; CD: 4x+3y-33=0 или
4x+3y+17=0. 12.11.
20x-8y-9=0. 12.12.
x+y-5=0. 12.13.
а)
45
;
б)
60.
12.14.
![]() .
12.15.
AB: x-y-7=0;
CD: x+y-5=0; BE: 3x-y-13=0;
CF:
5x+3y-19=0.
13.1.
.
12.15.
AB: x-y-7=0;
CD: x+y-5=0; BE: 3x-y-13=0;
CF:
5x+3y-19=0.
13.1.
![]() .
13.2.
.
13.2.
![]() .
13.3.
.
13.3.
![]() .
.
13.4.
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)![]() .
13.5.
1)
.
13.5.
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5)![]() ;
6)
;
6)
![]() ;
7)
;
7)
![]() ;
8)
;
8)
![]() или
или
![]() ;
9)
;
9)
![]() .
13.6.
.
13.6.
![]() .
13.7.
1)
.
13.7.
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)![]() ;
5)
;
5)
![]() ;
6)
;
6)
![]() .
13.8.
.
13.8.
![]() .
13.9.
.
13.9.
![]() .
13.10.
1) (1,0); 2) (0,2); 3) (-1,0); 4) (0,-1/2). 13.11.
вершина т. О(4,3), фокус т. F(4,
23/8), ось x-4=0,
директриса 8y-25=0.
14.1.
1)
.
13.10.
1) (1,0); 2) (0,2); 3) (-1,0); 4) (0,-1/2). 13.11.
вершина т. О(4,3), фокус т. F(4,
23/8), ось x-4=0,
директриса 8y-25=0.
14.1.
1)
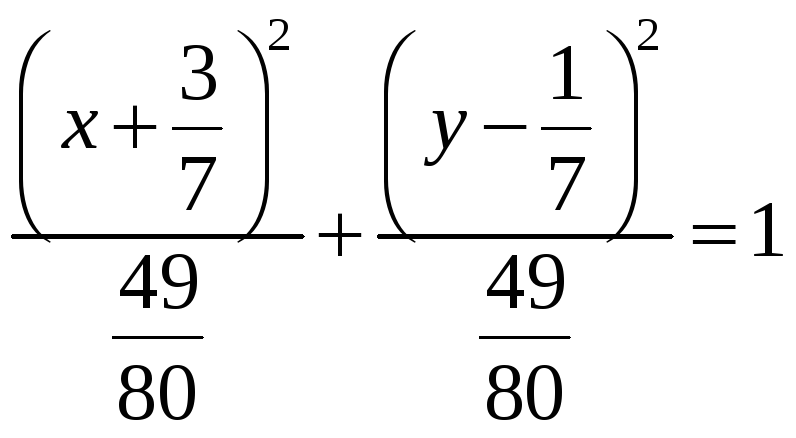 - окружность; 2)
- окружность; 2)
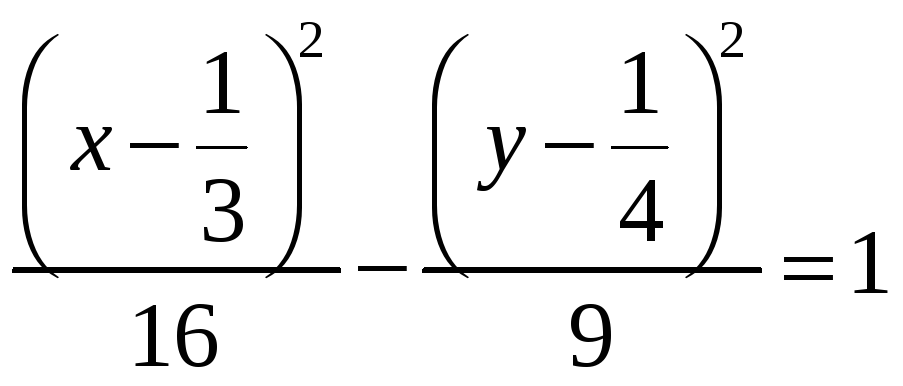 - гипербола; 3)
- гипербола; 3)
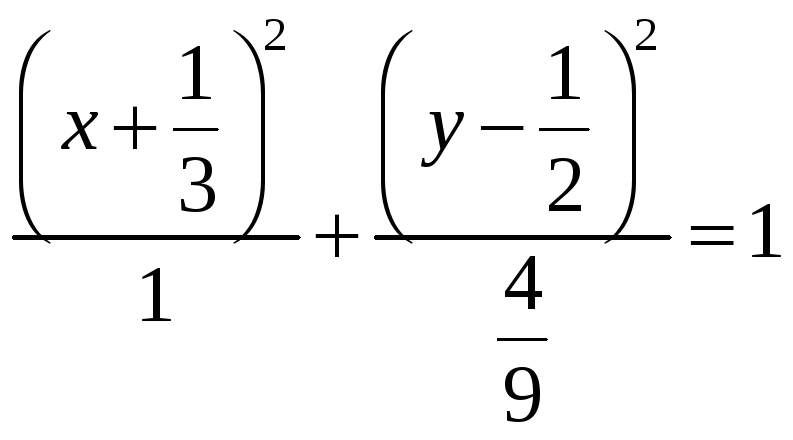 - эллипс; 4)
- эллипс; 4)
![]() - парабола; 5) пара параллельных прямых;
6) мнимый эллипс. 14.2.
1) эллипс; 2) гипербола; 3) парабола; 4) пара
параллельных прямых; 5) пара совпадающих
прямых. 14.3. 1) эллипс; 2) пара пересекающихся
прямых; 3) гипербола; 4) пара параллельных
прямых; 5) гипербола. 14.4.
- парабола; 5) пара параллельных прямых;
6) мнимый эллипс. 14.2.
1) эллипс; 2) гипербола; 3) парабола; 4) пара
параллельных прямых; 5) пара совпадающих
прямых. 14.3. 1) эллипс; 2) пара пересекающихся
прямых; 3) гипербола; 4) пара параллельных
прямых; 5) гипербола. 14.4.
![]() .
14.5.
.
14.5.
![]() .
15.1.
x-2y+3z=0. 15.2.
.
15.1.
x-2y+3z=0. 15.2.
![]() .
15.3.
2x+2y+z=0.
15.4.
10x+3y+16z-78=0.
15.5.
x+y+z-4=0.
15.6.
2x-3y+4z=0.
15.7.
2. 15.8.
x+y-z=4.
15.9.
.
15.3.
2x+2y+z=0.
15.4.
10x+3y+16z-78=0.
15.5.
x+y+z-4=0.
15.6.
2x-3y+4z=0.
15.7.
2. 15.8.
x+y-z=4.
15.9.
![]() .
15.10.
.
15.10.
![]() .
15.11.
4x+3y=0.
15.12.
4. 15.13.
2x-2y-z+12=0;
2x-2y-z-18=0.
16.1.
1)
.
15.11.
4x+3y=0.
15.12.
4. 15.13.
2x-2y-z+12=0;
2x-2y-z-18=0.
16.1.
1)
![]() ,
2)
,
2)
![]() .
16.2.
11/26. 16.3.
.
16.2.
11/26. 16.3.
![]() .
16.4.
.
16.4.
![]() .
16.5.
.
16.5.
![]() ;
;
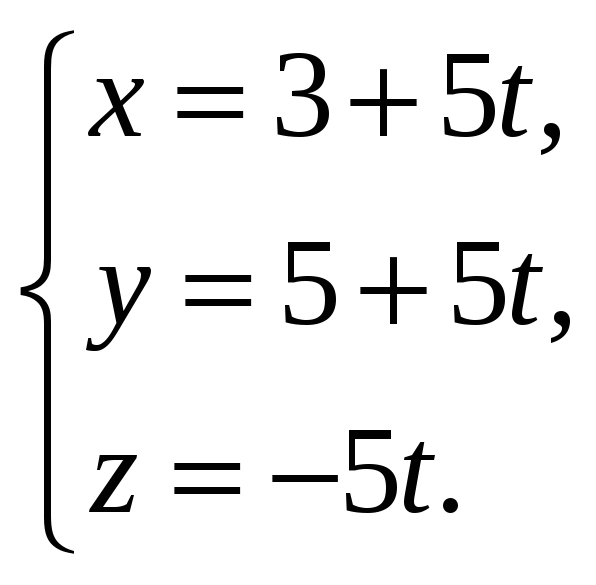 .
16.6.
.
16.6.
![]() .
16.7.
.
16.7.
![]() .
17.1.
(1,2,3). 17.2.
(48/19, -53/19, 70/19).
17.3.
(-31/14; 27/14; 20/14). 17.4.
(197/75, 46/75, 10/ 75) . 17.5.
(1,4,-7). 17.6.
(A(4,1,-3)).
17.7.
(0,-3,-2).
17.8.
10x-21y+8z+3=0. 17.9.
13x-14y+11z+51=0. 17.10.
6x-4y+z=0.
17.11.
-2x+16y+13z-31=0.
17.12.
.
17.1.
(1,2,3). 17.2.
(48/19, -53/19, 70/19).
17.3.
(-31/14; 27/14; 20/14). 17.4.
(197/75, 46/75, 10/ 75) . 17.5.
(1,4,-7). 17.6.
(A(4,1,-3)).
17.7.
(0,-3,-2).
17.8.
10x-21y+8z+3=0. 17.9.
13x-14y+11z+51=0. 17.10.
6x-4y+z=0.
17.11.
-2x+16y+13z-31=0.
17.12.
![]() .
17.13.
.
17.13.
![]() .
17.14.
d=3,
2x+y+2z-8=0.
18.1.
1) при
.
17.14.
d=3,
2x+y+2z-8=0.
18.1.
1) при
![]() эллипсоид, при
эллипсоид, при
![]() пустое
множество; 2) при
пустое
множество; 2) при
![]() эллипсоид, при
эллипсоид, при
![]() однополостной
гиперболоид, при
однополостной
гиперболоид, при
![]() эллиптический цилиндр; 3) при
эллиптический цилиндр; 3) при
![]() двуполостной гиперболоид, при
двуполостной гиперболоид, при
![]() однополостной
гиперболоид, при
однополостной
гиперболоид, при
![]() конус; 4) при
конус; 4) при
![]() эллиптический параболоид; при
эллиптический параболоид; при
![]() прямая; 5) при
прямая; 5) при
![]() гиперболический цилиндр; при
гиперболический цилиндр; при
![]() пара пересекающихся плоскостей.
18.2.
пара пересекающихся плоскостей.
18.2.
![]() .
18.3.
1) А(2,2,2), R=2
.
18.3.
1) А(2,2,2), R=2![]() ;
2) А(-1,-2-3), R=
;
2) А(-1,-2-3), R=![]() .
18.4.
1) эллипсоид: центр О(-1,-1,-1), полуоси
.
18.4.
1) эллипсоид: центр О(-1,-1,-1), полуоси
![]() ,
,![]() ,
,![]() ,
плоскости симметрии
,
плоскости симметрии
![]() ;
2) двуполостной гиперболоид: центр
О(-3,1,1), вершины А(-5,1,1),
;
2) двуполостной гиперболоид: центр
О(-3,1,1), вершины А(-5,1,1),
В(-1,1,1),
ось симметрии
![]() ,
плоскости симметрии
,
плоскости симметрии
![]() .
18.5.
1) параболический цилиндр; 2) эллиптический
параболоид; 3) эллиптический параболоид;
4) однополостной гиперболоид; 5) конус;
6) двуполостной гиперболоид; 7)
гиперболический параболоид; 8) эллиптический
цилиндр. 18.6.
1) эллипсоид; 2) конус; 3) параболический
цилиндр; 4) эллиптический параболоид,
5) однополостной гиперболоид.
.
18.5.
1) параболический цилиндр; 2) эллиптический
параболоид; 3) эллиптический параболоид;
4) однополостной гиперболоид; 5) конус;
6) двуполостной гиперболоид; 7)
гиперболический параболоид; 8) эллиптический
цилиндр. 18.6.
1) эллипсоид; 2) конус; 3) параболический
цилиндр; 4) эллиптический параболоид,
5) однополостной гиперболоид.
