4. Уравнение плоскости по трем точкам

В векторном виде

В координатах

или

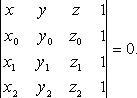
5. Уравнение плоскости в векторной форме

 где

- радиус- вектор текущей точки М(х, у, z),

 - единичный вектор, имеющий направление, перпендикуляра, опущенного на плоскость из начала координат.

,  и  - углы, образованные этим вектором с осями х, у, z.

p – длина этого перпендикуляра.

В координатах это уравнение имеет вид:

xcos + ycos + zcos - p = 0

6. Частные случаи общего уравнения плоскости:

1) By + Cz + D = 0 - параллельна оси Ox;

2) Ax + Cz + D = 0 - параллельна оси Oy;

3) Ax + By + D = 0 - параллельна оси Oz;

4) Cz + D = 0 - параллельна оси Oxy;

5) By + D = 0 - параллельна оси Oxz;

6) Ax + D = 0 - параллельна оси Oyz;

7) Ax + By + Cz = 0 - проходит через начало координат;

8) By + Cz = 0 - проходит через ось Ox;

9) Ax + Cz = 0 - проходит через ось Oy;

10) Ax + By = 0 - проходит через ось Oz;

11) z = 0 - плоскость Oxy;

12) y = 0 - плоскость Oxz;

13) x = 0 - плоскость Oyz.

7.    Угол между плоскостями 

8. Условие параллельности плоскостей  Ах+ Ву+ Сz+ D = 0  и  Eх+ Fу+ Gz+ H = 0:

AF – BE = BG – CF = AG – CE = 0 .

9.Условие перпендикулярности плоскостей  Ах+ Ву+ Сz+ D = 0  и  Eх+ Fу+ Gz+ H = 0:

АE+ ВF+ СG = 0 .

10. Расстояние от точки  ( х₀ ,  у ₀ ,  z ₀ )  до плоскости  Ах + Ву + Сz + D = 0 :

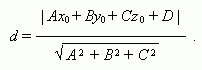
Прямая в пространстве.

1. Каноническое уравнение прямой 

2. Уравнение прямой, проходящей через две точки: A(x₁, y₁) и B(x₂, y₂), записывается так:

3.  Угол между двумя прямыми 

     4. Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

     (10)

Это условие может быть записано также в виде

k₁k₂ = -1.     (11)

б) Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства

A₁A₂ + B₁B₂ = 0.     (12)

5.

Условия параллельности двух прямых:

а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k₁ = k₂.     (8)

б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

     (9)

6. Угол между прямой и плоскостью

Если прямая параллельна плоскости, то Am+Bn+Cp=0

Если прямая перпендикулярна плоскости, то

7. Условие параллельности прямой и плоскости

Аl + Вm + Сn = 0

8.

Определение 3.3.

Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой из этой плоскости.

Теорема 3.1. Признак перпендикулярности прямой и плоскости.

Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости.

Доказательство

Сформулируем некоторые теоремы, устанавливающие связь между параллельностью и перпендикулярностью в пространстве.

Теорема 3.2.

Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой.

Чертеж 3.2.2.

Теорема 3.3.

Две прямые, перпендикулярные одной плоскости, параллельны между собой.

Теорема 3.4.

Если прямая перпендикулярна одной из двух параллельных плоскостей, то она перпендикулярна и другой.

Теорема 3.5.

Две плоскости, перпендикулярные одной прямой, параллельны между собой.

9.

Точка пересечения прямой с плоскостью 

В координатах:

где