2.3.2. Виды зубчатых колес

При проектировании зубчатой передачи возникает вопрос о выборе коэффициентов смещения, которые определяют положение делительной прямой зубчатой инструментальной рейки (режущего инструмента) относительно делительной окружности нарезаемого колеса.

В реечном зацеплении делительная прямая рейки может располагаться различным образом по отношению к делительной окружности колеса. В зависимости от сдвига рейки зубчатые колеса бывают:

• Нулевые.

• Положительные.

• Отрицательные.

Е

сли нет смещения (а = 0), то такое колесо называется нулевым.

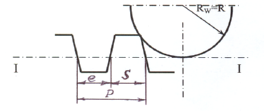
Толщина зуба S равна ширине впадины е и равна половине шага:

S = e, S =p.

• Если смещение а направлено в сторону от оси нарезаемого колеса, то колесо называется положительным.

Толщина зуба S больше, чем ширина впадины е: S > e, S >p.

• Если смещение a рейки направлено в сторону оси нарезаемого колеса, это колесо называется отрицательным.

Толщина зуба S меньше, чем ширина впадины е

S < e, S < p.

2.3.3. Виды зацепления зубчатых передач в зависимости от смещения рейки

В зависимости от величин смещения каждого колеса можно получить три вида зацепления передач, отличающихся расположением начальных и делительных окружностей.

а). Нулевое зацепление. Данная передача составлена из нулевых колес. Начальные и делительные окружности совпадают, действительный угол зацепления равен стандартному (α_w = α= 20^o).

б). Равносмещенное зацепление. Эта передача составлена из положительного и отрицательного колеса с одинаковыми по абсолютной величине коэффициентами смещения. Начальные и делительные окружности совпадают и угол зацепления равен 20^о. Отличие от нулевого зацепления заключается в том, что толщина зуба шестерни увеличивается, а у второго колеса - уменьшается, поэтому шаг остается таким же, как и при нулевой передаче (S₁ = e₂; S₂ = e₁, где е – ширина впадины).

в). Неравносмещенное зацепление. Эта передача может быть составлена из положительного и нулевого колеса или из двух положительных колес. Делительные окружности не совпадают с начальными и действительный угол зацепления больше стандартного (α_w > 20^о). Сумма толщин зубьев не равна шагу (S₁ + S₂ > P). Поэтому, чтобы вписать данную передачу в заданный шаг, применяют коэффициент уравнительного смещения Δу.

2.3.4. Определение размеров зубчатой передачи

Размеры колес, а так же всего зацепления, зависят от чисел зубьев колес Z₁ и Z₂, от модуля m зацепления, общего для обоих колес, а также от метода их обработки.

Формулы для определения размеров элементов цилиндрического зацепления с прямым зубом представлены в табл. 1 приложения.

На основании известных Z₁, Z₂, и U₁₂ определим коэффициенты смещения Х₁, Х₂, для равносмещенного зацепления по таблице приложения 6, а для неравносмещенного зацепления коэффициенты Х₁, Х₂ и Δу в зависимости от передаточного отношения:

а) если 2≥ U₁₂ ≥1, то Х₁, Х₂ определяются по таблице приложения 4, Δу - по таблице 2.

б) если 2≤U₁₁≤5, то Х₁ и Δу по таблице 3, Х₂ - по таблице 5.

2.3.5. Геометрические элементы зубчатых колес

Радиусы начальных окружностей R_W – радиусы окружностей колес, соприкасаемых в точке полюса р, перекатываемых без скольжения. Поэтому, межосевое расстояние а_W можно вычислить по формуле

а_W=[O₁O₂] = R_W1+ R_W2. (11)

Радиус делительной окружности R – радиус, который делит высоту зуба на ножку и головку (рис. 3).

Для нулевой (стандартной) передачи радиус делительной окружности равен радиусу начальной, т.е.

R = R_W.

Модуль зубчатого зацепления m – отношение шага Р к числу π:

. (12)

Модуль – это стандартная величина, выбираемая их ряда рациональных чисел согласно ГОСТ 9563-60; измеряется в мм.

В первом, предпочтительном ряду предусмотрены следующие модули в мм: 0,05; 0,06; 0,08; 0,1; 0,12; 0,15; 0,2; 0,25; 0,3; 0,4; 0,5; 0,6; 0,8; 1,0; 1,25; 1,5; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25; 32; 40; 50; 60; 80; 100. Во втором ряду предусмотрены модули, промежуточные между модулями первого ряда, например: 3,5; 4,5; 5,5; 7; 9; 11 и др.

Шаг зубчатого зацепления Р – расстояние по делительной окружности между одноименными точками двух соседних зубьев.

Высота зуба h – расстояние между окружностями впадин R_f и выступов R_a. Высота зуба складывается из высоты ножки зуба h_f и высоты головки зуба h_а

h= h_f + h_а. (13)

Для нулевого (стандартного) колеса h_a =m, h_f = 1,25m, тогда

h=2,25m.

Радиус основной окружности R_b – радиус, с которого начинается построение эвольвенты.

Эвольвента – развертка круга, боковая поверхность зуба.

Радиус окружности впадин R_f – радиус, ограничивающий ножку (впадину) зуба.

Радиус окружности выступов R_а – радиус, ограничивающий головку (вершину) зуба.