7.4.1. Разностная схема уравнений

Разностную схему рассмотрим на примере уравнения Пуассона в прямоугольнике, используя для аппроксимации второй производной конечные разности второго порядка точности (7.1.4). Вводя сетку , получаем ,

или , введя обозначение , получаем пятиточечную разностную схему для внутренних узлов прямоугольника

(7.4.1)

Данная неявная схема охватывает все внутренние точки области , их количество . Таково же число уравнений и неизвестных в СЛАУ, построенной на основе (7.4.1).

Пусть для простоты для всех , т.е. для всех внутренних точек , , а граничные условия таковы: внизу , слева и справа , и только наверху задана отличная от нуля функция . Зададим , . Тогда , а число внутренних точек и уравнений . Матрица СЛАУ для данной задачи задается по следующему закону (на языке пакета Mathcad):

Здесь , - это индексы матрицы , они связаны с другими, ранее введенными индексами для узлов сетки. Сеточная функция , , выражается через найденный в результате решения СЛАУ вектор решения , следующим образом: .

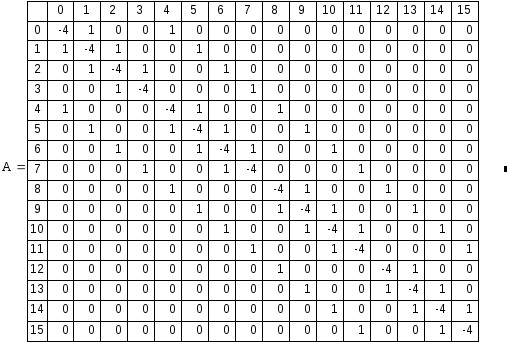
Пятидиагональная матрица имеет следующее строение:

Вектор правой части СЛАУ задается в данной задаче по закону:

,

где - число, определяющее в индексах вектора решения начало последнего слоя внутренних узлов по оси , на которых учитывается заданное граничное условие. Заданная функция из уравнения, в данной задаче являющаяся константой, , входит в правую часть СЛАУ в виде слагаемого . Значения вектора правой части в данной задаче:

На рис.3 показано распределение функции решения аналогичной краевой задачи в двумерной области при порядке СЛАУ . Решение получено комбинированным методом Зейделя-ОСП при оптимальном параметре за итераций с относительной точностью решения в . Обычный метод Зейделя сходится здесь лишь за итераций и сопоставим по времени решения с прямым методом. Еще большее число требуемых итераций показывают в данной задаче метод ОСП с матрицей (1.2) - .

Отметим, что матрица задачи при и заданном постоянна и не зависит от краевых условий и источников , которые входят в правую часть СЛАУ. Соответственно задачи с различными краевыми условиями и источниками могут решаться с тем же самым оптимальным параметром, найденным один раз для данной сетки.

рис.3

5. Лабораторные задания к теме «Численное решение уравнений в частных производных»

Лабораторные работы по теме могут быть выполнены с помощью математических пакетов программ Mathcad или Matlab. В результате работы должна быть представлена искомая сеточная функция в виде матрицы значений в узлах сетки либо в виде послойного по времени распределения значений сеточных векторов. Следует также привести графическое представление результатов.

7.5.1. Гиперболические уравнения

Варианты заданий для одномерного волнового уравнения с граничными и начальными условиями (см. 7.2).

№ п/п									Метод
1.1	1	1	0	0			2	0.1, 0.05	1
1.2	1	2	0	0			1	0.1, 0.05	1
1.3		1	0	0			2	0.1, 0.05	1
1.4	1	2	0	0			1	0.1, 0.05	1
1.5		1	0	0			2	0.1, 0.05	1
1.6	1	2	0	0			1	0.1, 0.05	1
1.7		1	0	0			2	0.1, 0.05	1
1.8	1	2	0	0			1	0.1, 0.05	1
1.9		1	0	0			2	0.1, 0.05	1
1.10	1	2	0	0			1	0.1, 0.05	1