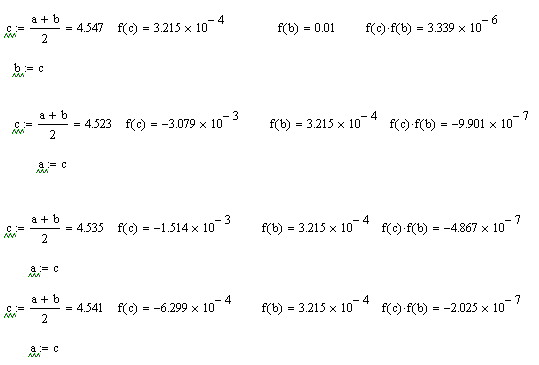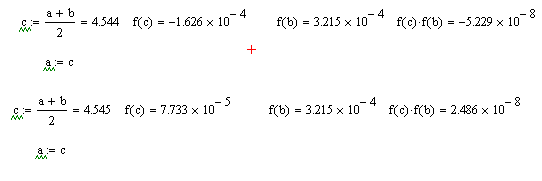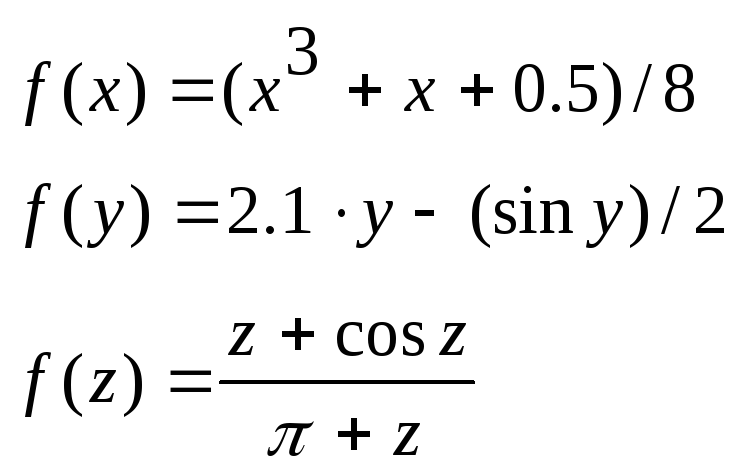МІНІСТЕРСТВО ОСВІТИ, НАУКИ молоді та спорту УКРАЇНИ

ЧЕРКАСЬКИЙ ДЕРЖАВНИЙ ТЕХНОЛОГІЧНИЙ УНІВЕРСИТЕТ

Кафедра інформатики та інформаційної безпеки

Контрольна робота

по курсу “Інформаційні системи та технології”

на тему: “Реалізація чисельних методів в Mathcad”

Керівник Пригодюк О. М. Виконав:

Роботу допущено до захисту студент IV курсу ФЕТ

“___” _____________ 2011 р. гр.СКЗЕСЕ-108

Роботу захищено з оцінкою Кандауров к. В.

________________________

“___” _____________ 2011 р.

Черкаси 2011 р.

Завдання 1 Табулювання складної функції

Звіт по роботі повинен включати:

1. Теоретичну частину.

2. Постановку задачі.

3.Протабулювати функцію свого варіанту та представити її графіком в MathCad

1. РіШення неЛіНіЙних рівнянь

Метод половинного ділення (дихотомії)

Це найпростіший метод уточнення коренів. Його сутність полягає в наступному.

Відрізок ізоляції кореня рівняння ділимо навпіл і в серединній точці с знаходимо значення функції . Далі в точку с переносимо одну із точок a або b, в якій знак функції співпадає зі знаком функції в точці с. Таким чином, корінь рівняння залишається в двічі звуженому діапазоні . Тобто,

1. якщо то відбувається заміна точок ;

2. або якщо то відбувається заміна точок

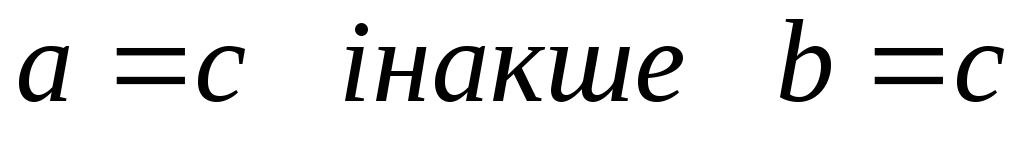
Процес ділення продовжуємо до тих пір, поки значення функції в точці с з заданою точністю не стане близьким до нуля, тобто Хід ітераційного процесу представлений на рисунку 1. Через n ітерацій інтервал буде звужений в разів.

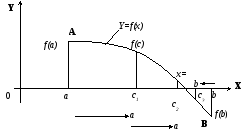
2.Завдання

0

5

0,25

3.

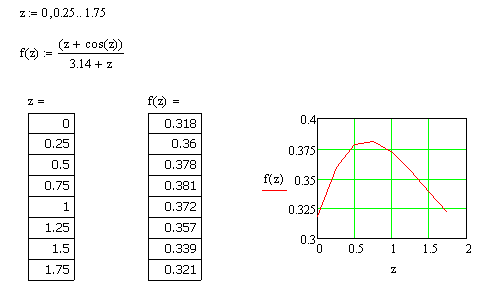
Завдання 2

Розв’язок нелінійного рівняння

1. Теоретичну частину.

2. Постановку задачі.

3. Графічне відокремлення кореня, уточнення за допомогою X-Y Trace.

4. Уточнення кореня з використанням функції root.

5. Обчислення нелінійного рівняння за допомогою вбудованих функцій:

обчислити корені рівняння за допомогою вбудованої функції Find враховуючи періодичність функції;

6.Уточнення кореня в MathCad методом половинного ділення (дихотомії)

1. Уточнення коренів методом хорд

Нехай задане рівняння , де - безперервна функція, яка має в інтервалі [a, b] похідні першого та другого порядків.

Корінь відділений, знаходиться на відрізку [a ,b], тобто <0. Ідея метода полягає в тому, що на достатньо малому відрізку [a, b] дуга кривої замінюється стягуючою її хордою. Як наближене значення кореня приймається точка перетину хорди з віссю Ох (мал. 2).

Мал. 2. Метод хорд.

Розглянемо випадки , коли перша та друга похідні мають однакові знаки, тобто >0.

Нехай <0, >0, >0 та >0 (мал. 2, а). Графік функції проходить через точки та . Корінь рівняння є абсциса точки перетину графіка функції з віссю Ох. Ця точка поки невідома. Якщо ми замінимо дугу А₀В хордою А₀В , то точка перетину хорди з віссю Ох х₁ буде приближеним значенням кореня.

Рівняння хорди , яка проходить через точки А₀ та В має вид:

Знайдемо значення , для якого

(1)

Ця формула називається формулою хорд.

Тепер корінь рівняння знаходиться в середині відрізка [x₁, b]. Якщо значення кореня нас не задовольняє , його можна уточнити, примінюючи метод хорд для відрізка [x₁, b].

З’єднаємо точки з точкою і знайдемо точку перетину хорди з віссю Ох.

Продовжити процес , знаходимо

взагалі

(2)

Процес продовжуємо до тих пір , поки поки не визначимо корінь із заданою точністю, тобто , де - задана точність.

По вище приведеним формулам обчислюються корені для випадку, коли (мал. 2, б).

2.Постановка задачі.

3. Графічне відокремлення кореня, уточнення за допомогою X-Y Trace

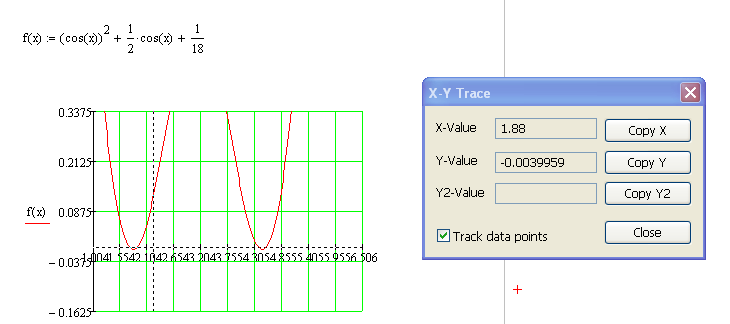
4.Уточнення кореня з використанням функції root.

5. Обчислення нелінійного рівняння за допомогою вбудованих функцій:

Find

6.Уточнення кореня в MathCad:методом половинного ділення