8.3. Производство в долгосрочный период.
В долгосрочный период все факторы производства могут быть переменными. Поэтому один и тот же объем выпуска продукции - Q может быть обеспечен путем использования различных комбинаций переменных факторов. (X1, X2,...Xn)
Q=f(X1,X2,...Xn),
Постоянная Переменные
величина величины
Перед каждым производителем в долгосрочный период стоит проблема выбора: как именно произвести ту или иную продукцию? Какие ресурсы использовать в большей или меньшей степени? Ответ на поставленные вопросы зависит не только от характера технологии, но и от стоимости ресурсов, следовательно, проблема выбора решается с позиций технологической и экономической эффективности.
Для точного определения условий эффективного производства данного объема выпуска продукции используем графический метод анализа производственной функции через изокванты( оценивают уровни технологической эффективности) и изокосты(оценивают уровни экономической эффективности).
8.3.1. Изокванты.
Для простоты анализа, как и прежде, будем полагать, что
· исследуемая функция производства зависит от двух факторов: труда и капитала,
· является частным случаем функции Кобба-Дугласа и имеет вид
Q=KL;
· факторы производства в определенных пределах являются взаимозаменяемыми;
· технология производства в течение всего рассматриваемого периода не меняется.
Представим в виде таблицы данную функцию для значений K и L от 1 до 4.
Таблица 2. Производственная функция
|
L K |
1 |
2 |
3 |
4 |
|
1 |
1 |
2 |
3 |
4 |
|
2 |
2 |
4 |
6 |
8 |
|
3 |
3 |
6 |
9 |
12 |
|
4 |
4 |
8 |
12 |
16 |
Как видно из представленной таблицы, существует несколько комбинаций труда и капитала, обеспечивающих в определенных пределах заданный объем выпуска. Например, Q=4 можно получить, используя комбинации (1,4), (4,1) и (2,2). Аналогичным образом Q=6 можно получить, используя комбинации (2,3) и (3,2) и т.д.
Если отложить по горизонтальной оси количество единиц труда, по вертикальной - количество единиц капитала, затем, обозначить точки, в которых фирма выпускает один и тот же объем, то получится кривая, представленная на рисунке и называемая изоквантой (IQ).
Изокванта (isoquant – от слов “iso”- тот же самый и “quant” –количество) - кривая, каждая точка которой показывает альтернативные комбинации ресурсов, которые могут быть использованы для производства определенного объема продукции при данной технологии.
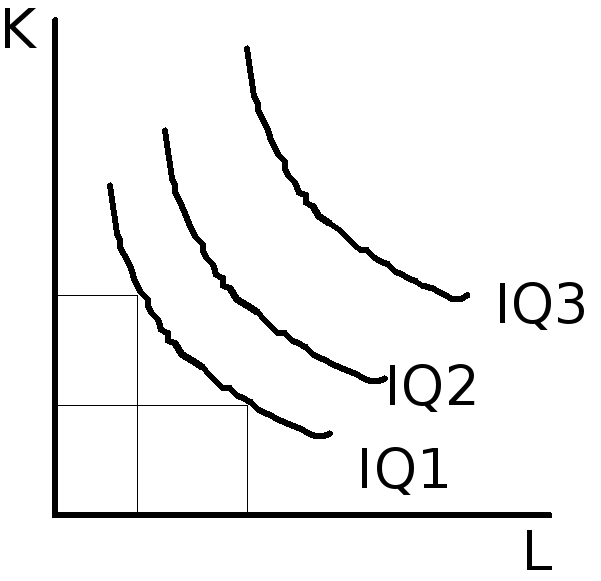
Рис.2. Карта изоквант.
Набор изоквант, характеризующий данную производственную функцию, называется картой изоквант.
Свойства стандартных изоквант аналогичны характеристикам кривых безразличия.
1. Изокванта, также как и кривая безразличия, является непрерывной функцией, а не набором дискретных точек;
2. Для любого заданного объема выпуска может быть проведена своя изокванта, отражающая различные комбинации экономических ресурсов, обеспечивающих производителю одинаковый объем производства.
3. Изокванты, описывающие данную производственную функцию, никогда не пересекаются.
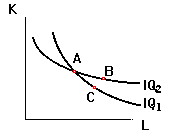
Рис. 3. Изокванты не пересекаются
Пересечение изоквант противоречило бы условию эффективности производства. Для доказательства этого, предположим, что две изокванты для разных объемов имеют одну общую точку А. Отметим на графике еще две произвольные точки В и С, как это изображено на рисунке 3.
Комбинация ресурсов В является более предпочтительной для фирмы, чем комбинация С, поскольку содержит большее количество обоих ресурсов, и следовательно, в соответствии с данной производственной функцией, обеспечивает больший объем выпуска. Вместе с тем комбинации А и В принадлежат одной изокванте, и значит обеспечивают одинаковый объем производства. Комбинации А и С также принадлежат одной изокванте и также обеспечивают одинаковый объем. В соответствии с принципом транзитивности, если А=В и А=С, то и В=С, а это противоречит исходному положению.
4. Изокванты не имеют участков возрастания.
Если бы участок возрастания существовал, то при движении вдоль него увеличивалось бы количество как первого (К), так и второго (L) ресурса, т.е. возростал бы объем максимального выпуска, а он(объем) должен быть постоянным на всем протяжении изокванты.
Убывающий характер изокванты отражает возможность замещения в определенных пределах используемых ресурсов, так что совокупный объем выпуска остается неизменным.