
- •Оглавление
- •Введение
- •Решение некоторых типовых задач
- •3. Тождественные преобразования тригонометрических выражений
- •Ответ: 5 см. Варианты индивидуальных заданий
- •Задание 18
- •Основанием пирамиды служит ромб со стороной а и острым углом . В пирамиду вписан конус, образующая которого наклонена к плоскости основания под углом . Найти объем конуса.
- •Библиографический список
- •Математика
- •660075, Г. Красноярск, ул. Д. Прушинской, 2
3. Тождественные преобразования тригонометрических выражений
Пример 1.
Доказать тождество
![]()
Решение.
Используем формулу
![]()
![]() ,
где
,
где
![]() ,
,
![]() ,
получим
,
получим
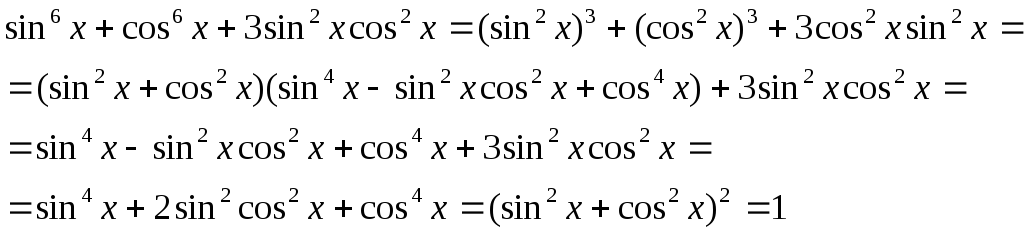
![]()
Тождество доказано.
Пример 2. Упростить выражение
Решение.
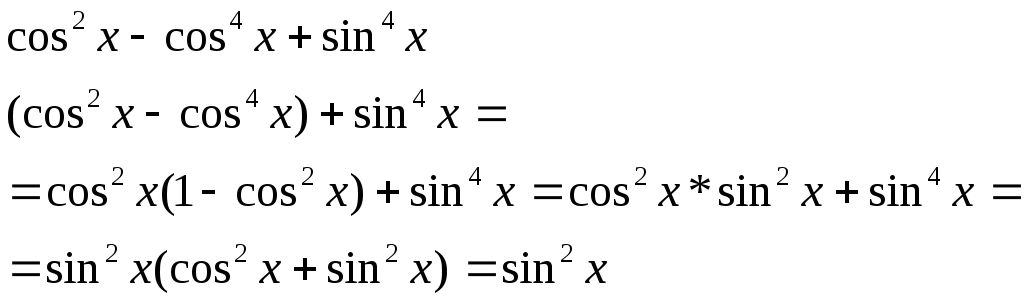
Использовалось
основное тригонометрическое тождество
![]() .
.
Пример 3.
Решить уравнение![]() .
.
При решении тригонометрических уравнений не забудьте обратить внимание на область определения и отбор корней, которые входят в эту область.
Решение.
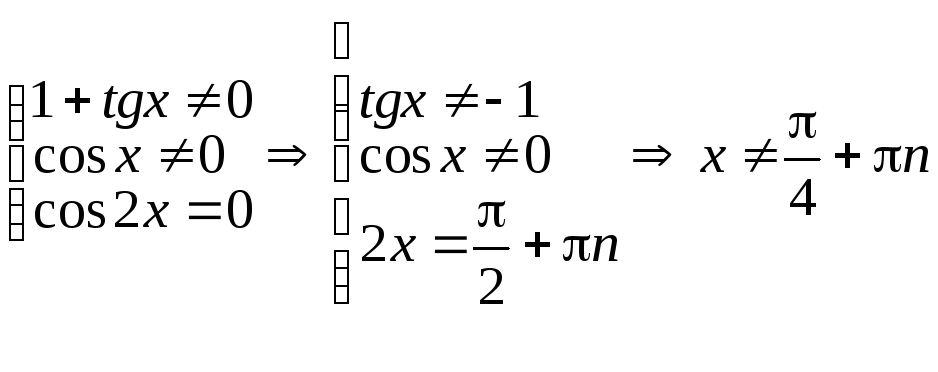 .
.
При нечетном
n(n=2k-1)
получается значения не удовлетворяющие
ОДЗ. Поэтому корнями уравнения будут
значения при четном n(n=2k),
т. е.![]()
Ответ:
![]() .
.
4. Решить задачу
Задача 1. Первое из неизвестных чисел составляет 140 % второго, а отношение первого к третьему равно 14/11. Найти эти числа, если разность между третьим и вторым на 40 единиц меньше числа, составляющего 12,5 % суммы первого и второго чисел.
Решение:
Пусть второе число
х,
тогда первое число -1,4х;
третье –
![]() .
.
Составляем уравнение 1,1x – x = 0,125(1,4x + x) – 40.
Решая уравнение, получим x = 200; 1,4x = 280, 1,1x = 220.
Ответ: 280; 200; 220.
Задача 2. Найти длину основания равнобедренного треугольника, площадь которого равна 25 см2, а углы при основании таковы, что tg = 4.
Дано: ΔАВС равнобедренный;
 SΔАВС
= 25 см2;
tgα
= 4.
SΔАВС
= 25 см2;
tgα
= 4.
Найти: АС
Решение
В треугольнике АВС ВДАС, АВ = ВС. По свойству равнобедренного треугольника АД = ДС. Обозначим ВД = h, АД = а, тогда tg= h/a и SАВС=1\2h 2a= a h.
Получили
систему уравнений
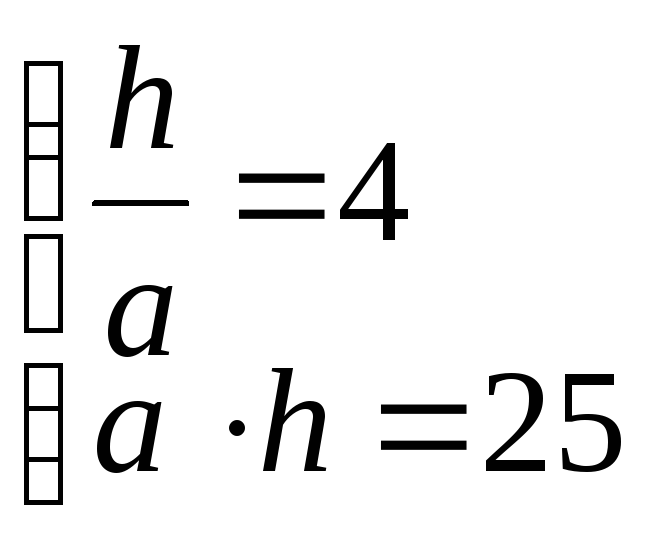 ,
,
h = 4a; 4a2 = 25, a = 2,5 или а = -2,5 (не подходит)
Следовательно, АС = 2а = 5.
Ответ: 5 см. Варианты индивидуальных заданий
Задание 1. Выполнить указанные действия
1.
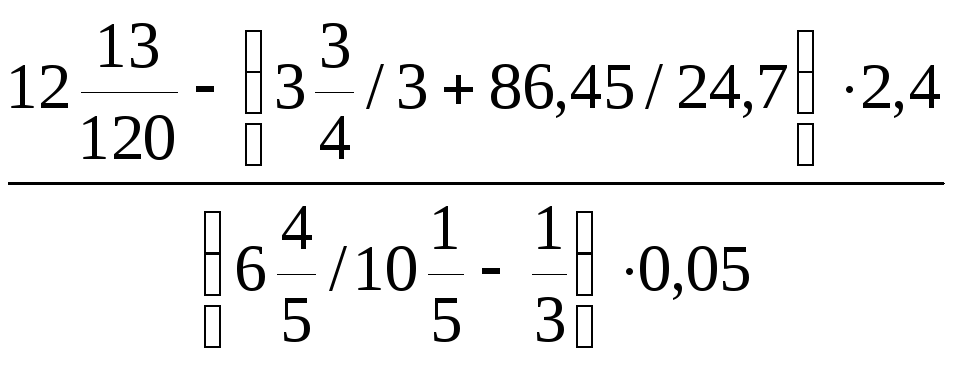 .
.
2.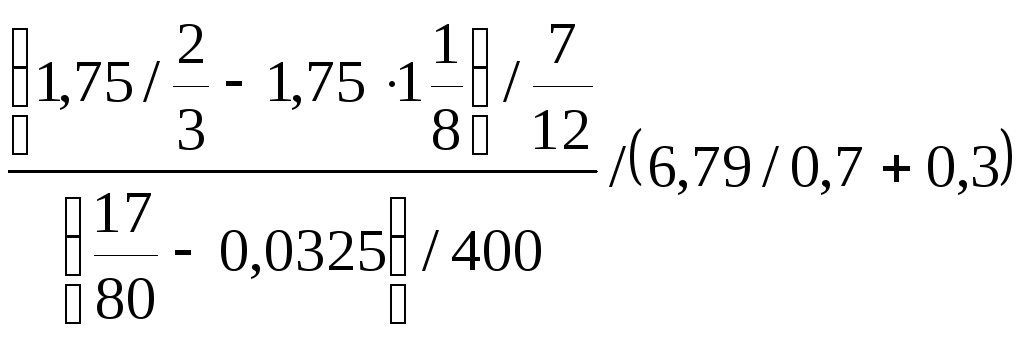 .
.
3. .
.
4.![]() .
.
5.![]() .
.
6.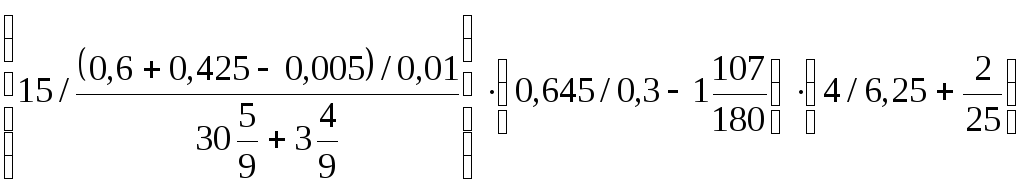 .
.
7. .
.
8.![]() .
.
9.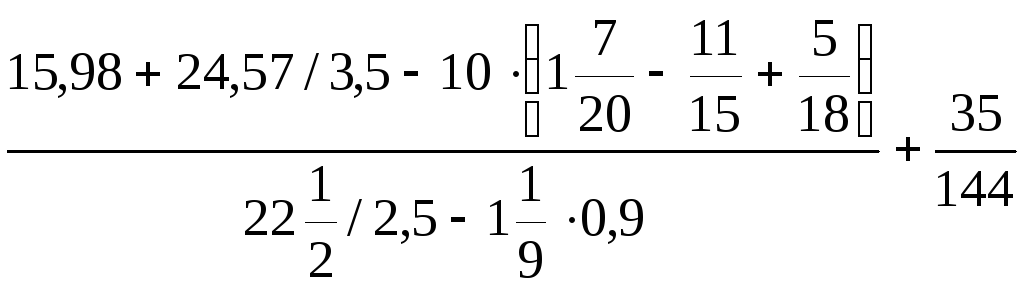 .
.
10.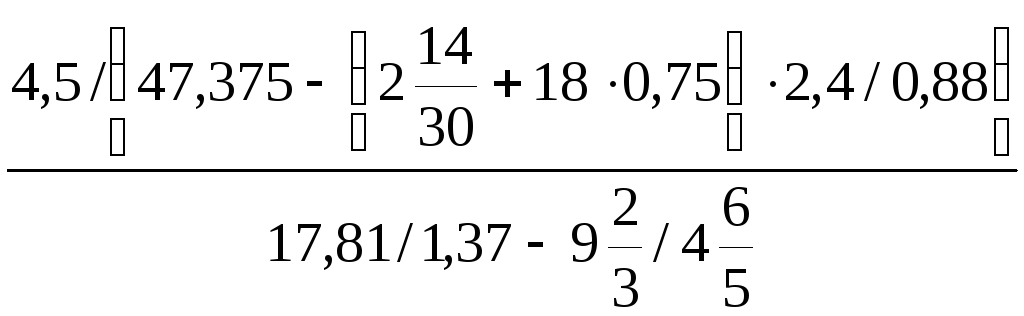 .
.
11.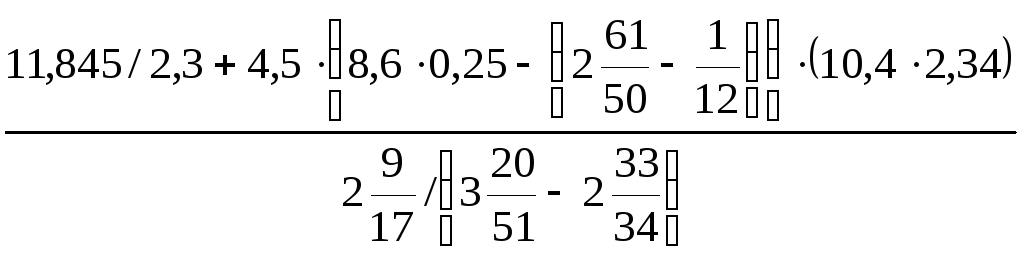 .
.
12.
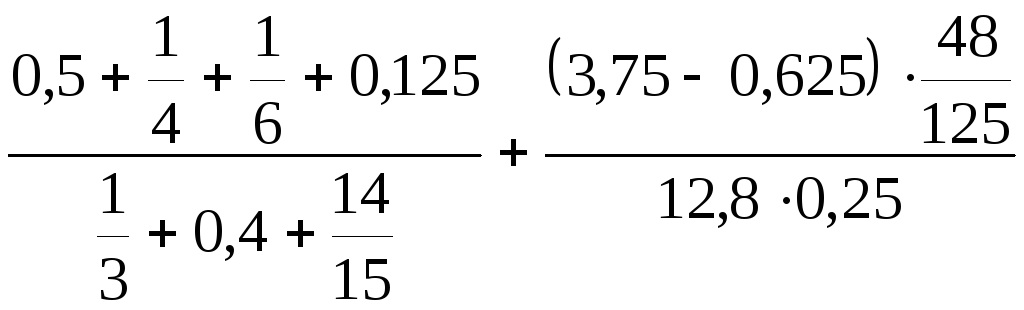 .
.
13.
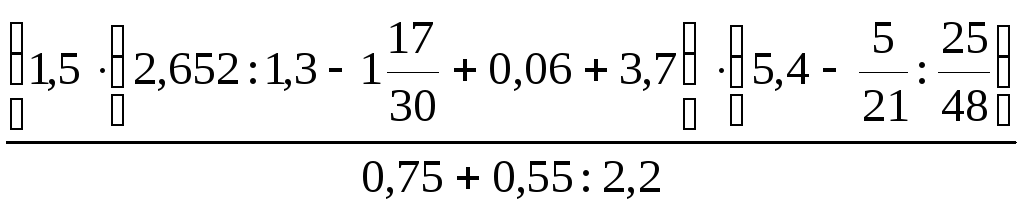 .
.
14.
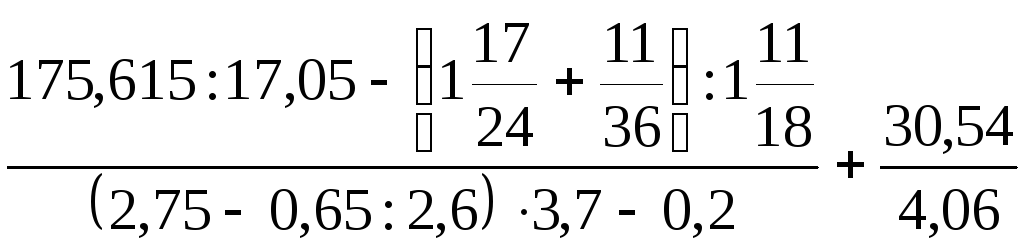 .
.
15.
 .
.
16.
 .
.
17.
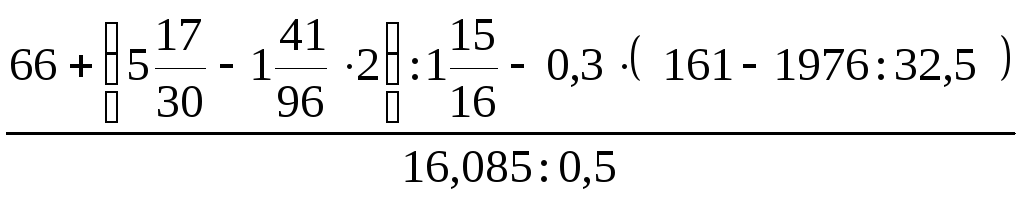 .
.
18.
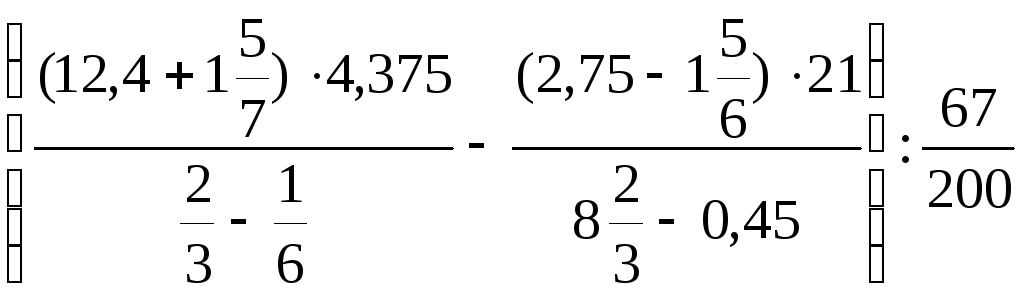 .
.
19.
 .
.
20.
![]() .
.
21.
![]() .
.
22.
![]() .
.
23.
![]() .
.
24.
![]() .
.
25.
![]() .
.
Задание 2. Выполнить указанные действия
1.
![]() .
.
2.
![]() .
.
3.
![]()
4.
 .
.
5.
 .
.
6.
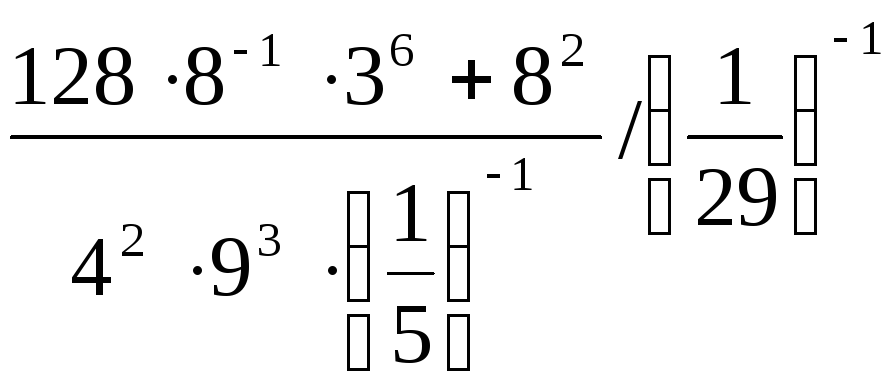 .
.
7.
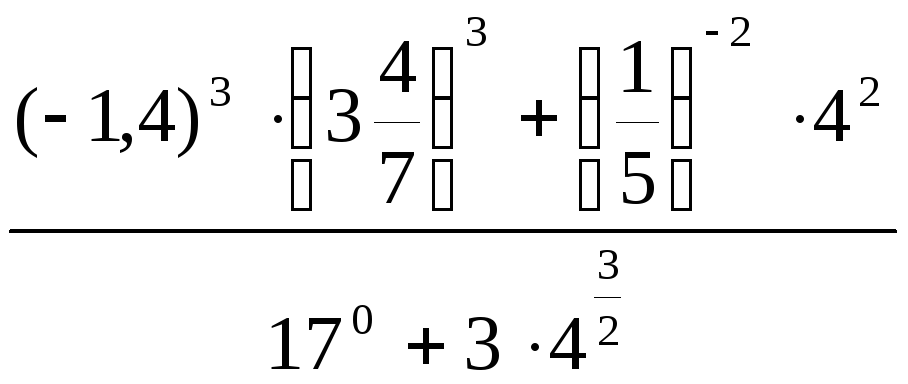 .
.
8.
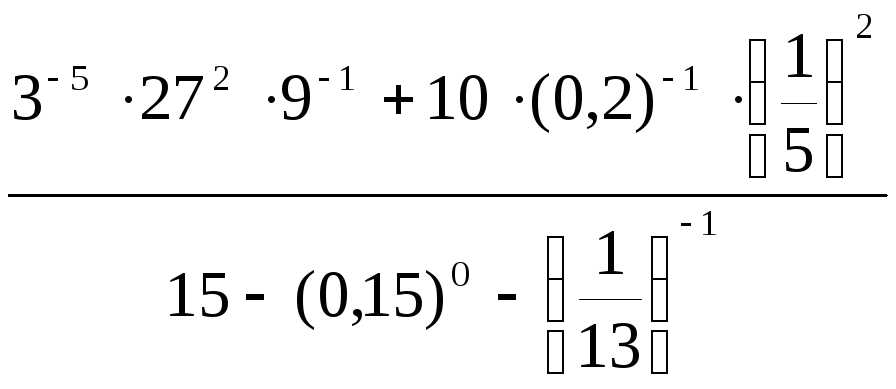 .
.
9.
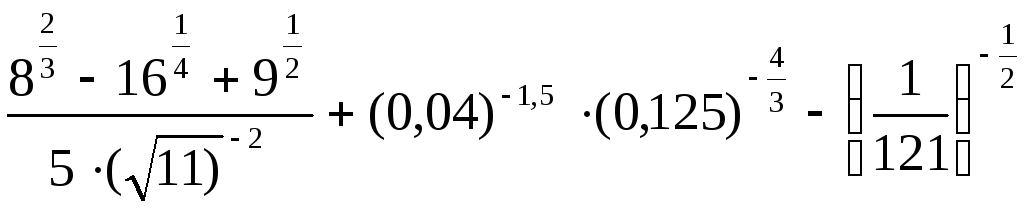 .
.
10.
 .
.
11.
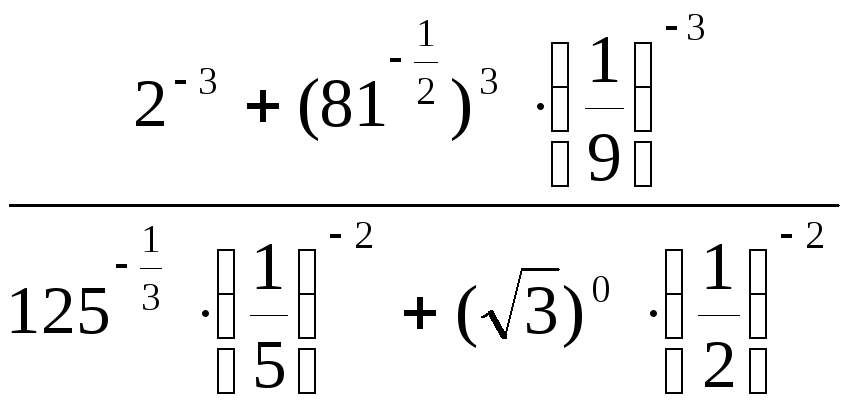 .
.
12.
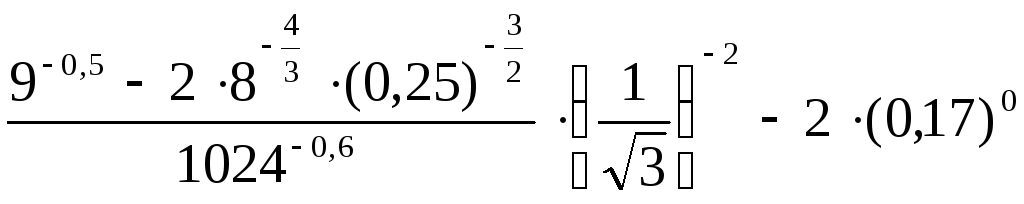 .
.
13.
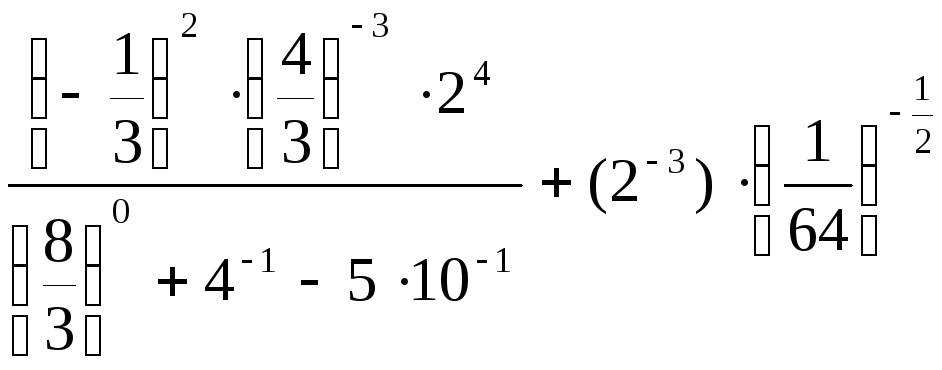 .
.
14.
![]() .
.
15.
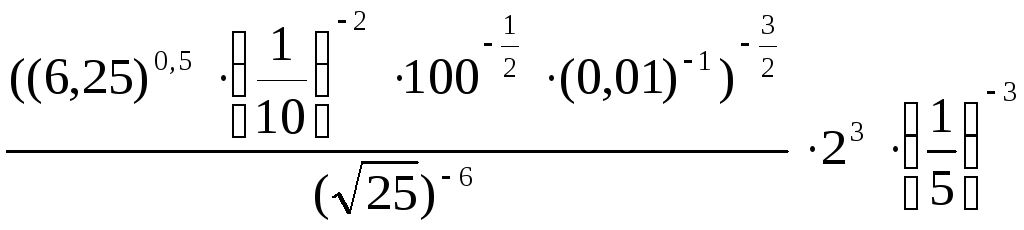 .
.
16.
![]() .
.
17.
 .
.
18.
![]() .
.
19.
![]() .
.
20.
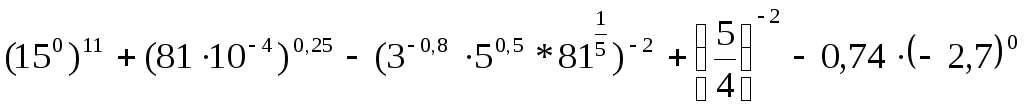 .
.
21.
![]() .
.
22.
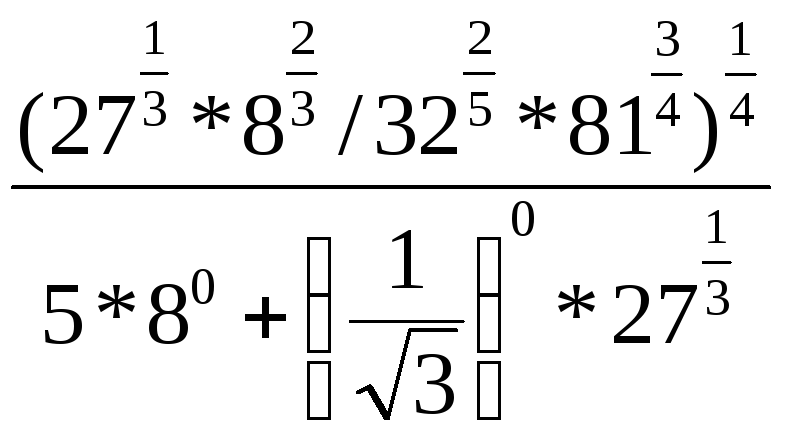 .
.
23.
![]()
24.
![]()
25.
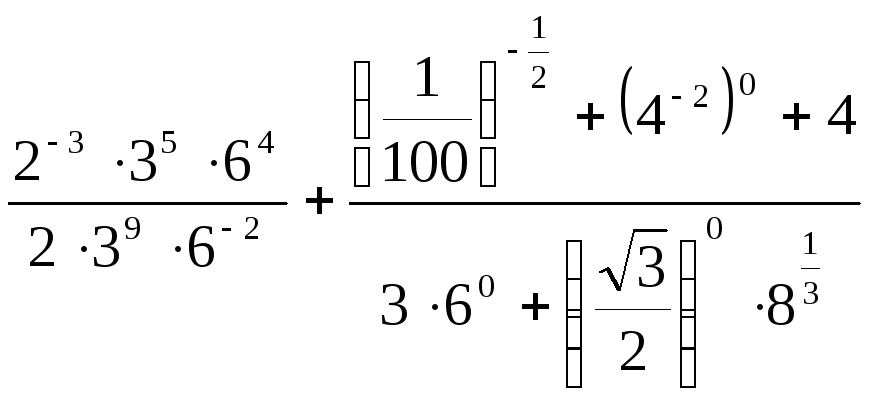
Задание 3. Упростить выражения
1.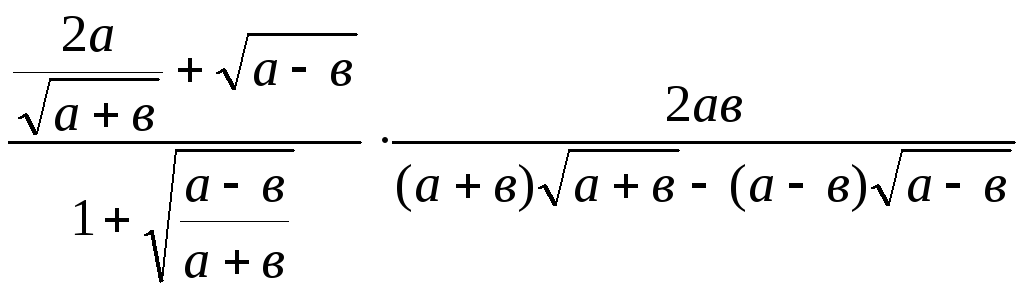 .
.
2.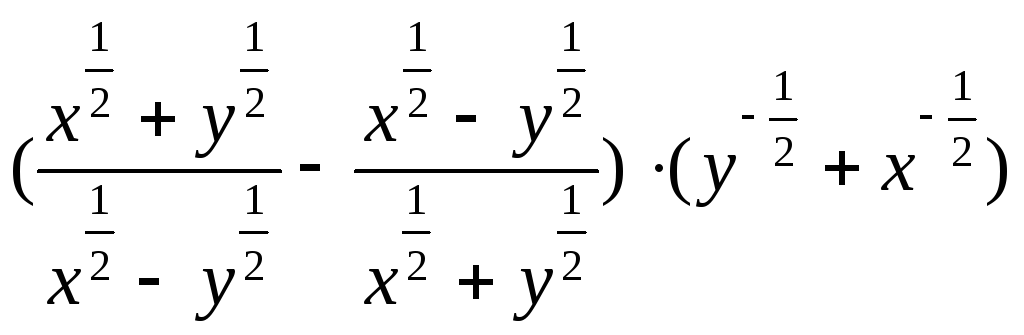 .
.
3.![]() .
.
4.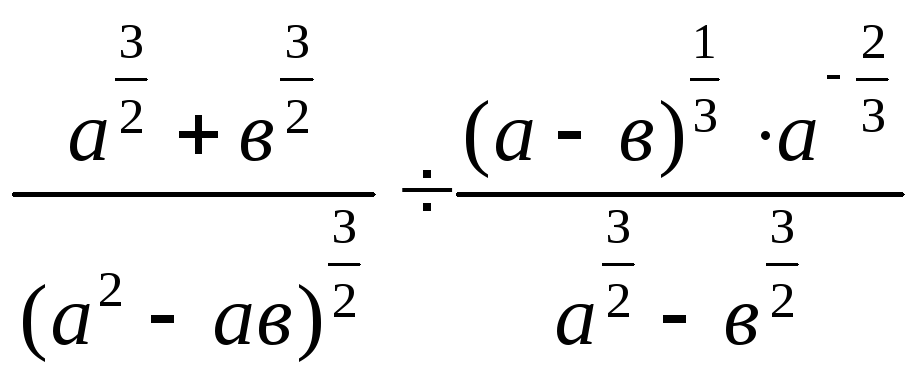 .
.
5.![]()
![]() .
.
6.![]() .
.
7.![]() .
.
8.![]() .
.
9.![]() .
.
10.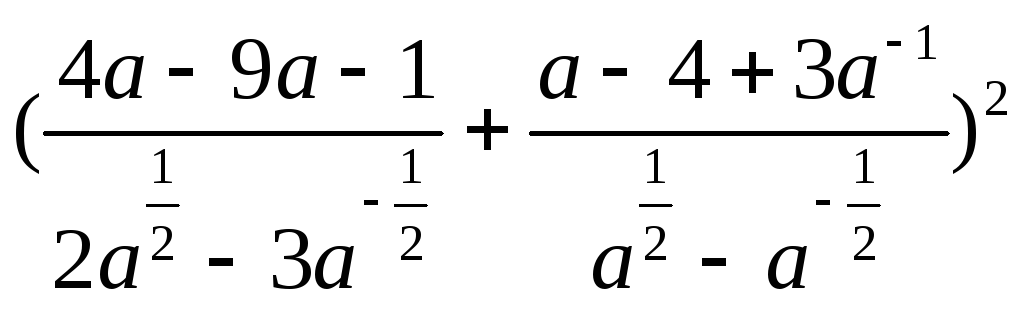 .
.
11.![]() .
.
12.![]() .
.
13.![]() .
.
14.![]() <a<1.
<a<1.
15.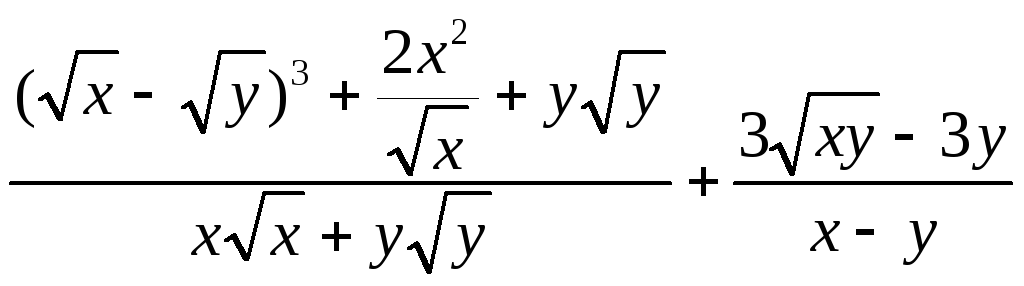 .
.
16.![]() .
.
17. .
.
18.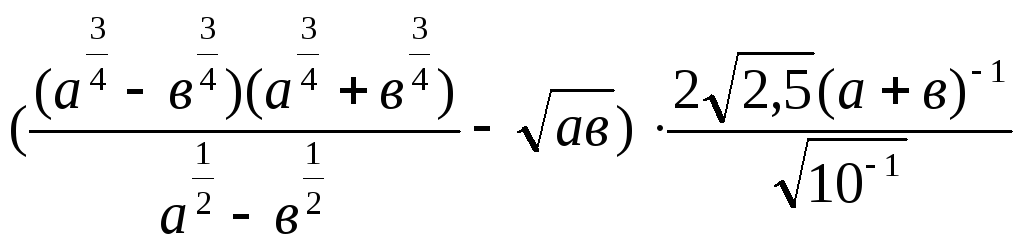 .
.
19.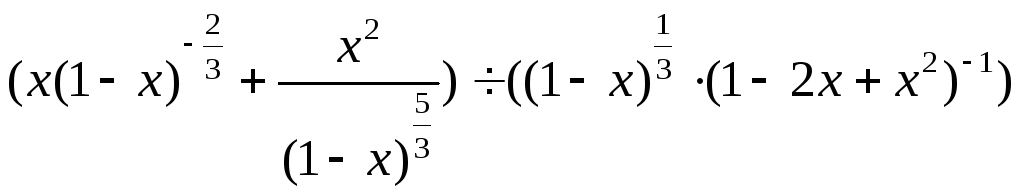 .
.
20.![]() .
.
21.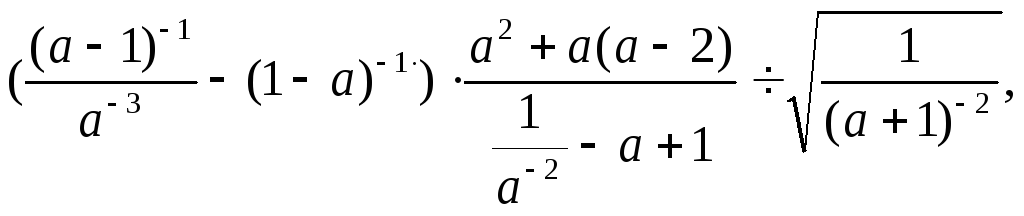 а>0.
а>0.
22.![]() .
.
23.![]() .
.
24.![]() ,
а>0.
,
а>0.
25.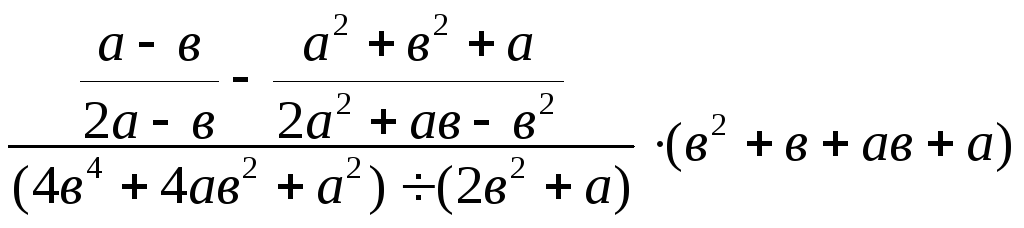 .
.
Задание 4. Решить уравнение
-
 .
.
2.
![]() .
.
3.
![]() .
.
4.
![]()
![]()
![]() .
.
5.
![]() .
.
6.
![]() .
.
7.
![]() .
.
-
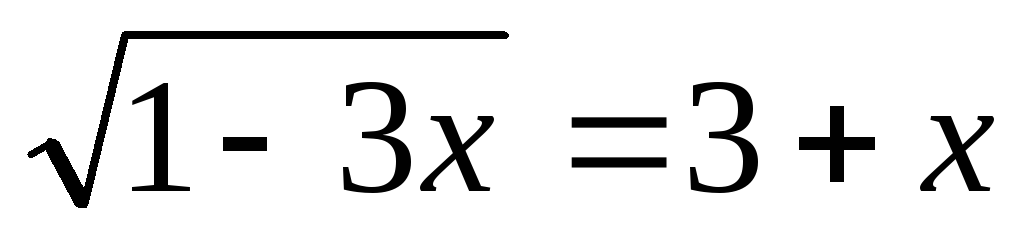 .
.
9.
![]() .
.
10.
![]() .
.
11.
![]() .
.
12.
![]() .
.
13.
![]() .
.
14.
![]() .
.
15.
![]() .
.
-
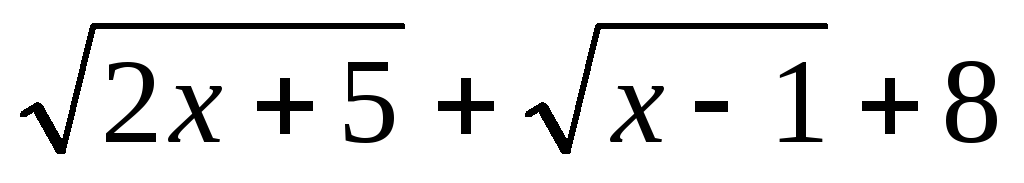
-
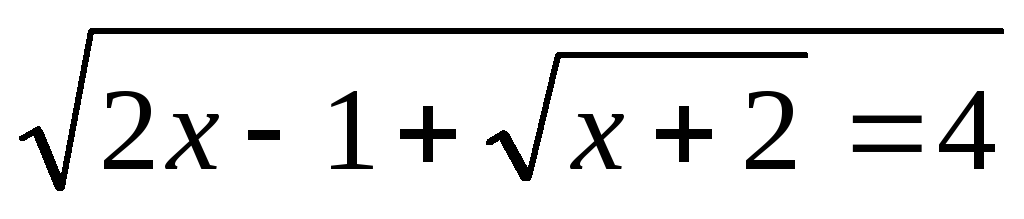 .
. -
 .
. -
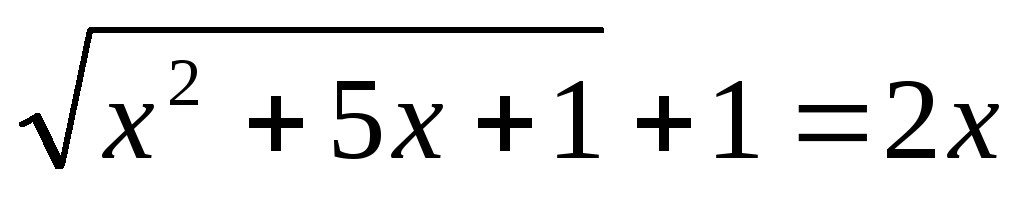 .
. -
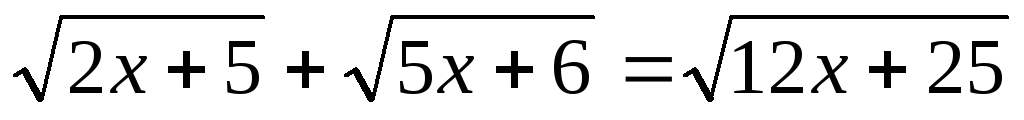 .
. -
 .
. -
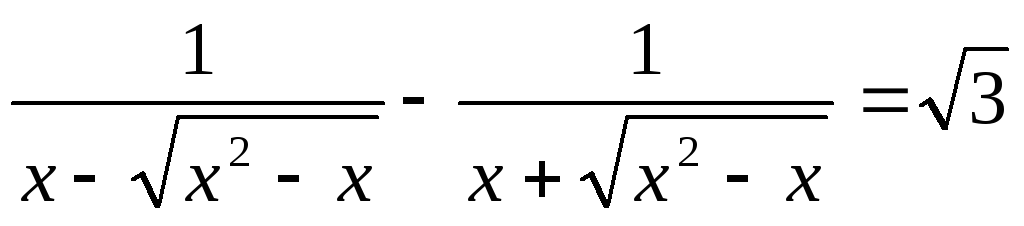 .
. -
 .
. -
 .
. -
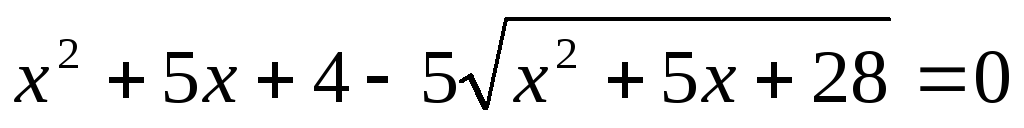 .
.
Задание 5. Решить систему уравнений
1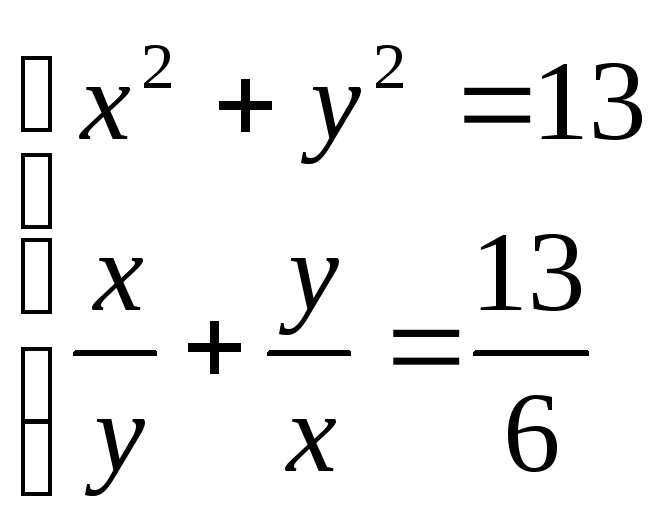 . 2.
. 2.
3.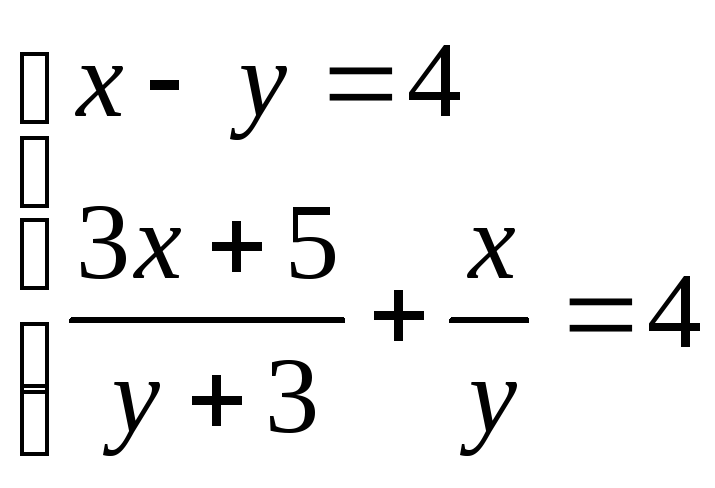 . 4.
. 4.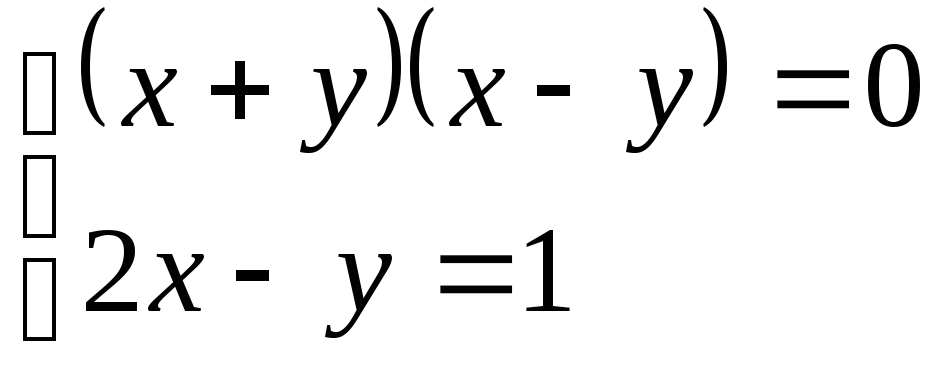 .
.
5. 6.
6.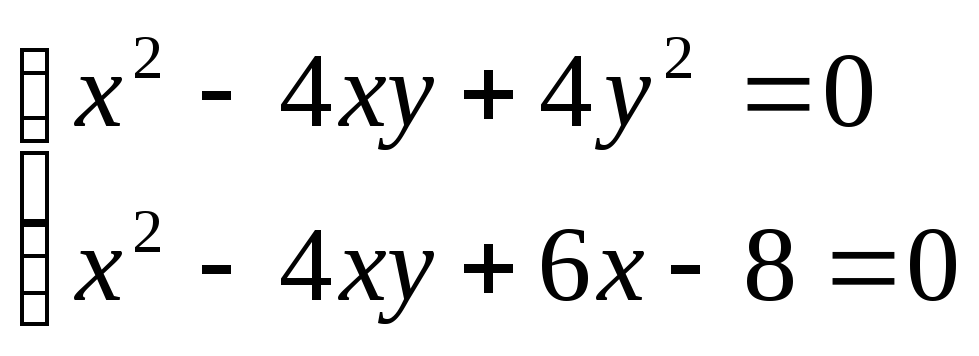 .
.
7.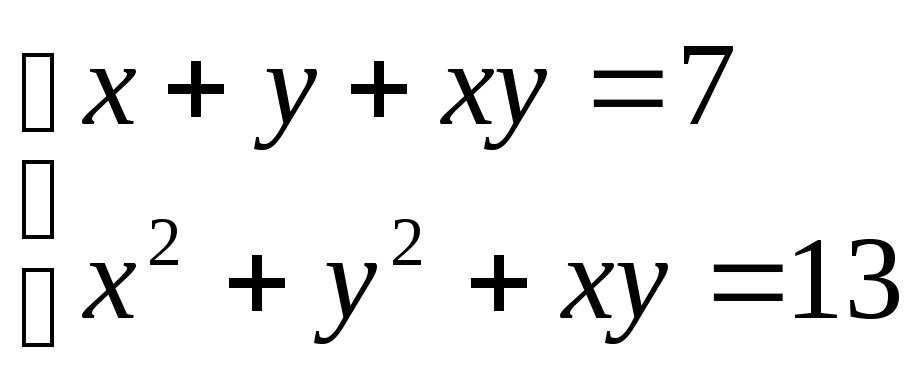 . 8.
. 8.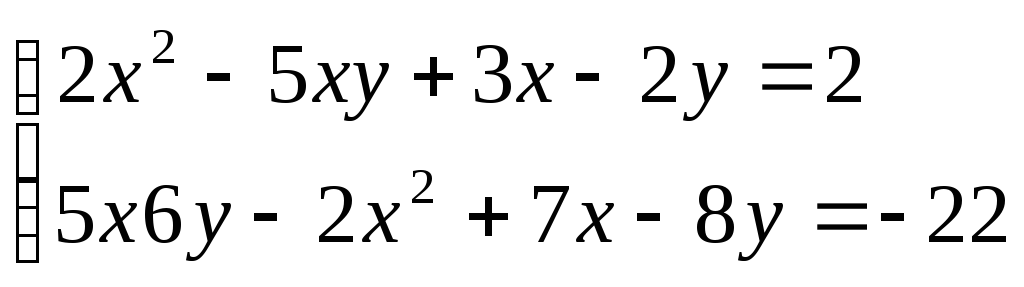 .
.
9.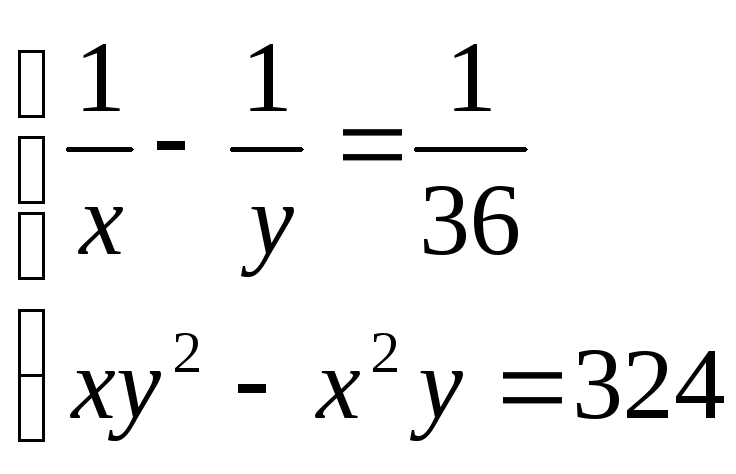 . 10.
. 10.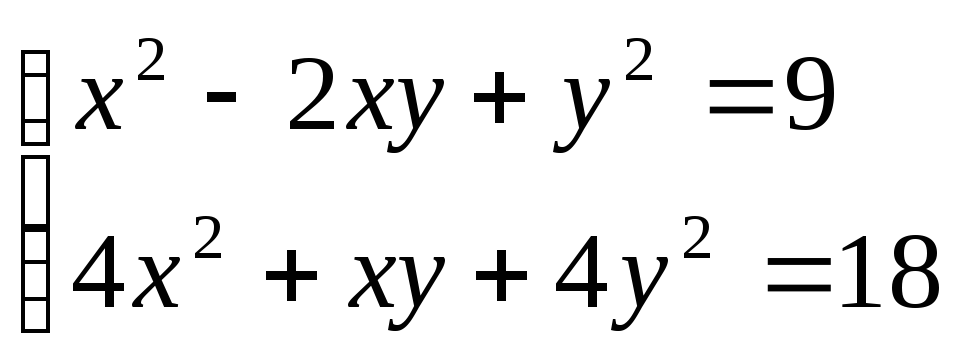 .
.
11.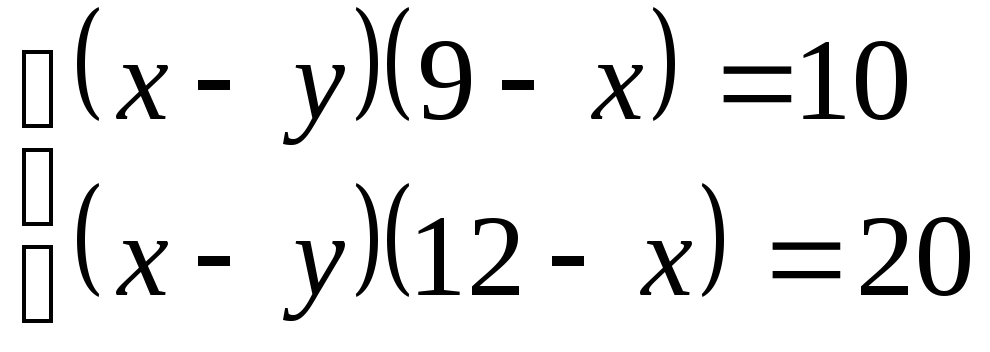 . 12.
. 12.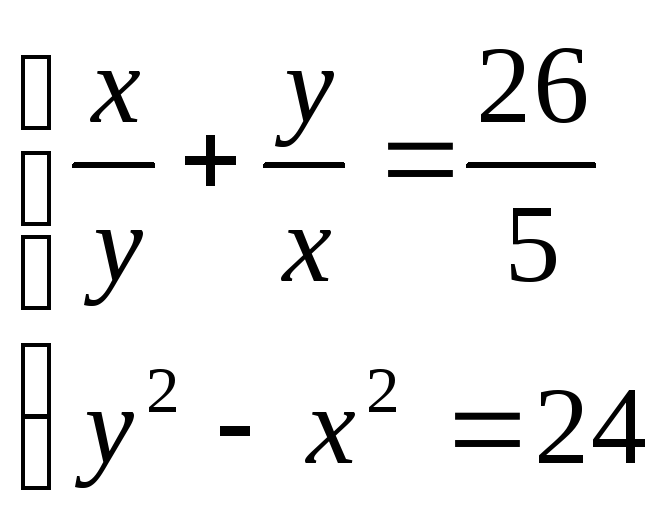 .
.
13.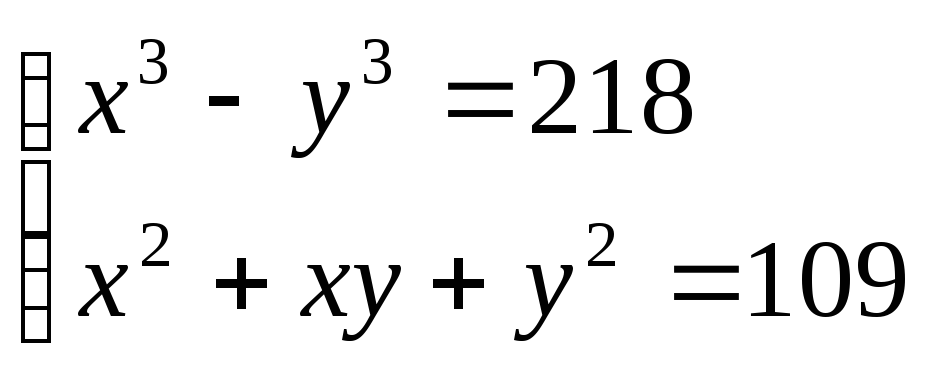 . 14.
. 14.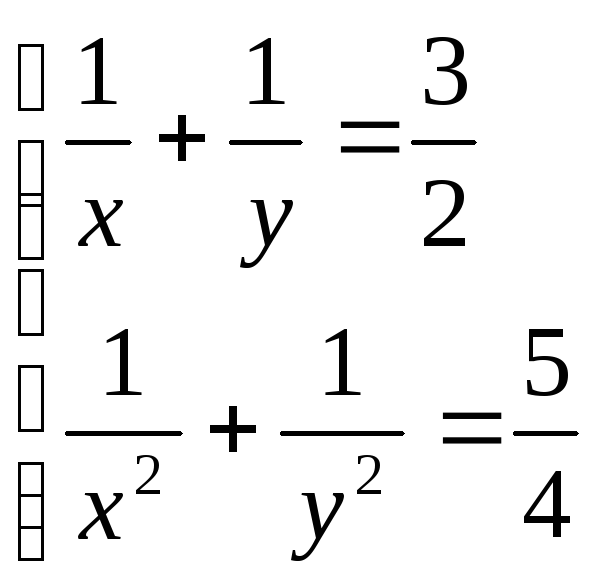 .
.
15. . 16.
. 16.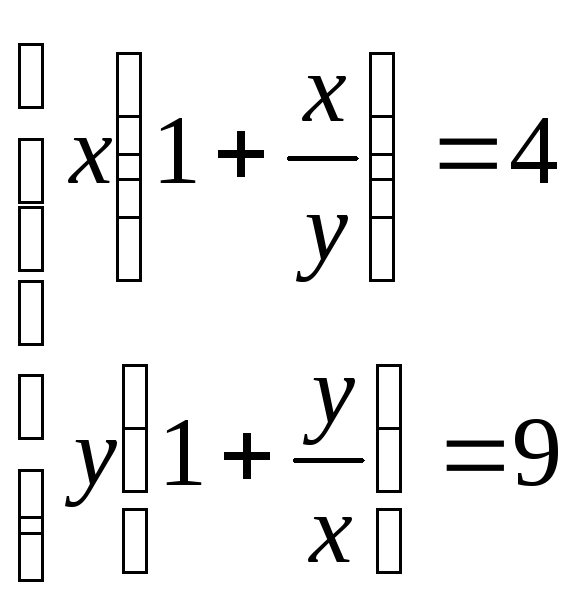 .
.
17.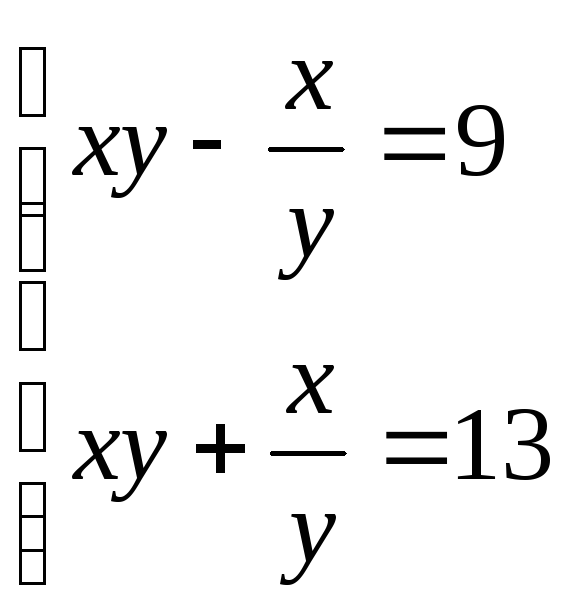 . 18.
. 18. .
.
19.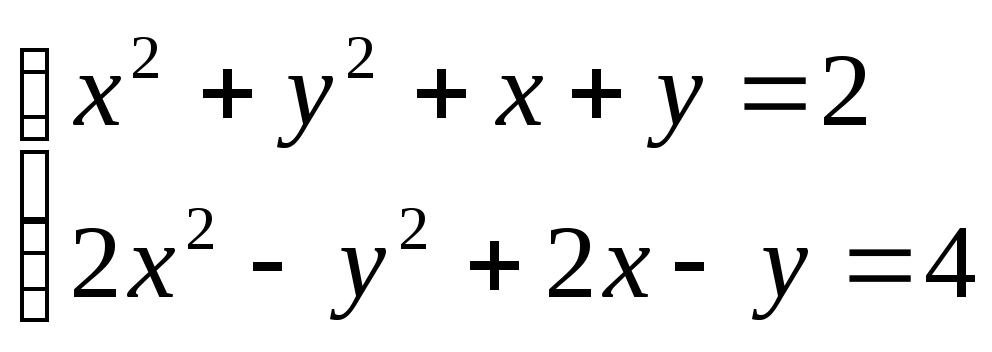 . 20.
. 20.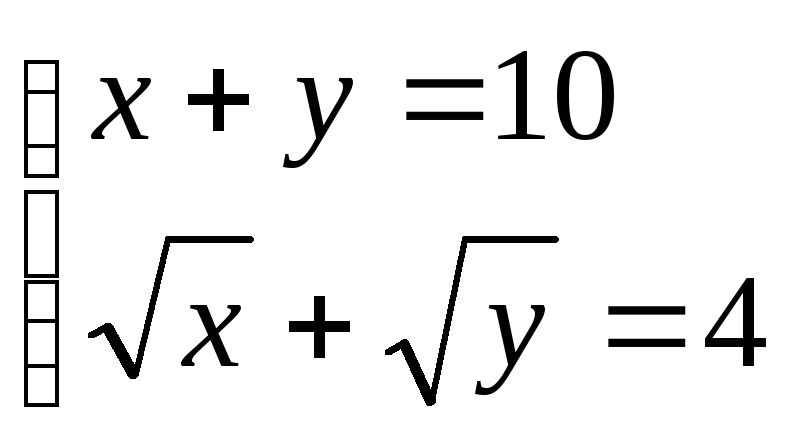 .
.
21.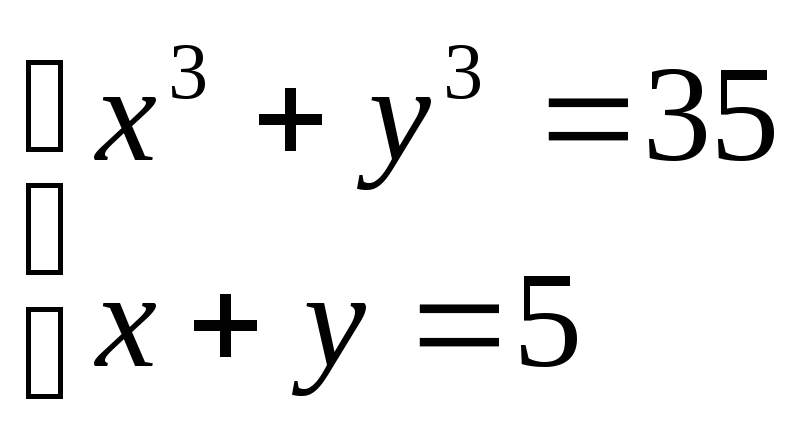 . 22.
. 22.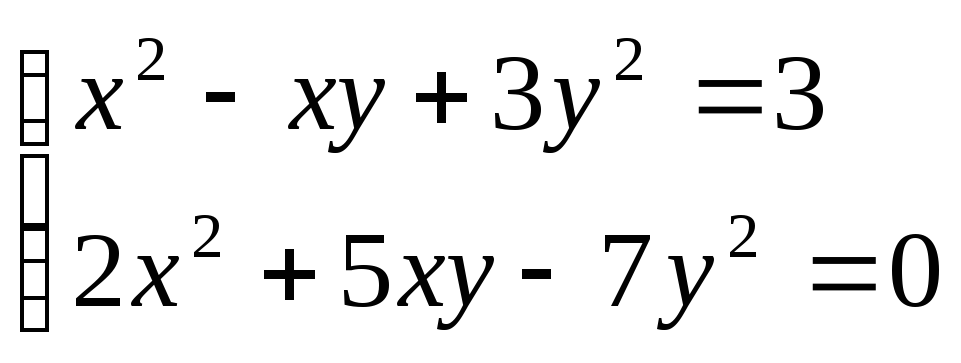 .
.
23. . 24.
. 24.![]() .
.
25.![]() .
.
Задание 6. Решить задачу
-
Один завод выполняет заказ на 4 дня быстрее, чем другой. За какое время может выполнить заказ каждый завод, работая отдельно, если при совместной работе за 24 дня они выполняют заказ в 5 раз больший?
-
В колхозе засеяно 960 га земли; пшеницей – в 2 раза больше, чем кукурузой и рожью вместе. Сколько земли засеяно отдельно пшеницей, рожью и кукурузой, если рожью засеяно на 120 га больше, чем кукурузой?
-
Число десятков двузначного числа втрое больше числа единиц. Если цифры этого числа переставить, то получится число, меньше искомого на 36. Найти число.
-
Две бригады, работая одновременно, обработали участок земли за 12 часов. За какое время могла бы обработать этот участок каждая бригада в отдельности, если скорости выполнения работы бригадами относятся как 2:3?
-
Сумма первых трех членов пропорции равна 58. Третий член составляет 2/3, а второй ¾ первого члена. Найти четвертый член пропорции.
-
Вес сливок составляет 21 % веса молока, масло составляет 25 % веса сливок. Сколько надо взять молока, чтобы получить 7 кг масла?
-
В зрительном зале клуба было 320 мест. После того, как число мест в каждом ряду увеличили на 4 и добавили еще 1 ряд, в зале стало 420 мест. Сколько рядов в зрительном зале?
-
Сумма цифр двузначного числа равна 12. Если цифры его переставить, то получится число больше искомого на 18. Найти число.
-
Сумма цифр двузначного числа равна 11. Если к этому числу прибавить 63, то получится число, записанное теми же цифрами в обратном порядке. Найти это число.
-
Отношение числа рабочих 1 и 2 цехов завода равно соответственно 3:2. Если из 1 цеха перевести 18 рабочих во 2 цех, то отношение станет 5:4. Сколько рабочих в каждом цехе?
-
Сумма квадратов цифр двузначного числа равна 13. Если от этого числа отнять 9, то получится число, записанное теми же цифрами, но в обратном порядке. Найти число.
-
Автомобиль прошел путь от города до деревни со скоростью 60 км/ч. 75 % обратного пути он прошел с прежней скоростью, а остальной путь со скоростью 40 км/ч и затратил на обратный путь на 10 мин. больше. Найти расстояние от города до деревни.
-
Колонна демонстрантов движется по улице со скоростью 3 км/ч. Велосипедист, двигаясь со скоростью 15 км/ч навстречу колонне, употребил 2 мин., для того чтобы проехать от начала до конца колонны. Определить длину колонны.
-
Два экскаватора вырыли яму за 12 дней. Первый экскаватор один мог бы выполнить эту работу в 1,5 раза быстрее, чем один второй. За сколько дней каждый из экскаваторов мог бы выполнить один всю эту работу?
-
Пароход прошел 100 км по течению реки и 64 км против течения, затратив на это 9 часов. В другой раз он прошёл за это время 80 км по течению и 80 км против течения. Определить скорость парохода в стоячей воде.
-
На прокорм 8 лошадей и 15 коров отпускается ежедневно 162 кг сена. Сколько сена выдавали ежедневно каждой корове и каждой лошади, если 5 лошадей получили на 3 кг сена больше, чем 7 коров?
-
Доска прямоугольной формы имеет площадь, равную 4 500 см2. От нее отрезали прямоугольник той же ширины и длинной 120 см. Оставшаяся часть – квадрат. Найти сторону этого квадрата.
-
Числитель дроби на один больше знаменателя. Если к числителю прибавить 3, а к знаменателю прибавить 18, то получится дробь меньше исходной на 1. Найти исходную дробь.
-
В зрительном зале клуба было 160 мест. При расширении зала число мест в каждом ряду увеличили на 2, а число рядов увеличили на 1. В результате стало на 96 мест больше. Сколько было рядов?
-
Моторная лодка прошла по течению реки 45 км и против течения 22 км, затратив на весь путь 5 часов. Найти скорость лодки в стоячей воде, если скорость течения реки 2 км/ч.
-
Сколько воды нужно выпарить из 500 кг целлюлозной массы, содержащей 85 % воды, чтобы получить массу с содержанием 75 % воды?
-
Найти три числа, если первое составляет 80 % второго, второе относится к третьему как 0,5:9/20, а сумма первого и третьего на 70 больше второго числа.
-
В двух бидонах находится 70 литров молока. Если из 1 бидона перелить во 2-й 12,5 % молока, находящегося в 1 бидоне, то в обоих бидонах будет поровну. Сколько молока в каждом бидоне?
-
Найти сумму трех чисел, зная, что Ш:1,4,5:3, Ш составляет 40 % П, а сумма 1и 2 равна 400.
-
Свежие грибы содержат по весу 90 % воды, а сухие 12 %. Сколько получится сухих грибов из 22 кг свежих?
Задание 7. Решить неравенство
-
(x2-1)(x+3)<0.
-
(1-x2)(x+3)>0.
-
(x-3)2(x2-25)≥0.
-
(x+3)(x2-9)<0.
-
(x+3)(x2-16)≤0.
-
x2>3.
-
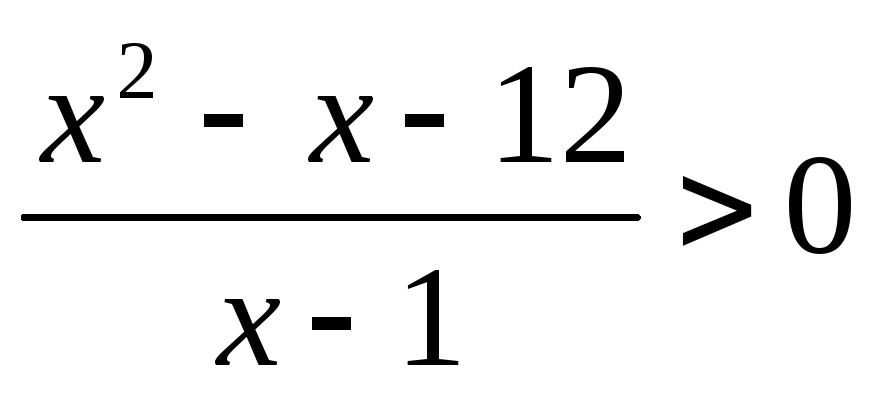 .
. -
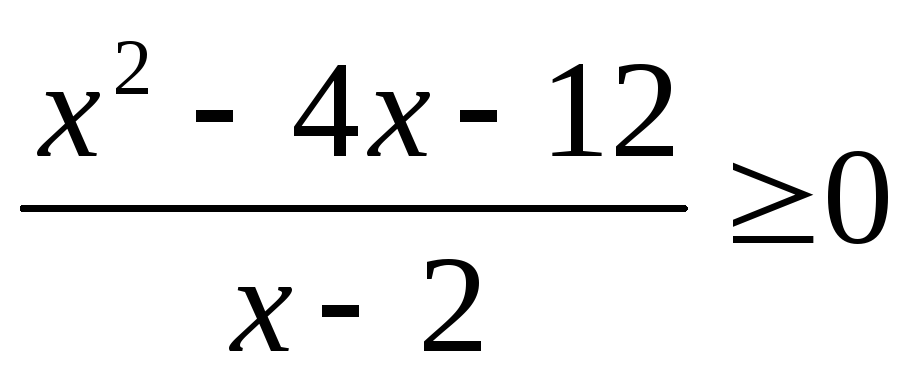 .
. -
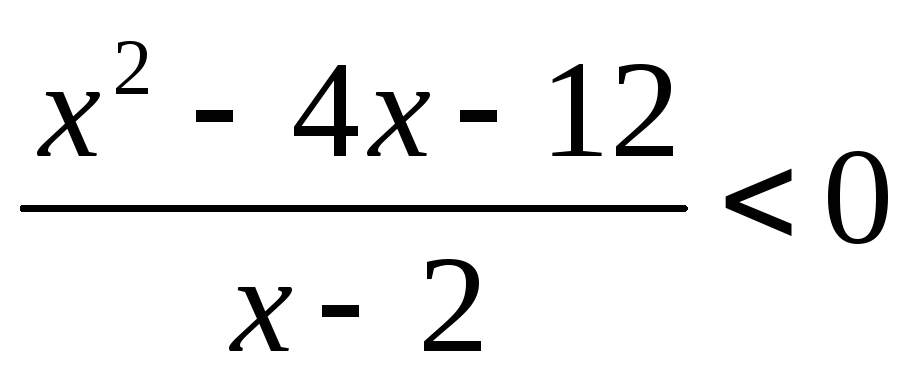 .
. -
 .
. -
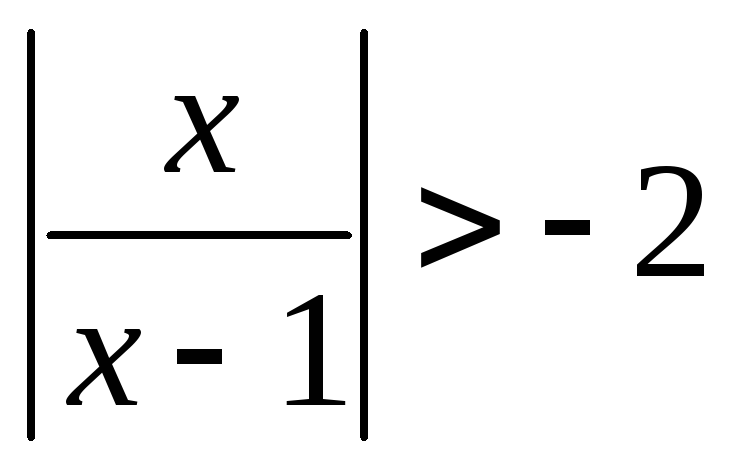 .
. -
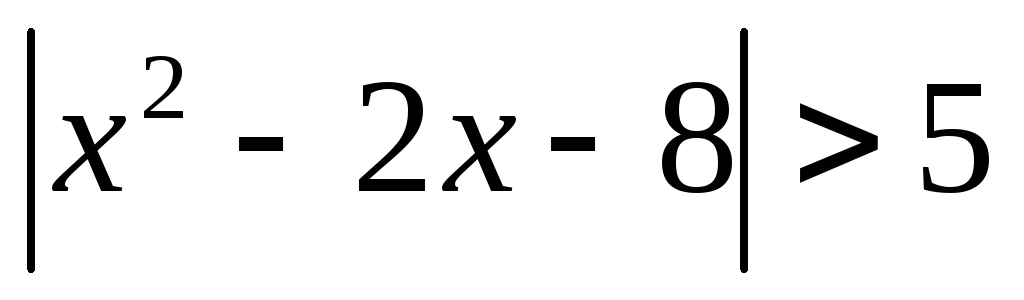 .
. -
 .
. -
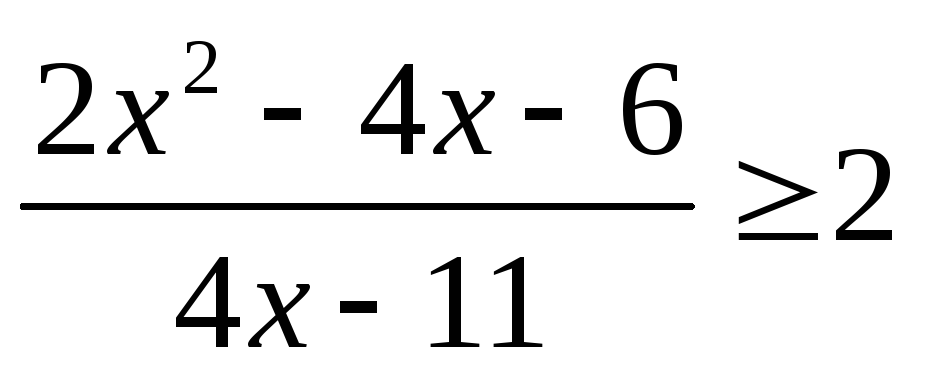 .
. -
(x2+1)(x2+x+1)(x+5)3>0.
-
(x+4)2(x+5)2(x-6)(x+3)≤0.
-
x2+x+
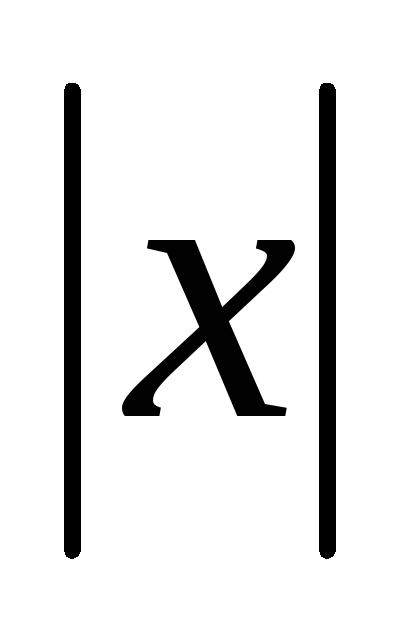 +1≤0.
+1≤0. -
x2-4
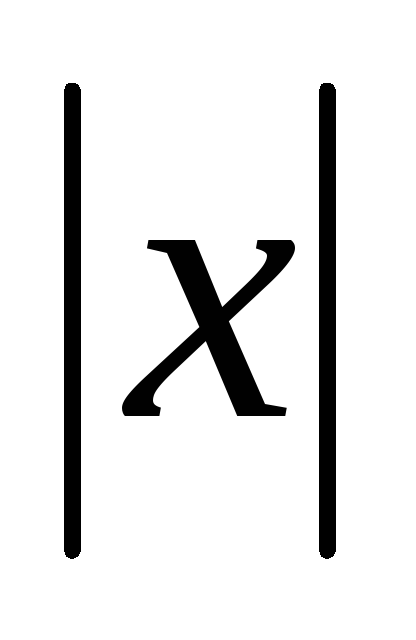 +3>0.
+3>0. -
 .
. -
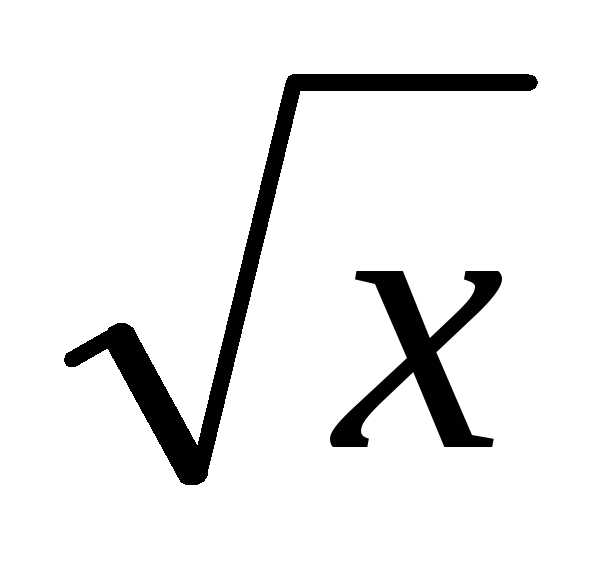 (x+2)>0.
(x+2)>0. -
 (x-2)<0.
(x-2)<0. -
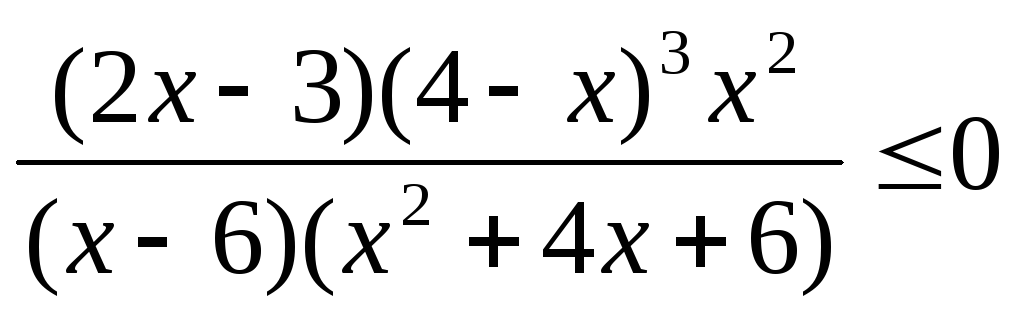 .
. -
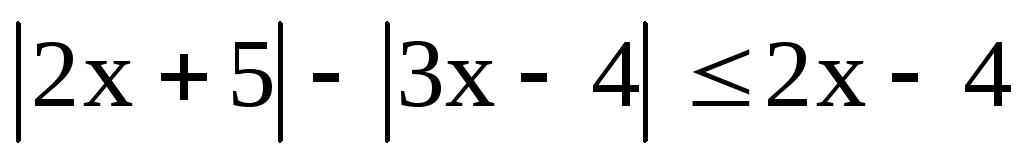 .
. -
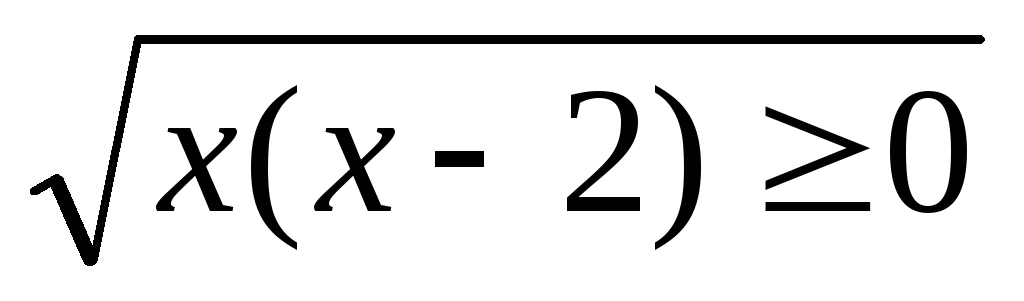 .
. -
x2-5x≥0.
Задание 8. Решить уравнение
1.
![]() . 2.
. 2.
![]() .
.
3.
![]() .
4.
.
4.
![]() .
.
5.
![]() .
6.
.
6.
![]() .
.
7.
![]() .
8.
.
8.
![]() .
.
9.
![]() .
10.
.
10.
![]() .
.
11.
![]() .
.
12.
![]()
![]() .
13.
.
13.
![]() .
.
14.
![]() .
15.
.
15.
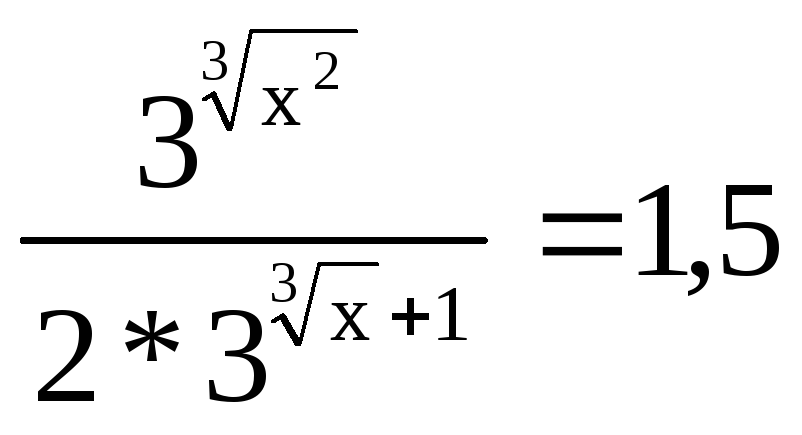 .
.
16.
![]() .
17.
.
17.
![]()
![]() .
.
18.
![]() .
19.
.
19.
![]() .
.
20.
![]() .
21.
.
21.
![]() .
.
22.
![]() .
23..
.
23..
![]() .
.
24.
![]() .
25.
.
25.
![]() .
.
Задание 9. Решить уравнение
-
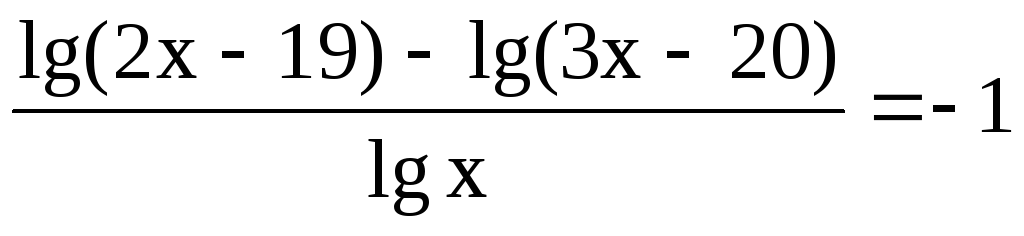 .
. -
lg
 =
= .
.
-
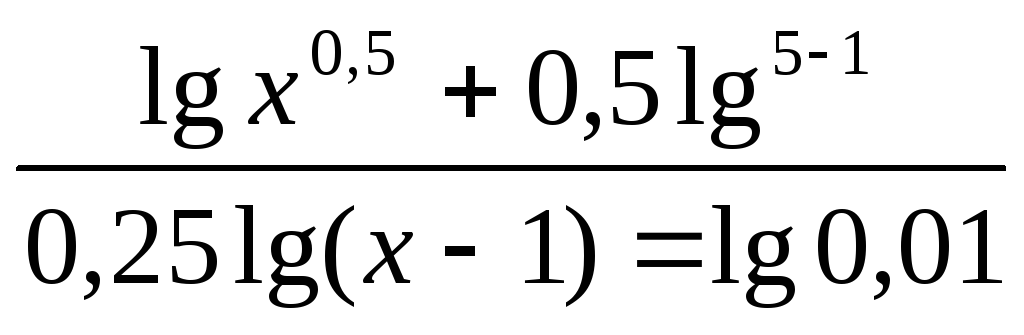 .
. -
lg
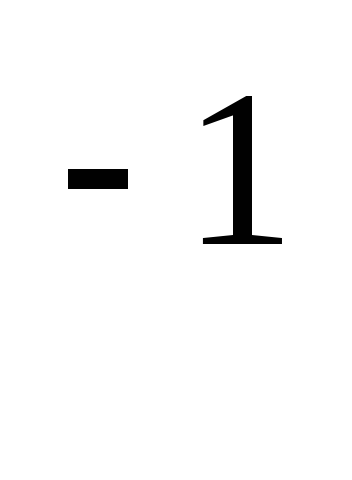 x=6-lg
x=6-lg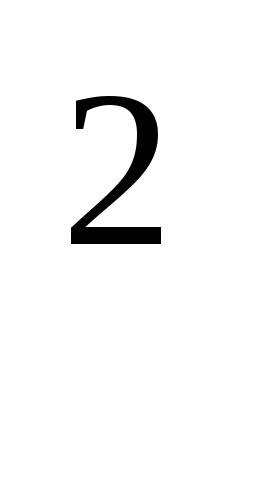 100+lgx
100+lgx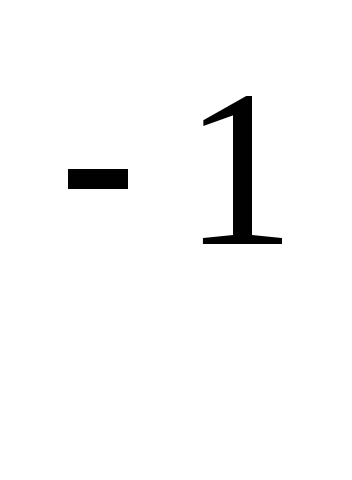 .
. -
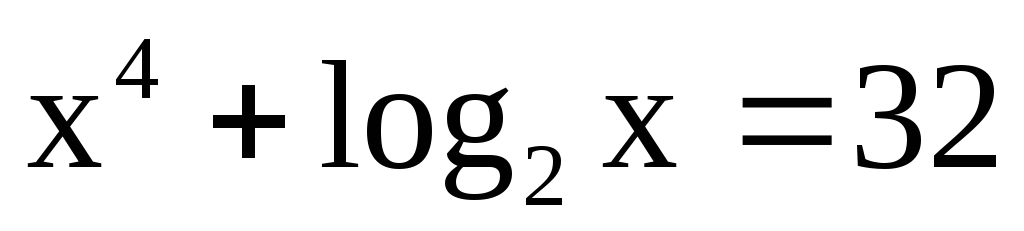
 .
. -
log
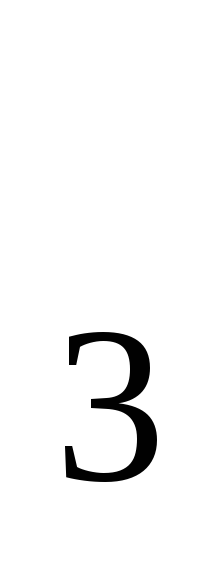 (3
(3 +1)-log
+1)-log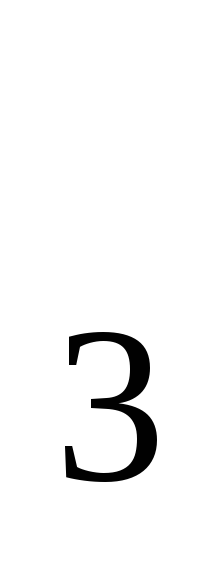 (1-3
(1-3 )-2x=log
)-2x=log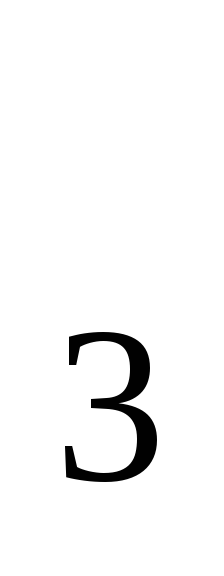 (
( .
. -
log
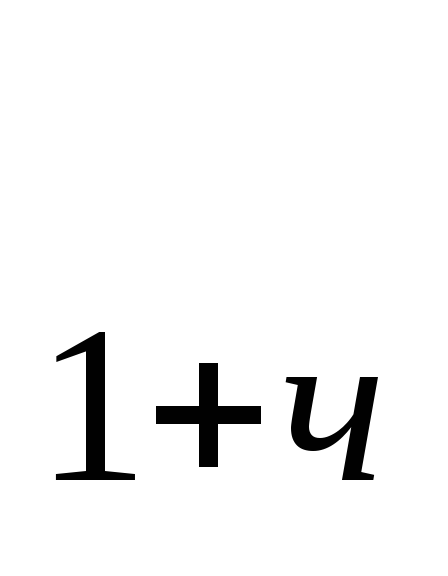 (2x
(2x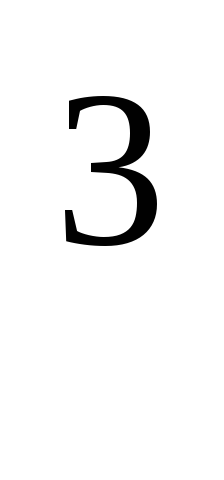 +2x
+2x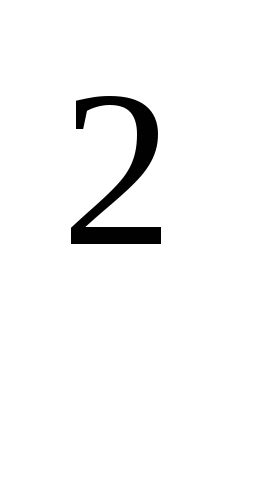 -3x+1)=3.
-3x+1)=3. -
2lg2+lg(5
 +1)=2+lg(5
+1)=2+lg(5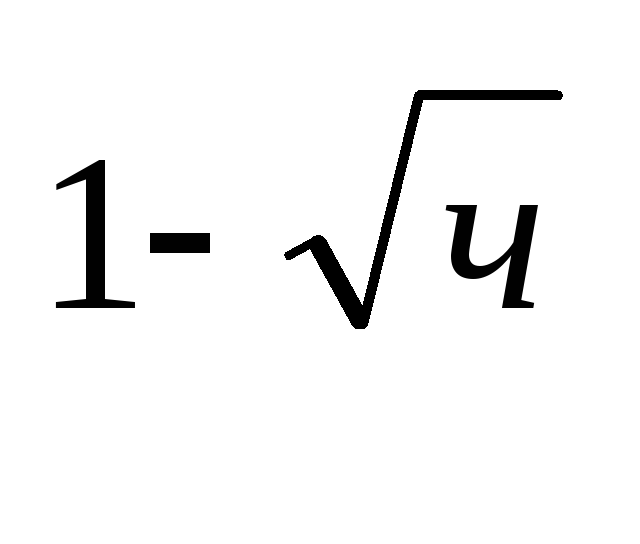 +5).
+5). -
lg
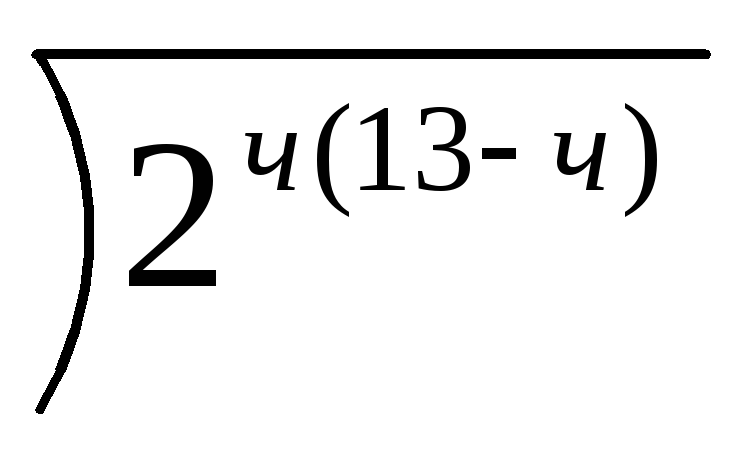 +11lg5=11.
+11lg5=11. -
 lg(3
lg(3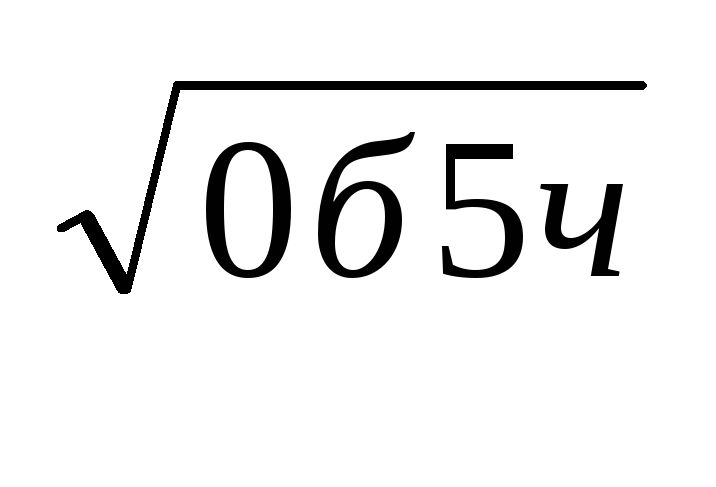 +73)+lg10=2.
+73)+lg10=2. -
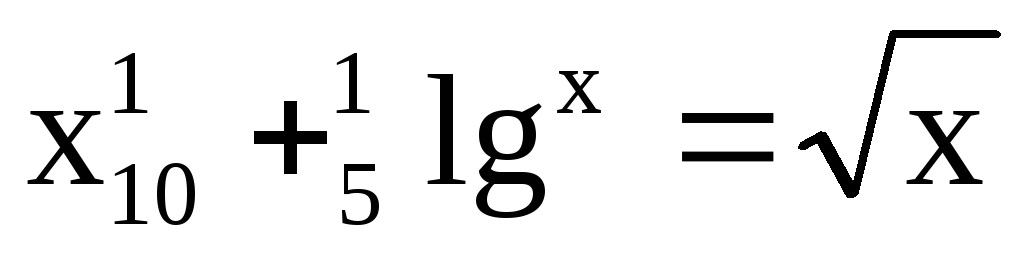 .
. -
2lglgx=lg(3-2lgx).
-
2x-lg(25
 +4x-16)=lg4
+4x-16)=lg4 .
. -
lg(2
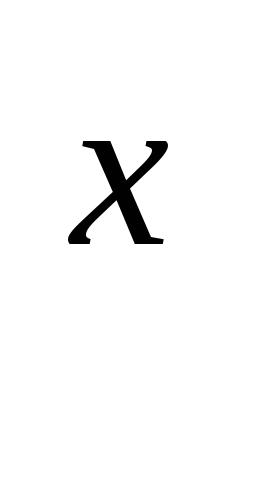 +x-41)=x(1-lg5).
+x-41)=x(1-lg5). -
lg
 -3lg
-3lg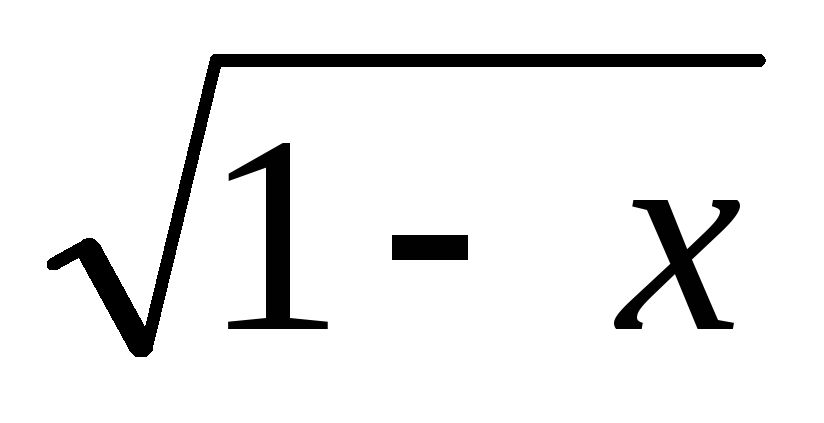 =lg
=lg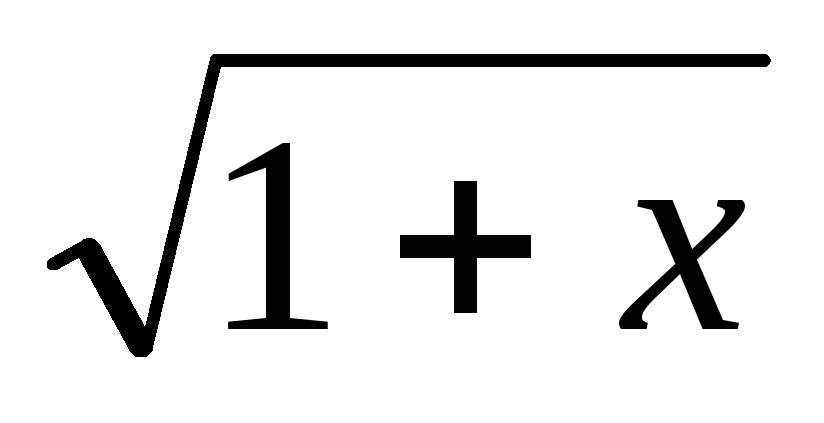 +2.
+2. -
lg
 (x-1)-1,25
lg
(x-1)-1,25
lg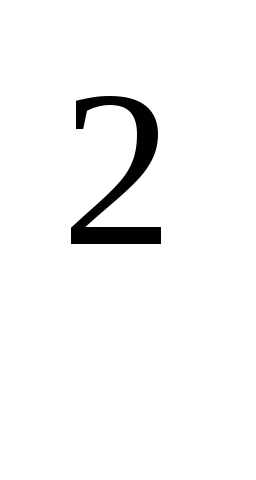 (x-1)=
- 4.
(x-1)=
- 4. -
log

 +
+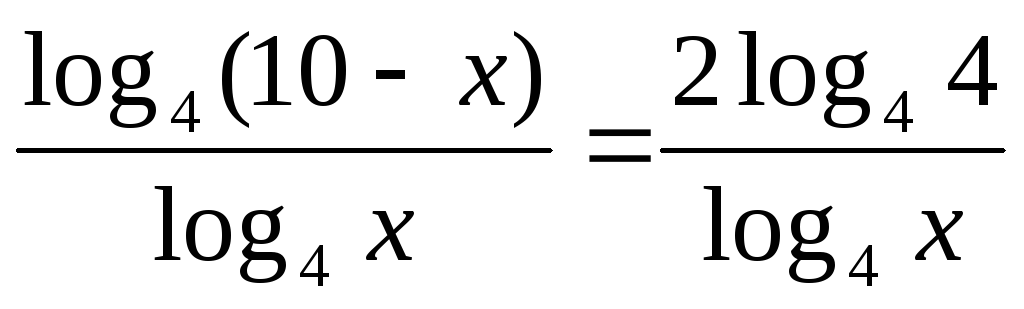 .
. -
(log
 5+2)log
5+2)log x=1.
x=1. -
log

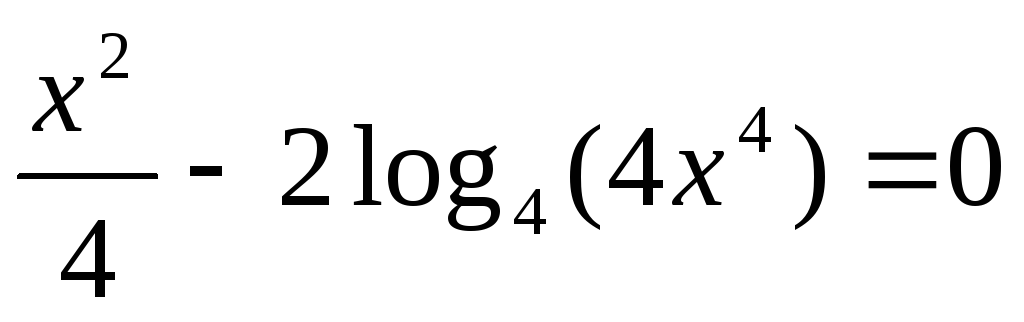 .
. -
(1+
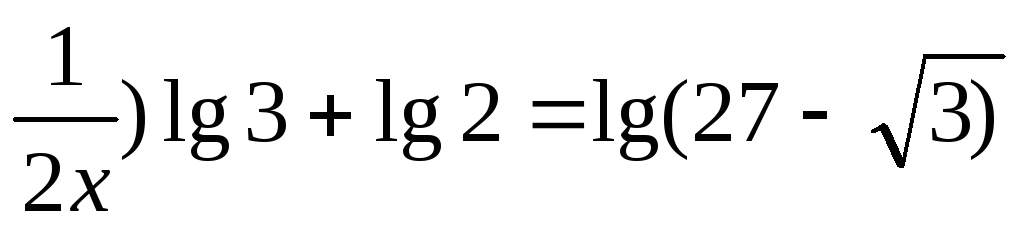 .
. -
lg10+
 .
. -
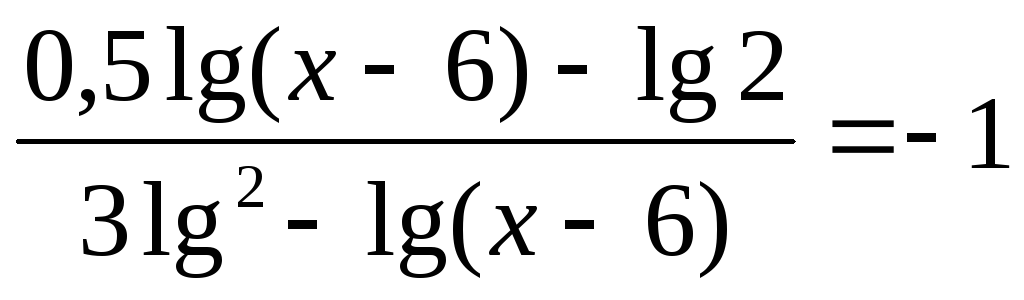
 .
. -
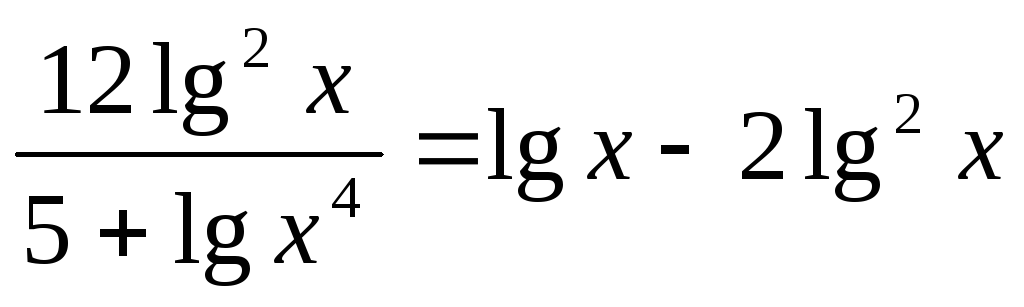 .
. -
lg(lgx)+lg(lgx
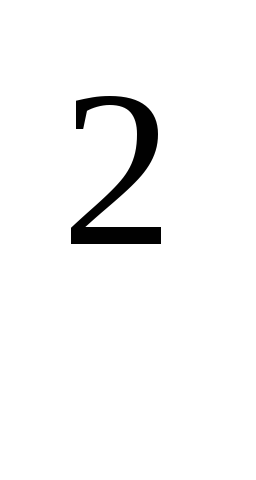 -1)=1.
-1)=1. -
3
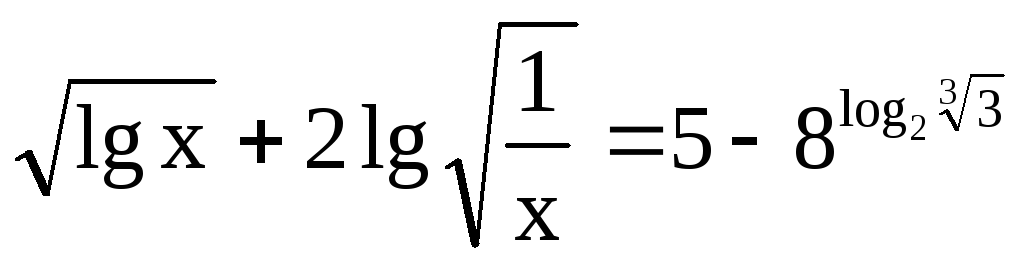 .
.
Задание 10. Решить неравенство
1.
![]() . 2.
. 2.
![]() .
.
3.
![]() . 4.
. 4.
![]() .
.
5.
![]() . 6.
. 6.
![]() .
.
7.
![]() . 8.
. 8.
![]() .
.
9.
![]() . 10.
. 10.
![]() .
.
11.
![]() . 12.
. 12.
![]() .
.
13.
![]() . 14.
. 14.
![]() .
.
15.
![]() . 16.
. 16.
![]() .
.
17.
![]() . 18.
34ч+8-4·32ч+5
<-27.
. 18.
34ч+8-4·32ч+5
<-27.
19. 3x(x2-2x-3)<9x2-18x-27. 20. 2x+1-22x+1+16≥0.
21. (0,2)![]() >25. 22.
81x-1-52x-2-4·92x-3<4·52x-3.
>25. 22.
81x-1-52x-2-4·92x-3<4·52x-3.
23.
![]() >243. 24.
x2·2x+x·2x-1>0.
>243. 24.
x2·2x+x·2x-1>0.
25. 2x+2-2x+3-2x+4>5x+1-5x+2.
Задание 11. Решить неравенство
-
log16x + log4x + log2x < 7.
-
log0,1
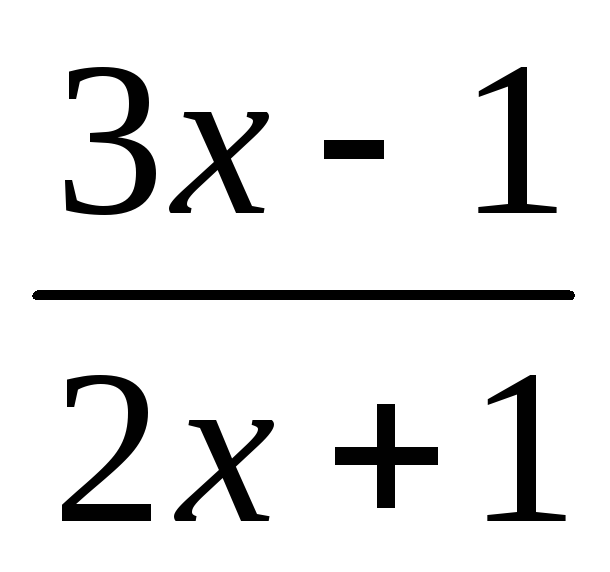
0.
0. -
log3(x-1) – log3(2x-5) > 1.
-
log3(2x-5) < 1.
-
log1/2x + log1/2(x+1) < log1/2(2x+6).
-
2log8(x-2) – log8(x-3) >
 .
. -
log(x+27) – log(16-2x) < logx.
-
log0,3(x2-5x+7) > 0.
-
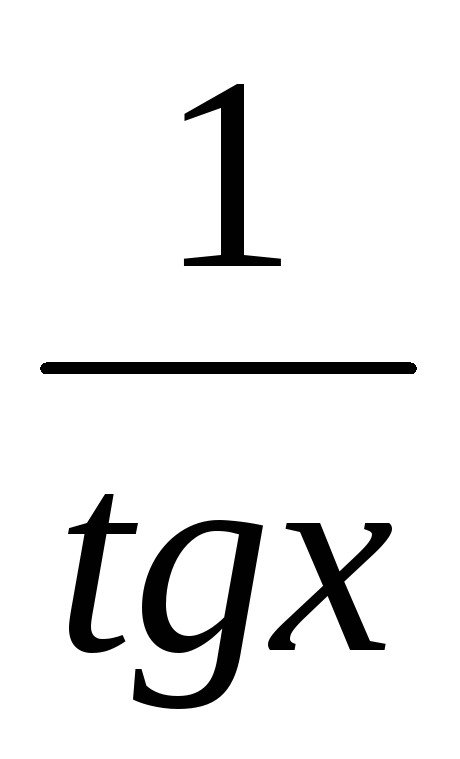 -
-
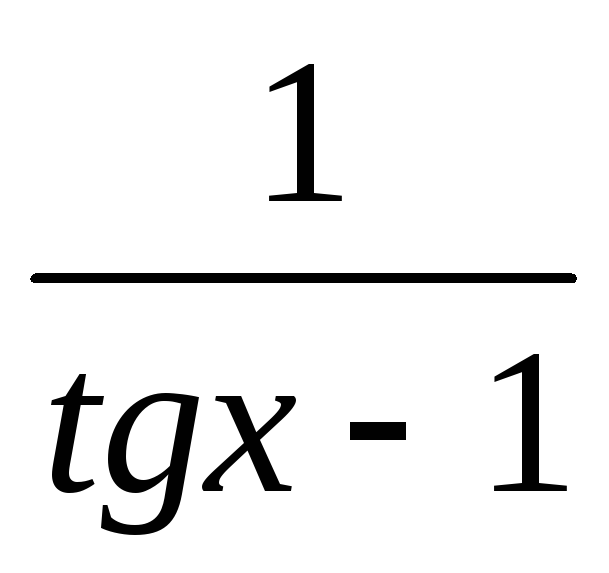 > 1.
> 1. -
log3(x-1)2 – log3(2x-5) > 1.
-
log3log5(25-4x) < 1.
-
lg
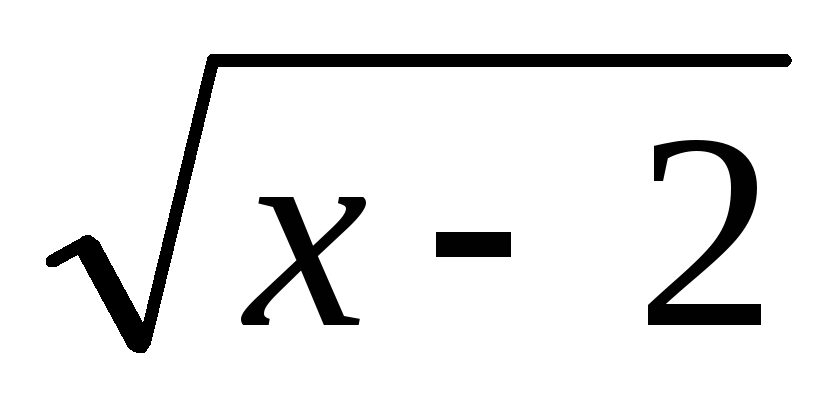 + 0,5lg(3x-5)
>
+ 0,5lg(3x-5)
>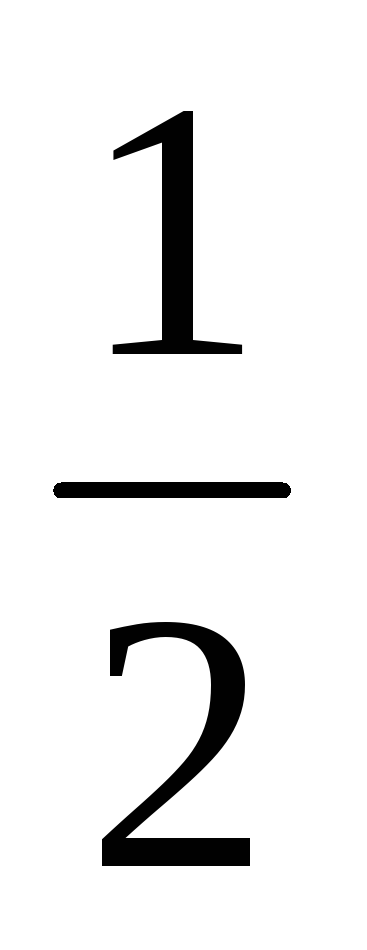 .
. -
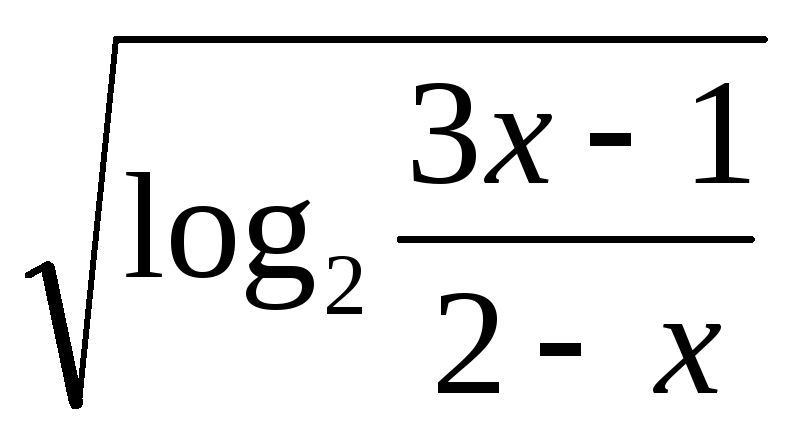 < 1.
< 1. -
log2log1/2(x2+2x-
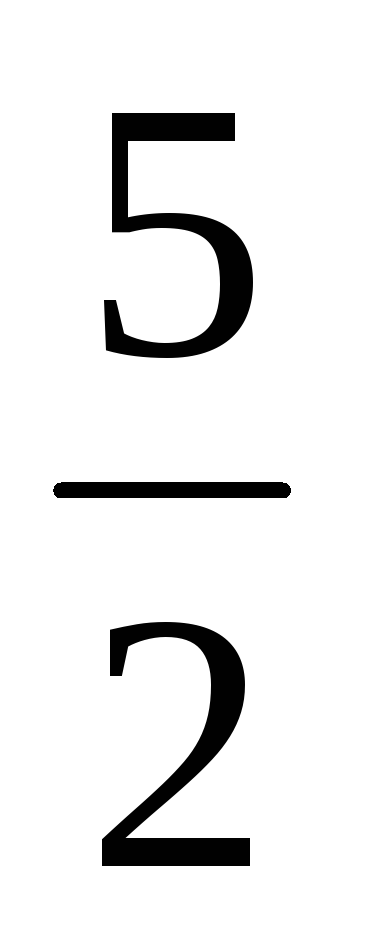 )
< 0.
)
< 0. -
log4(x+7) > log2 (x+1).
-
log2(9x-1+7) > 2+log2(3x-1+1).
-
0,5(lg
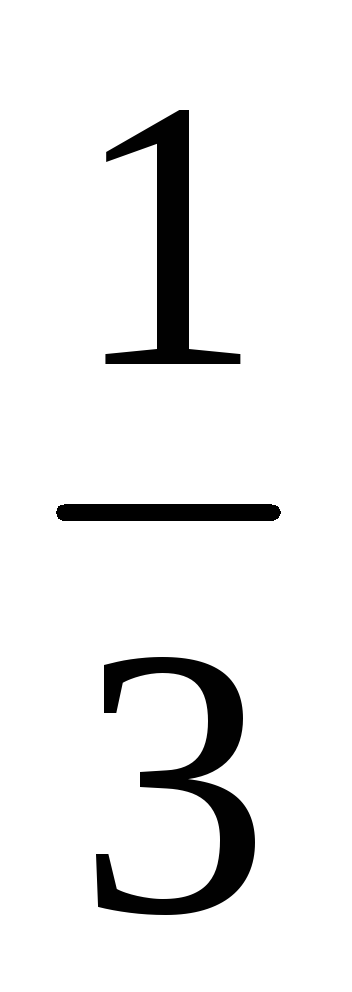 +lgx
+lg
+lgx
+lg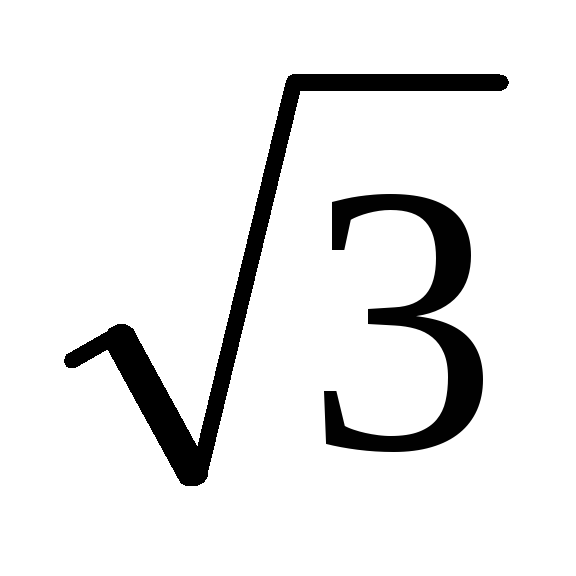 )
1- lg2.
)
1- lg2.
18.![]() .
.
19.![]() .
.
20.![]() .
.
21.![]() .
.
22.
![]() .
.
23.![]() .
.
24.![]() .
.
25.![]() .
.
Задание 12. Упростить выражение
-
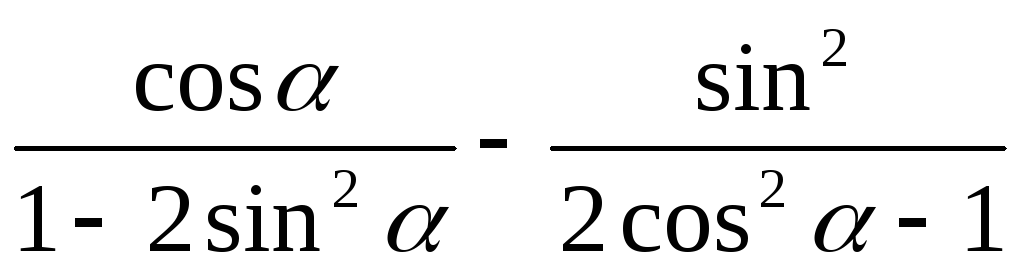 .
. -
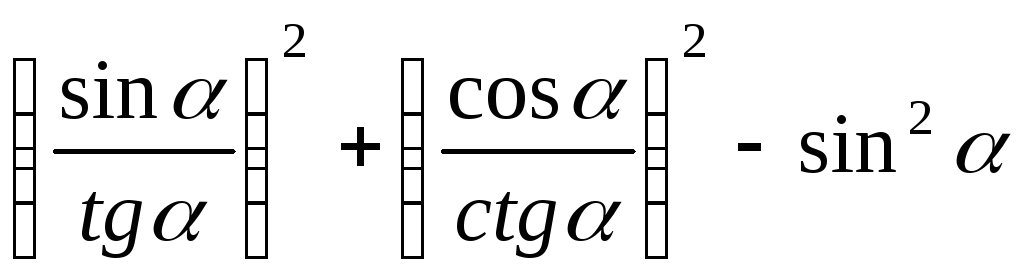 .
. -
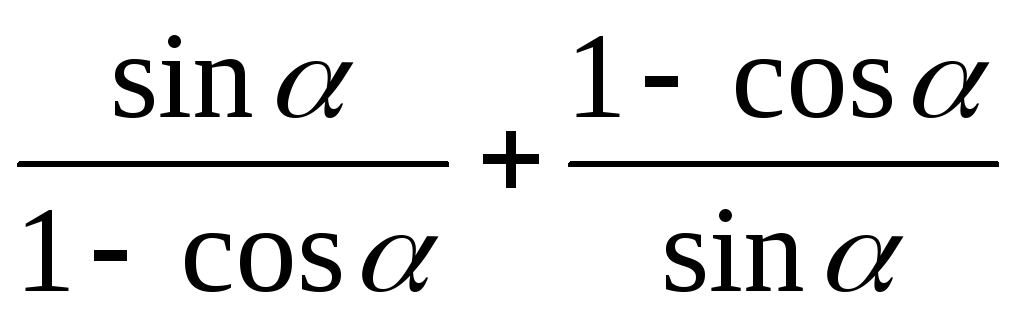 .
. -
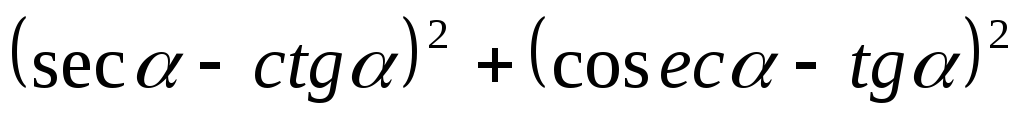 .
. -
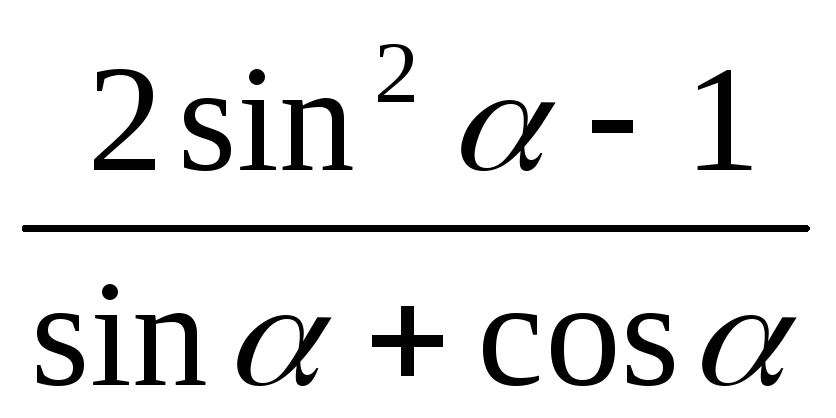 .
. -
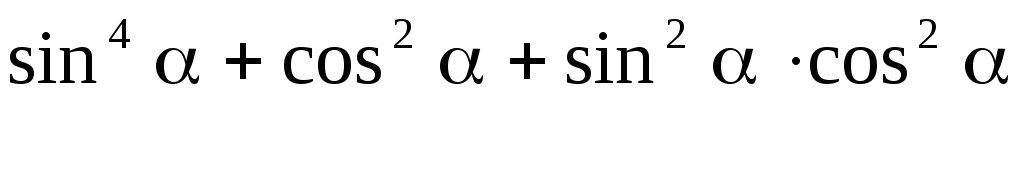 .
. -
 .
. -
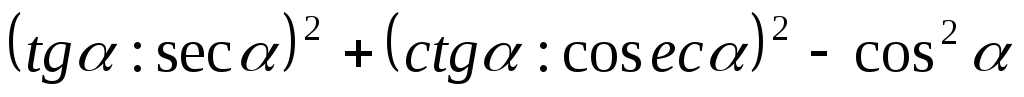 .
. -
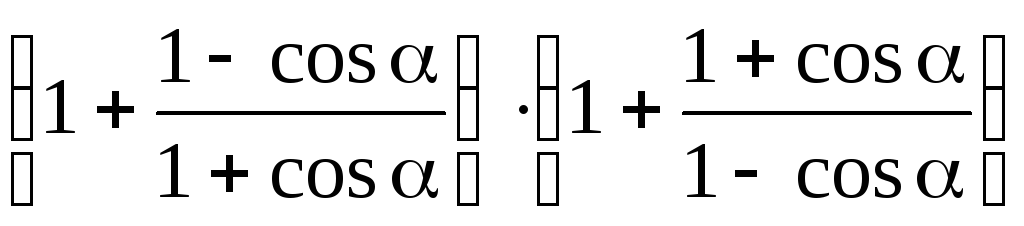 .
. -
 .
. -
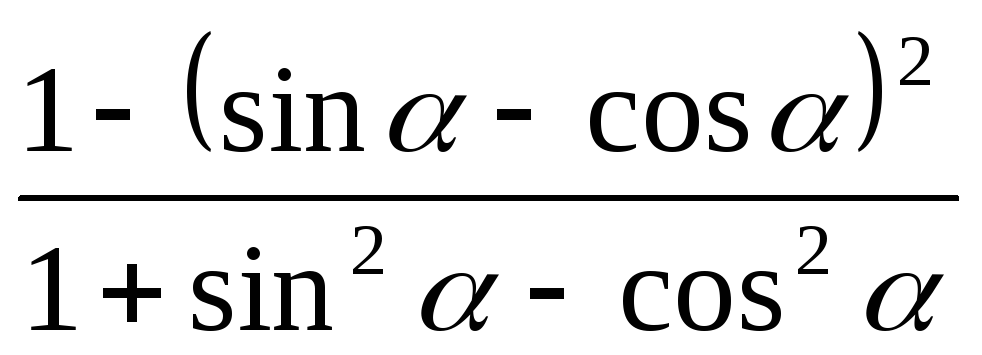 .
. -
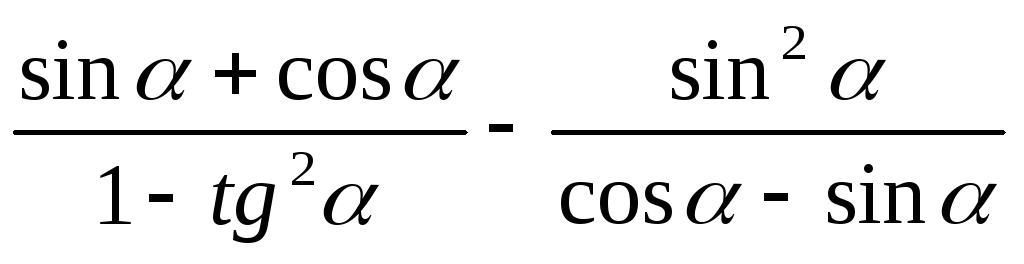 .
.
-
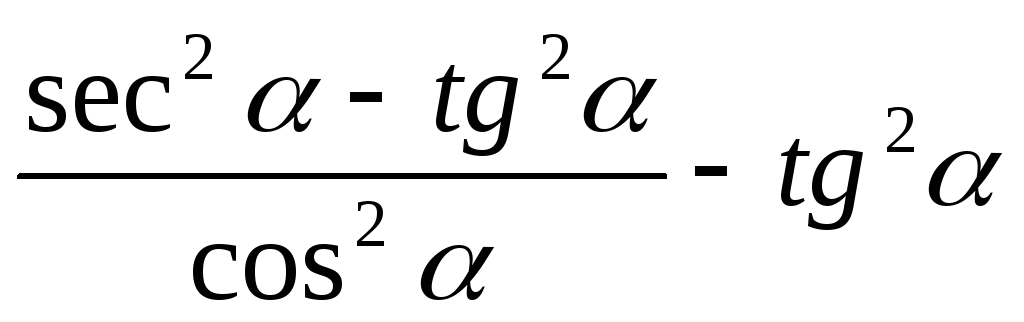 .
. -
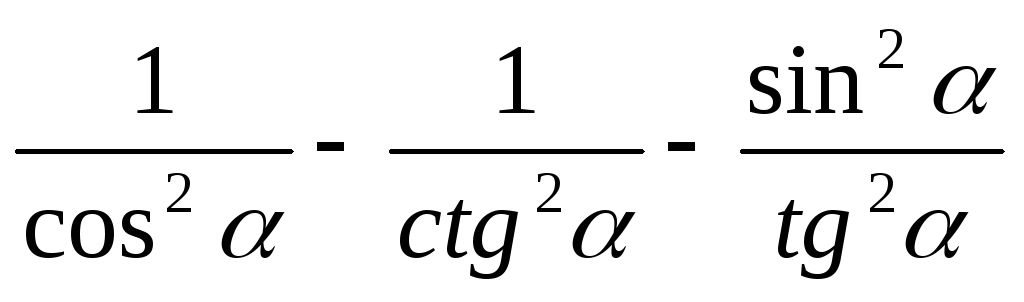 .
. -
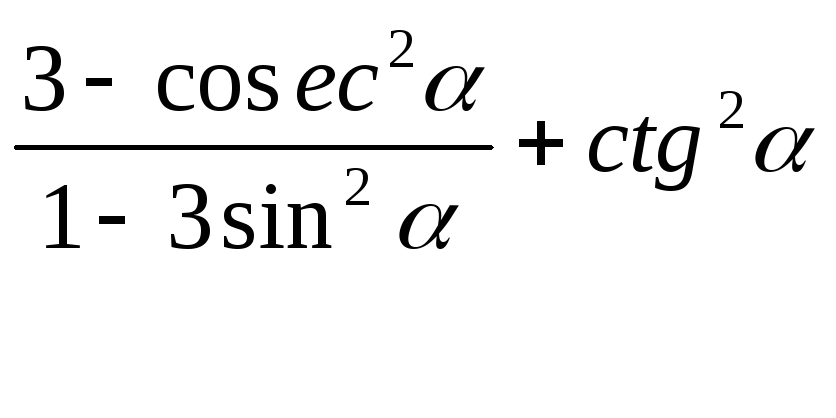 .
. -
 .
. -
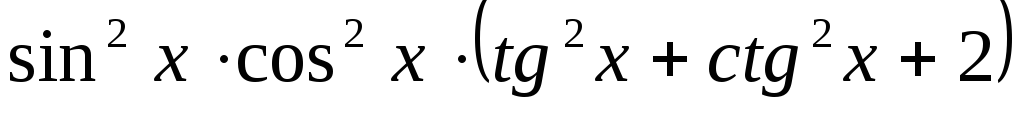 .
. -
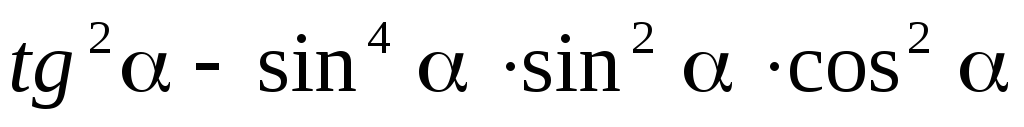 .
. -
 .
. -
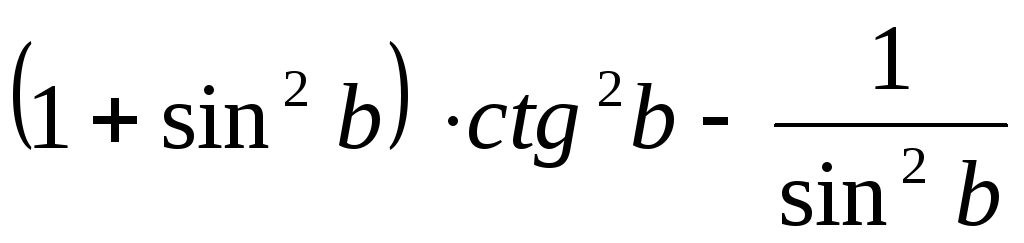 .
. -
 .
. -
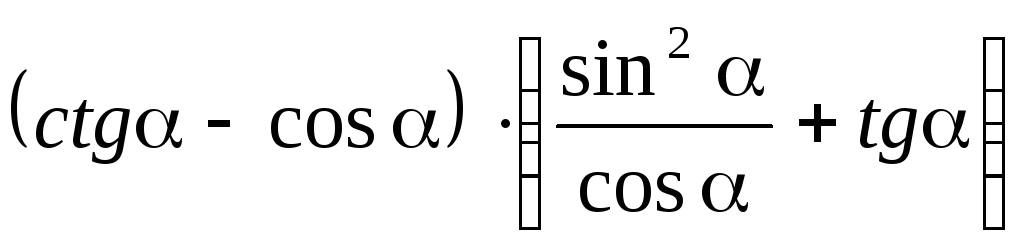 .
. -
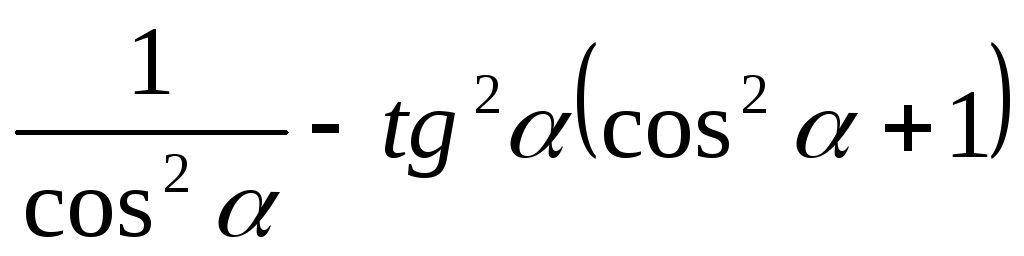 .
. -
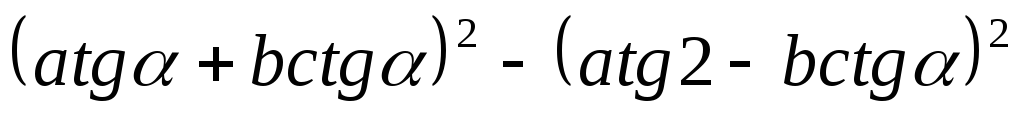 .
. -
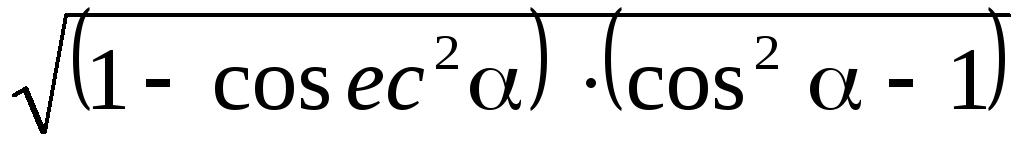 .
.
Задание 13. Доказать тождество
1.
![]() . 2.
. 2.![]() .
.
3.
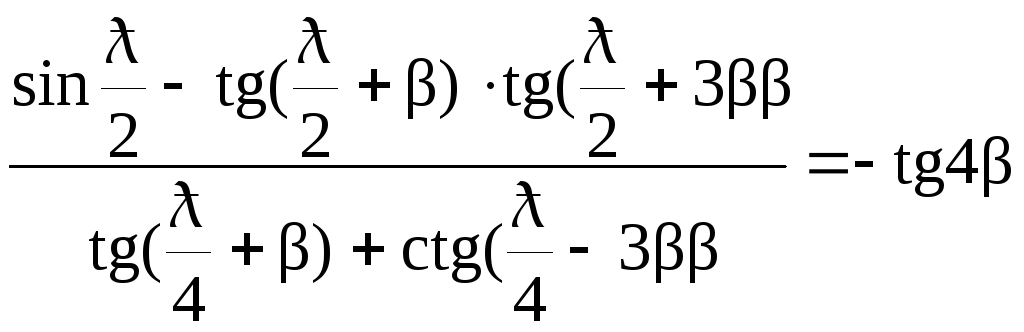 . 4.
. 4.![]() .
.
5.
![]() . 6.
. 6.![]() .
.
7.
![]() . 8.
. 8.![]() .
.
9.
![]() . 10.
. 10.![]() .
.
11. .
12.
.
12.![]()
13.
![]() .
.
-
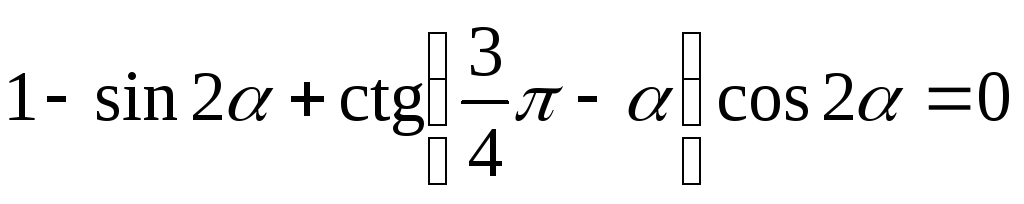
-
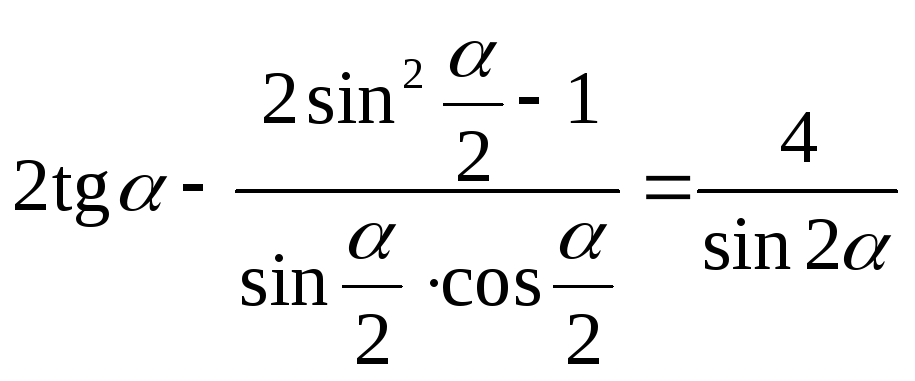
-
 .
. -
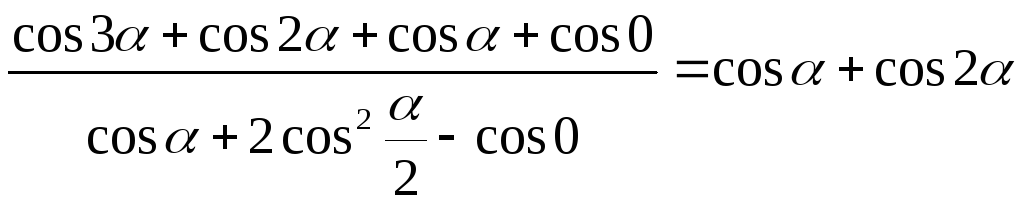 .
. -
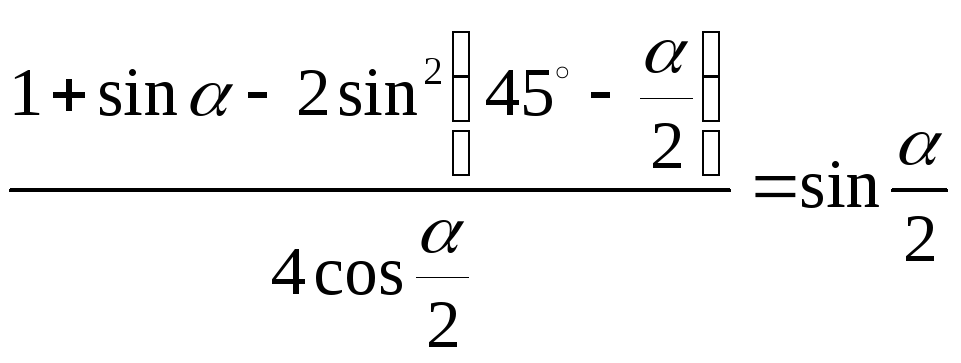 .
. -
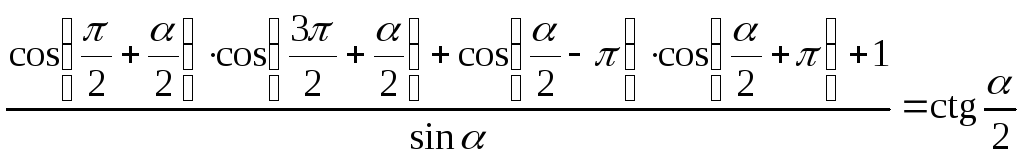 .
. -
 .
. -
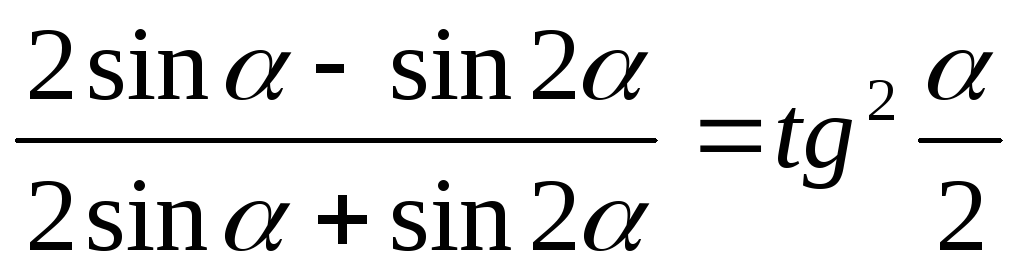 .
. -
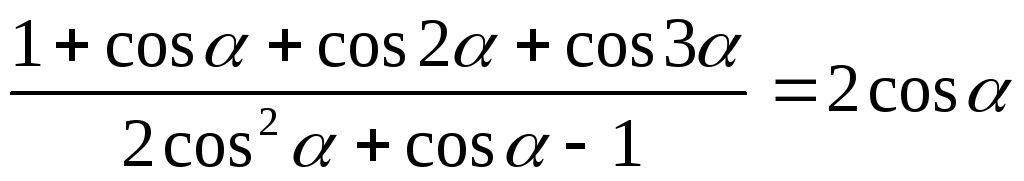 .
. -
2
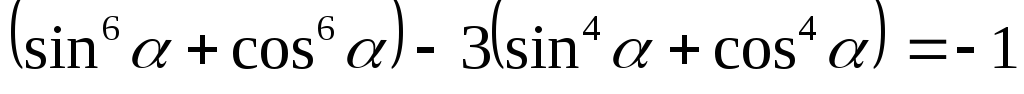 .
. -
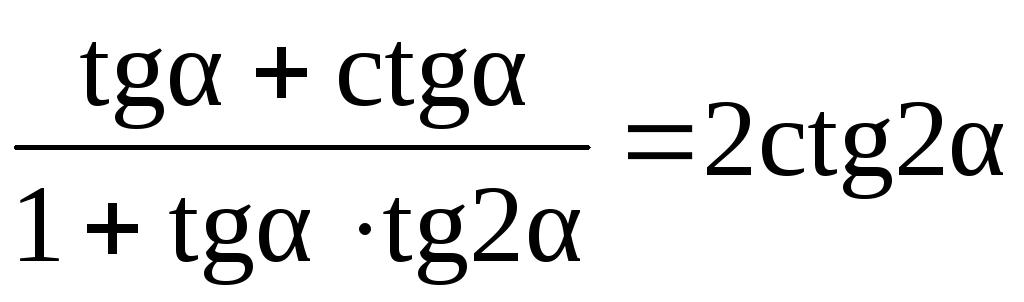 .
. -
tg
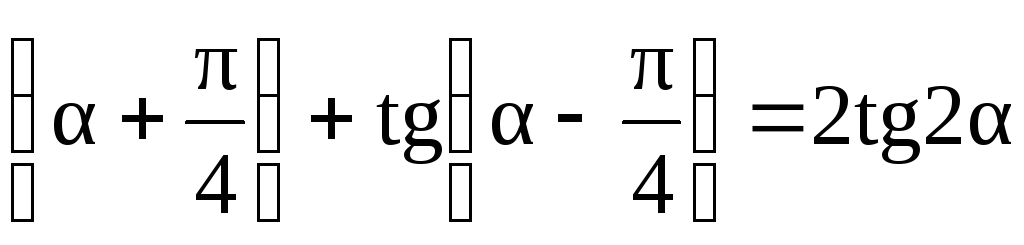 .
.
Задание 14. Решить уравнение
-
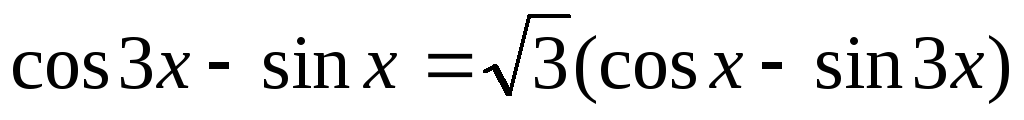 .
. -
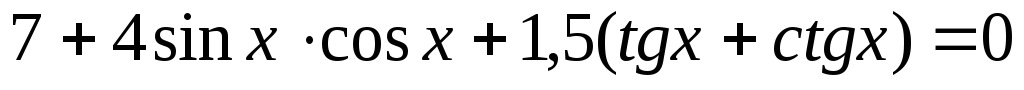 .
. -
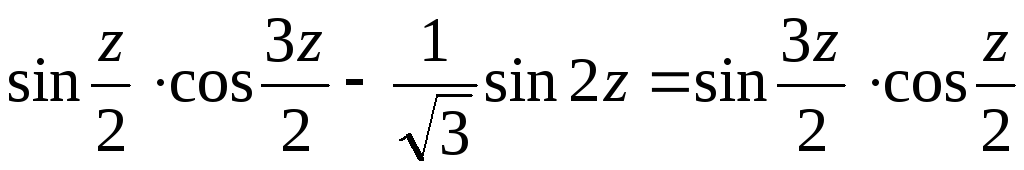 .
. -
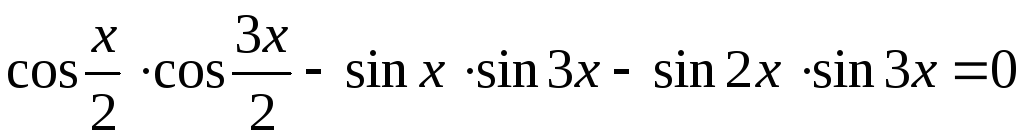 .
. -
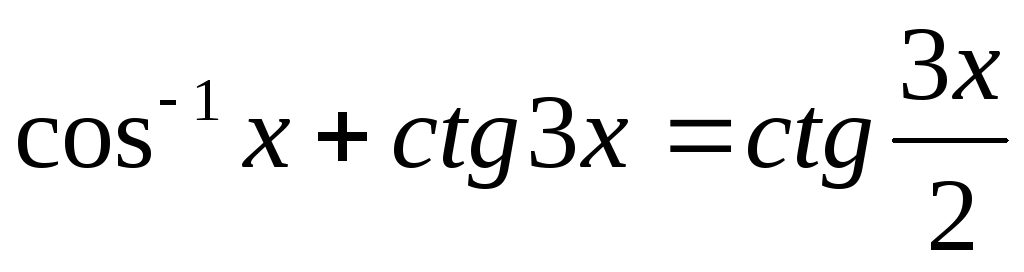 .
. -
 .
. -
 .
. -
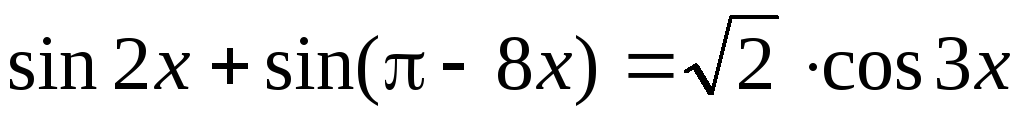 .
. -
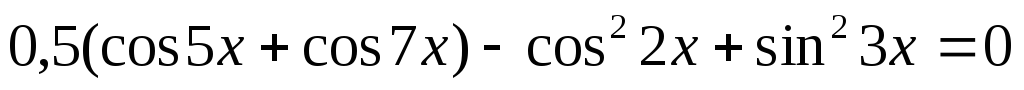 .
. -
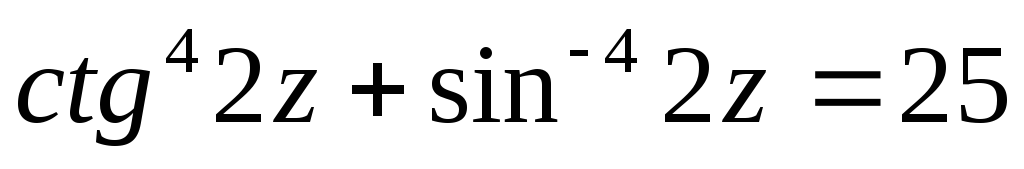 .
. -
 .
. -
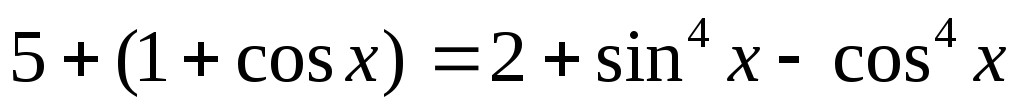 .
. -
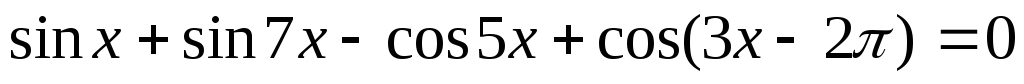 .
. -
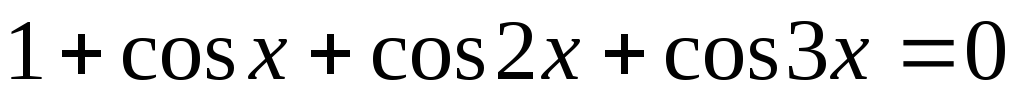 .
. -
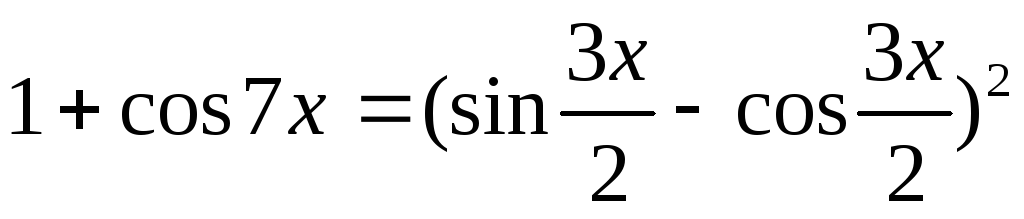 .
. -
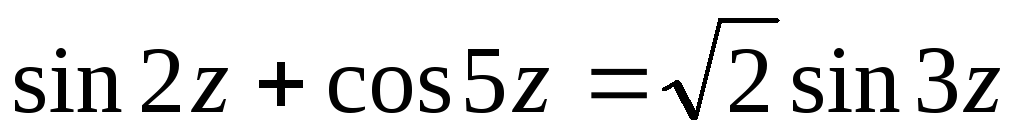 .
. -
 .
.
18.
![]() .
.
19.
![]() .
.
20.
![]() .
.
21.
![]() .
.
22.
![]() .
.
23.
![]() .
.
24.
![]() .
.
25.
![]() .
.
Задание 15. Решить уравнение
-
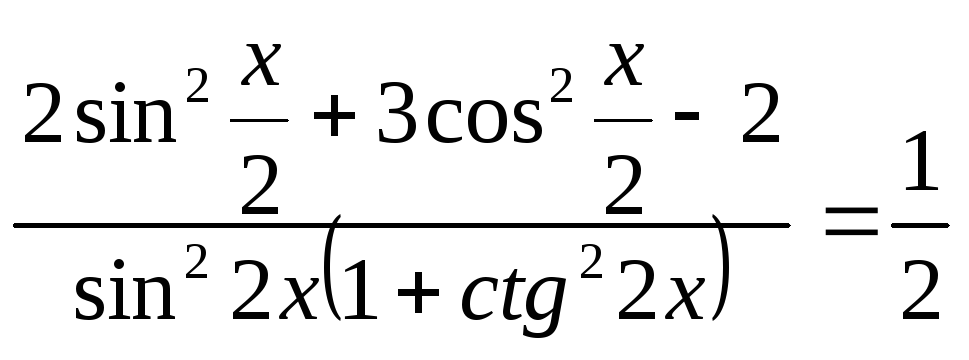 .
. -
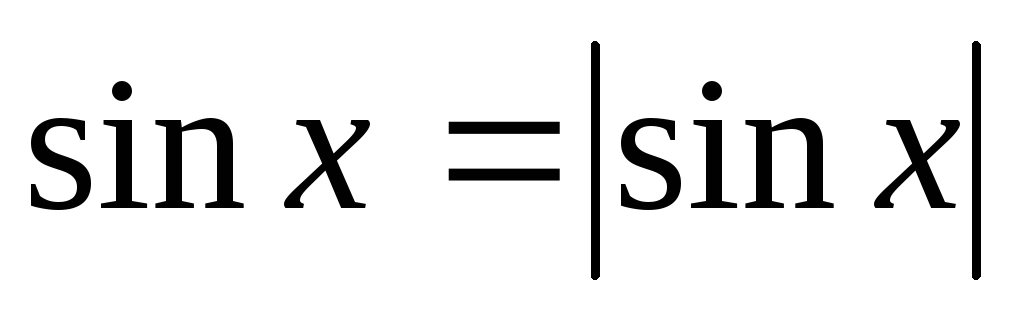 .
. -
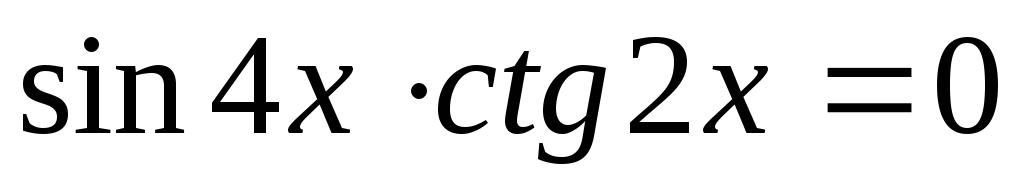 .
. -
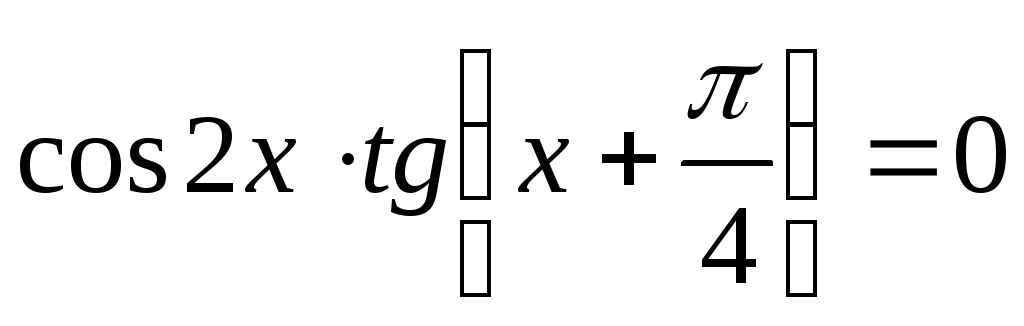 .
. -
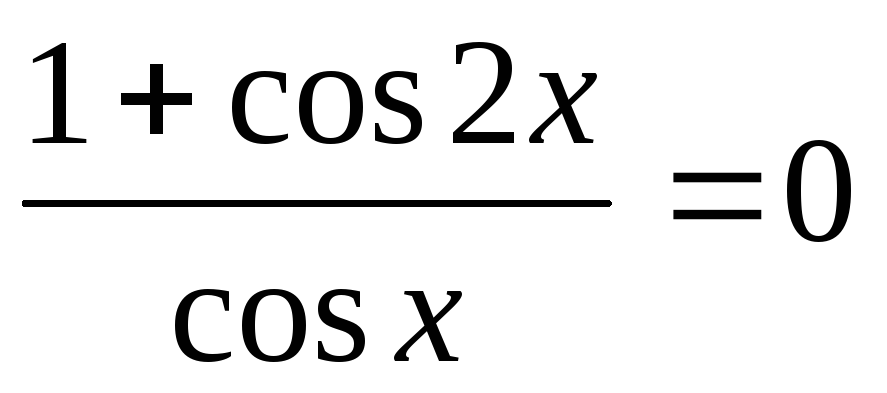 .
. -
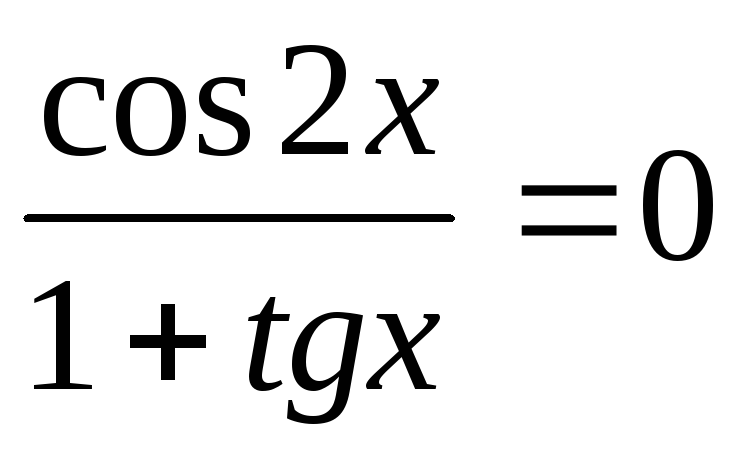 .
. -
 .
. -
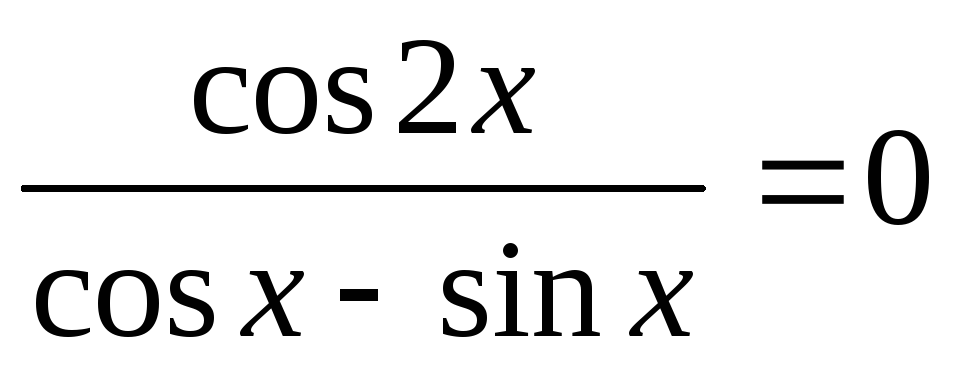 .
. -
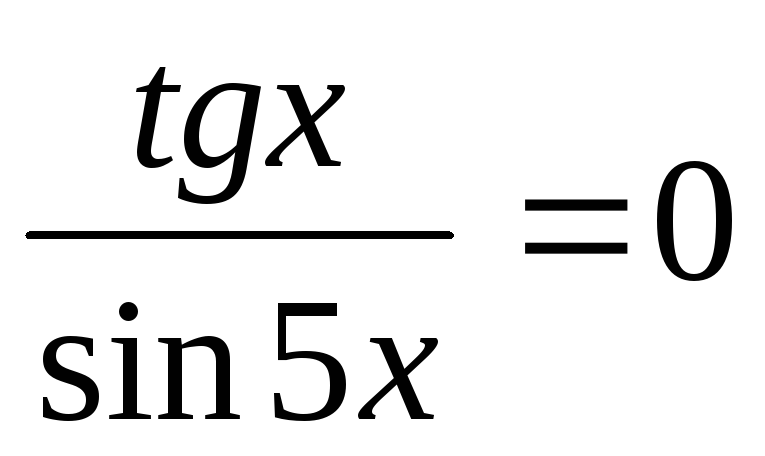 .
. -
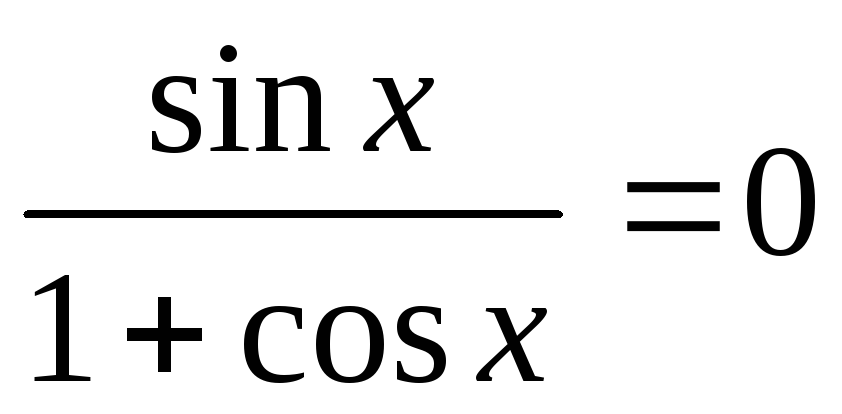 .
. -
 .
. -
 .
. -
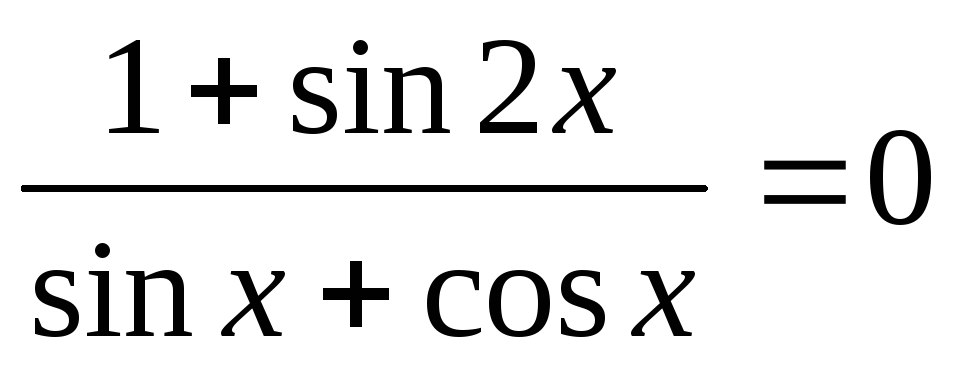 .
. -
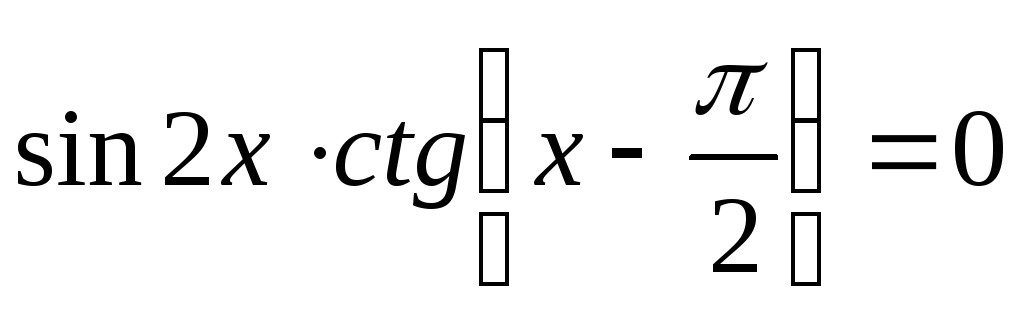 .
. -
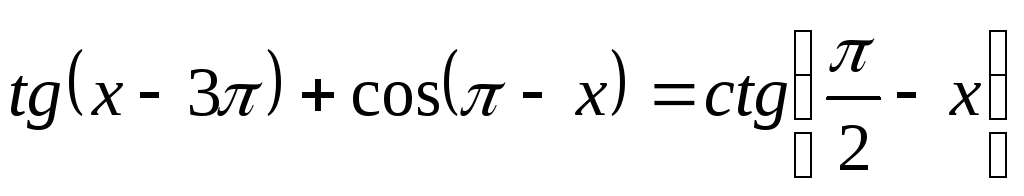 .
. -
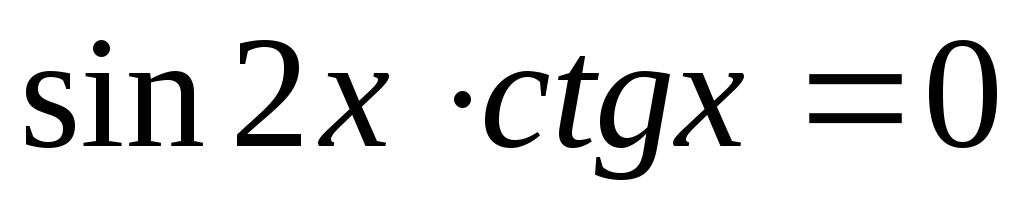 .
. -
 .
. -
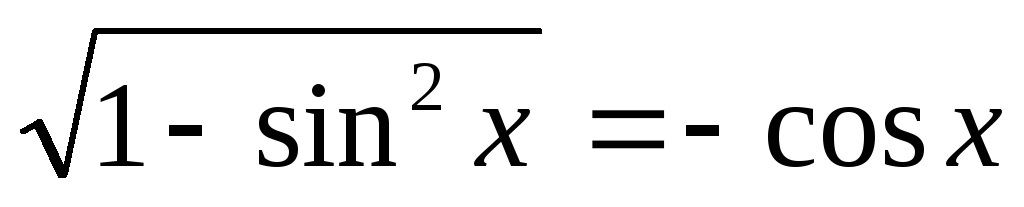 .
. -
 .
. -
 .
. -
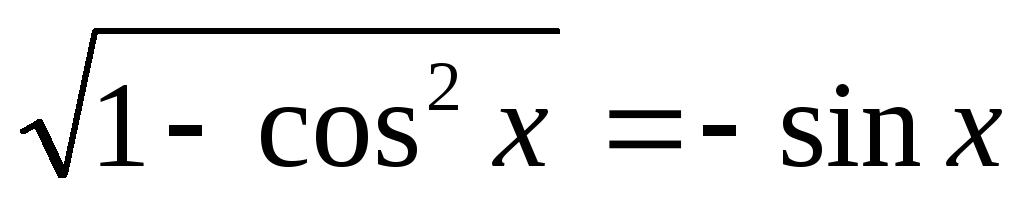 .
. -
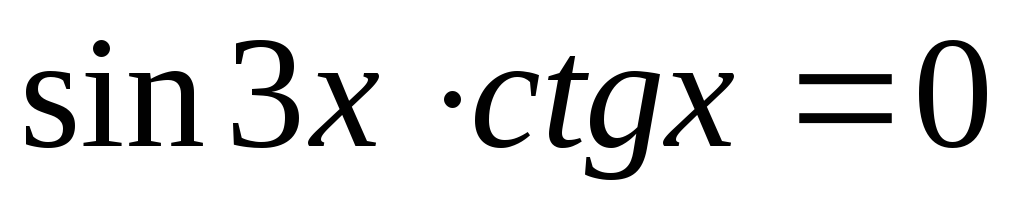 .
. -
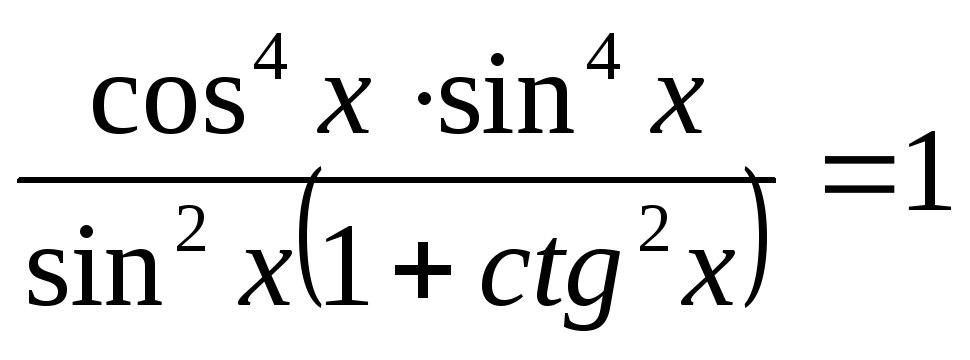 .
. -
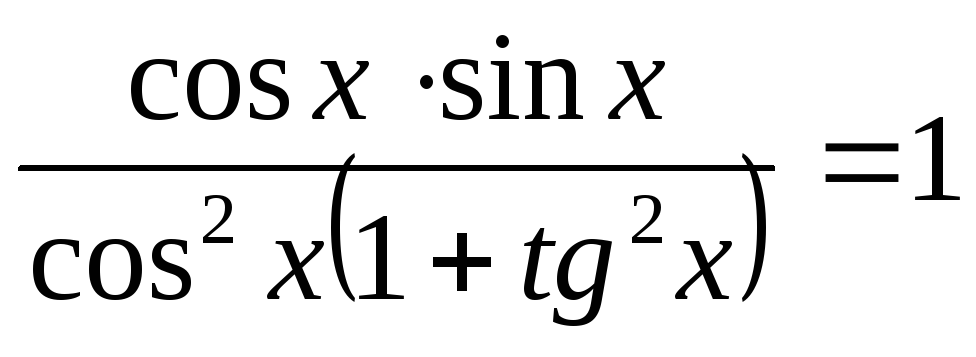 .
. -
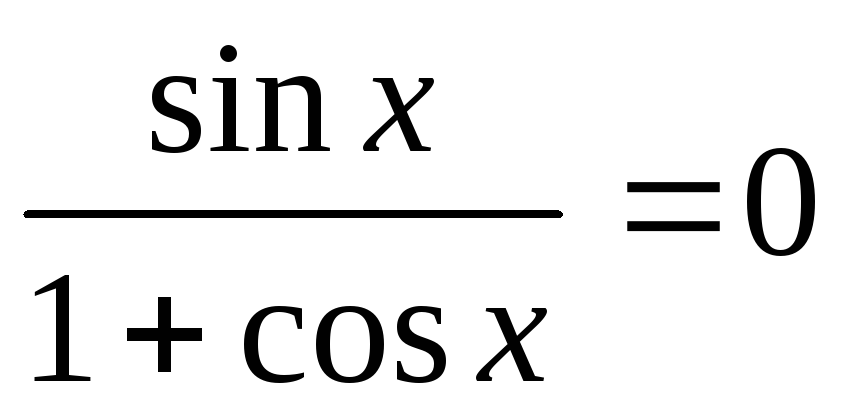 .
.
Задание 16. Решить задачу
-
В треугольнике основание равно 60 см, высота 12 см и медиана, проведенная к основанию, 13 см. Найти боковые стороны.
-
В прямоугольном треугольнике найти отношение катетов, если высота и медиана, выходящие из вершины прямого угла, относятся как 40:41.
-
В равнобедренной трапеции большее основание 44 см, боковая сторона 17 см, а диагональ 39 см. Найти площадь трапеции.
-
Площадь равнобедренной трапеции, описанной около круга, равна 8 см. Найти стороны трапеции, если угол при основании содержит 300.
-
Центр окружности, вписанной в прямоугольную трапецию, удален от концов ее боковой стороны на расстояние 3 и 9 см. Найти стороны трапеции.
-
Катеты прямоугольного треугольника 6 и 8 см. Найти расстояние от центра вписанной в треугольник окружности до центра описанной около него окружности.
-
В равнобедренный треугольник с основанием 20 см и боковой стороной 16 см вписан ромб так, что его острый угол совпадает с углом основания треугольника, а противоположная вершина лежит на боковой стороне. Вычислить сторону ромба.
-
Периметр параллелограмма равен 48 см, его высота относится как 3:5. Вычислить стороны параллелограмма.
-
Параллельные стороны трапеции 16 и 44 см, непараллельные 17 и 25 см. Найти площадь трапеции.
-
Найти отношение сторон параллелограмма, если отношение квадратов диагоналей равно 19:7 и острый угол его равен 600.
-
К окружности, вписанной в равнобедренный треугольник с основанием 12 см, проведена касательная, параллельная основанию. Найти длину отрезка касательной, заключенного между сторонами треугольника, если высота треугольника 8 см.
-
Длины оснований равнобедренной трапеции относятся как 5:12, а длина ее высоты 17 см. Найти радиус описанной около трапеции окружности, если ее средняя линия равна высоте.
-
В треугольник со сторонами 10,17 и 21 см вписан прямоугольник с периметром 24 см так, что одна его сторона лежит на большей стороне треугольника. Найти стороны прямоугольника.
-
ВД – высота треугольника АВС, точка Е – середина стороны ВС. Найти площадь круга описанного около треугольника ДВЕ, если АВ = 30 см, ВС = 26 см, АС = 28 см.
-
Определить площадь сегмента, если периметр его равен, а дуга содержит 1200.
-
Боковая сторона равнобедренного треугольника равна 10 см, основание – 12 см. К окружности, вписанной в треугольник, проведены касательные, параллельные высоте треугольника и отсекающие от него 2 прямоугольных треугольника. Найти его стороны.
-
В круг вписана трапеция, основанием которой служат диаметр и хорда, стягивающая дугу в 600. Отрезок, соединяющий середины двух непараллельных сторон трапеции, равен а. Найти площадь трапеции.
-
В прямоугольном треугольнике биссектриса острого угла делит противоположный катет на отрезок длиной 4 и 5 см. Найти площадь треугольника.
-
Найти площадь равнобедренного треугольника, если высота, опущенная на его основание, равна 10 см, а высота, опущенная на боковую сторону, равна 12 см.
-
Один из катетов прямоугольного треугольника равен 15 см, а радиус окружности, вписанной в этот треугольник, равен 3 см. Найти площадь треугольника.
-
Через концы дуги окружности, содержащей 120о, проведены касательные, и в фигуру, ограниченную этими касательными и дугой, вписана окружность. Доказать, что ее длина равна длине исходной дуги.
-
Углы треугольника равны 50о, 60о и 70о. На стороне, лежащей против угла в 50о, как на диаметре, построена окружность. На какие дуги окружность разбивается точками пересечения?
-
На сторонах AB и AD параллелограмма ABCD отложены отрезки AK=2/3 AB и AE=1/3 AD. Точки K и E соединены прямой. Найти отношение площади параллелограмма к площади треугольника.
-
Катеты в прямоугольном треугольнике относятся как 5:6, а гипотенуза равна 122 см. Найти отрезки гипотенузы, отсекаемые высотой.
-
Из внешней точки проведены к окружности секущая длиной 12 см и касательная, длина которой составляет 2/3 внутреннего отрезка секущей. Найти длину касательной.
Задание 17. Решить задачу
-
В треугольной пирамиде две боковые грани – равные равнобедренные прямоугольные треугольники. Их гипотенузы, являющиеся боковыми ребрами пирамиды, равны а и образуют между собой угол

 .
Найти объем пирамиды.
.
Найти объем пирамиды. -
В треугольной пирамиде МАВС две боковые грани АМВ и АМС перпендикулярны к плоскости основания. Ребра АС и АВ равны,
 АМВ
=
АМВ
= ,
,
 ВМС=
α. Высота пирамиды равна h.
Найти объем пирамиды.
ВМС=
α. Высота пирамиды равна h.
Найти объем пирамиды. -
найти объем и площадь боковой поверхности прямоугольного параллелепипеда, диагональ которого а составляет с плоскостью основания угол α, а с большей боковой гранью угол
 .
. -
Основанием прямой призмы служит равнобедренная трапеция, у которой боковая сторона равна меньшему основанию в, а острый угол равен
 .
Угол между диагональю призмы и диагональю
трапеции равен
.
Угол между диагональю призмы и диагональю
трапеции равен
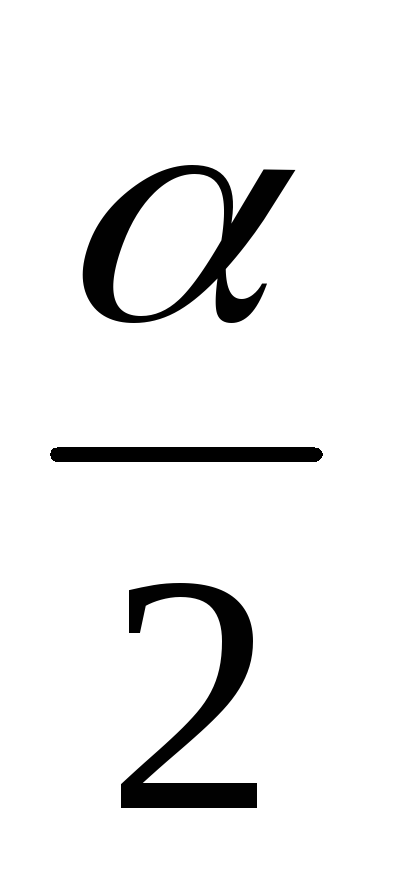 .
Найти объем призмы.
.
Найти объем призмы. -
В основании пирамиды лежит треугольник с углами α и
 .
Все боковые ребра пирамиды равны l
и наклонены к плоскости основания под
углом
.
Все боковые ребра пирамиды равны l
и наклонены к плоскости основания под
углом
 .
Найти объем пирамиды.
.
Найти объем пирамиды. -
Основанием пирамиды служит равнобедренная трапеция с боковой стороной а и острым углом
 .
Найти объем пирамиды, если каждая
боковая грань образует с основанием
угол
.
Найти объем пирамиды, если каждая
боковая грань образует с основанием
угол
 .
. -
Основанием прямой призмы является равнобедренный треугольник с площадью О и углом при вершине
 .
Плоскость. Проведенная через одну из
равных сторон основания под углом
.
Плоскость. Проведенная через одну из
равных сторон основания под углом
 к нему. Отсекает от призмы треугольную
пирамиду. Найти ее объем.
к нему. Отсекает от призмы треугольную
пирамиду. Найти ее объем. -
Высота правильной четырехугольной пирамиды h, двугранный угол при основании
 .
Найти объем и площадь полной поверхности
пирамиды.
.
Найти объем и площадь полной поверхности
пирамиды. -
основанием четырехугольной пирамиды служит ромб с острым углом
 и меньшей диагональю d.
Каждая боковая грань пирамиды наклонена
к плоскости основания под углом
и меньшей диагональю d.
Каждая боковая грань пирамиды наклонена
к плоскости основания под углом
 .
Найти площадь полной поверхности
пирамиды.
.
Найти площадь полной поверхности
пирамиды. -
В треугольной пирамиде все боковые ребра и два ребра основания равны а. Угол между равными ребрами основания равен
 .
Найти объем пирамиды.
.
Найти объем пирамиды. -
Через сторону а нижнего основания правильной призмы и середину противоположного бокового ребра поведена плоскость под углом
 к основанию. Найти объем и площадь
боковой поверхности призмы.
к основанию. Найти объем и площадь
боковой поверхности призмы. -
Основанием пирамиды служит ромб со стороной а и острым углом
 .
Две боковые грани, заключающие тупой
угол основания, перпендикулярны к
основанию, а две другие наклонены к
нему под углом
.
Две боковые грани, заключающие тупой
угол основания, перпендикулярны к
основанию, а две другие наклонены к
нему под углом
 .
Найти объем и площадь боковой поверхности
пирамиды.
.
Найти объем и площадь боковой поверхности
пирамиды. -
В основании пирамиды лежит правильный треугольник со сторонами а. Одна из боковых граней перпендикулярна к основанию, а две другие наклонены к нему под углом
 .
Найти объем и площадь боковой поверхности
пирамиды.
.
Найти объем и площадь боковой поверхности
пирамиды. -
Образующая конуса l составляет с основанием угол
 .
Найти объем описанной около пирамиды,
в основании которой лежит ромб с острым
углом
.
Найти объем описанной около пирамиды,
в основании которой лежит ромб с острым
углом
 .
. -
В правильной треугольной пирамиде стороны основания а, а плоский угол при вершине
 .
Определить объем и площадь боковой
поверхности пирамиды.
.
Определить объем и площадь боковой
поверхности пирамиды. -
В цилиндр с образующей l вписана пирамида так, что ее основание, являющееся правильным треугольником, вписано в основание цилиндра, а высота равна высоте цилиндра. Найти площадь боковой поверхности пирамиды, если две боковые грани ее перпендикулярны к основанию, а третья образует с ним угол

-
В основании пирамиды лежит ромб со стороной а и острым углом
 .
Все боковые грани наклонены к основанию
под углом
.
Все боковые грани наклонены к основанию
под углом
 .
Найти площадь полной поверхности и
объем пирамиды.
.
Найти площадь полной поверхности и
объем пирамиды. -
Основание прямой призмы служит ромб с острым углом
 .
Сечение, проведенное через большую
диагональ основания и вершину тупого
угла другого основания, является
прямоугольным треугольником с площадью
Q.
Найти объем призмы.
.
Сечение, проведенное через большую
диагональ основания и вершину тупого
угла другого основания, является
прямоугольным треугольником с площадью
Q.
Найти объем призмы. -
Основанием пирамиды служит равнобедренный треугольник с боковой стороной а и углом
 при вершине. Все боковые ребра пирамиды
составляют с высотой угол
при вершине. Все боковые ребра пирамиды
составляют с высотой угол
 .
Найти объем пирамиды.
.
Найти объем пирамиды. -
Боковое ребро правильной четырехугольной пирамиды равно m и наклонено к плоскости основания под углом
 .
Найти объем и площадь боковой поверхности
пирамиды.
.
Найти объем и площадь боковой поверхности
пирамиды. -
В правильной четырехугольной пирамиде боковое ребро l образует с высотой пирамиды угол
 .
Найти объем и площадь поверхности
пирамиды.
.
Найти объем и площадь поверхности
пирамиды. -
Высота прямоугольного параллелепипеда Н, а его диагональ составляет с основанием угол
 .
Найти объем параллелепипеда, если угол
между диагоналями его основания равен
.
Найти объем параллелепипеда, если угол
между диагоналями его основания равен
 .
. -
Основанием прямой призмы служит равнобедренный треугольник с основанием а и углом
 при вершине. Боковое ребро равно в.
Найти площадь боковой поверхности и
объем призмы.
при вершине. Боковое ребро равно в.
Найти площадь боковой поверхности и
объем призмы. -
В правильной четырехугольной пирамиде сторона основания а составляет с боковым ребром угол . Найти площадь сечения, проведенного через боковое ребро и высоту.
-
В конусе, образующая которого l наклонена к основанию под углом , вписана пирамида, в основании которой лежит прямоугольный треугольник с меньшим острым углом . Найти объем пирамиды.
