17.Граничний перехід у нерівностях для функцій Теорема про границю проміжної функції

Теорема 1(граничний перехід)

Якщо lim_x→aѓ(x)=A і lim_x→ag(x)=B і у деякому виколотому - околі точки а для х виконується нерівність ѓ(x)≤g(x)[1], тоді A≤B.

Доведення: Припустимо супротивне. Нехай АВ. Візьмемо ε=(A-B)/2. Тоді

δ₁= δ₁(ε): xУ_δ1(a)A-ε<ѓ(x)<A+ε [2], δ₂= δ₂(ε): xУ_δ2(a)B-ε<ѓ(x)<B+ε [3]. Позначимо через δ^*=min{ δ_, δ_1, δ₂}. Тоді xУ_δ*(a) будуть одночасно виконуватися нерівності [1], [2], [3]. З нерівностей [2] і [3] одержимо ѓ(x)> A-ε =A- (A-B)/2=(2A-A+B)/2=(A+B)/2=B+(A-B)/2=B+ ε>g(x). Тобто xУ_δ*(a)ѓ(x)>g(x). Але для таких х повинна виконуватись і [1]. Це неможливо. Одержана суперечність доводить теорему.

Терема 2 (про границю проміжної функції)

Якщо і у [4]. Тоді .

Доведення: за умовою тереми [5], [6]. Позначимо через Тоді будуть одночасно виконуватися нерівності [4], [5], [6]. Тобто . Звідси, . Це означає, що .

18.Перша важлива границя

Теорема [1]

Доведення: розглянемо . Функція визначена , крім . . Таким чином, парна. Звідси випливає, що у випадку існування в точці О односторонньої границі, ці границі рівні. Тобто. Нам достатньо довести, що. Побудуємо у першій чверті координатної площини ХОУ коло одиничного радіуса:. Нехай величина кута дорівнює значенню аргументу функції (х). Зрозуміло, що. , , , [2]. Поділимо всі частини [2] на : ; . Помножимо на (-1): [3]. Додамо до всіх частин нерівності [3] 1: [4]. Розглянемо: . Запишемо [4]у вигляді: [5]. Оскільки, то за теоремою про границю проміжної функції, якщо перейти у [5] до х→+0 одержимо: (оскільки ліва і права частини нерівності →0). Звідси: . Теорема доведена.

19.Друга важлива границя

Теорема [1]

Доведення: якщо . Для доведення рівності [1] покажемо спочатку, що вона виконується для , а потім - .

1)

Покажемо, що. Позначимо цілу частину х через n. Тобто . Тоді . Звідси . Або . Оскільки , то [2]. Розглянемо окремо границі n→∞ лівої і правої частин нерівності [2].Маємо. Скористаємось теоремою про границю добутку. Одержимо: . Аналогічно

. З нерівності випливає, що коли n→∞: х→+∞. Перейдемо у нерівності [2] до границі при n→∞. Оскільки ліва і права частини цієї нерівності, як було показано, прямують до ℮, то за теоремою про границю проміжної функції одержимо: .

2)

Покажемо, що. Зробимо заміну . Знайдемо х: або . Розглянемо

. Теорема доведена.

20.Нескінченно великі і нескінченно малі функції

Означення: Функція називається нескінченно великою при х→а (має границю нескінченність), якщо вона визначена в деякому околі точки а, крім, можливо, самої точки а і , М – завгодно велике, можна знайти δ=δ(М)0 таке, що х: 0|х-а|δ виконується нерівність

Геометричний зміст: яким би великим не було число M>0 всі точки графіка функцій, крім, можливо, самої точки (а, f(а)) лежать поза смугою обмеженою прямими , якщо х взято з околу (а-δ, а+δ).

О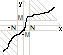значення: Функція називається нескінченно великою при х→∞ (має границю нескінченність), якщо вона визначена , де К0 деяке число і N=N(M) і таке, що N>K, що

Геометричний зміст: функція називається нескінченно великою, якщо завгодно великого знайдеться таке N>K, що як тільки х потрапляють в N- окіл нескінченно віддаленої точки значення функції будуть лежати поза смугою обмеженою прямими .

Означення: Функція називається нескінченно малою при х→а, якщо Тобто: >0

Геометричний зміст: яким би малим не було число >0 всі точки графіка функцій, крім, можливо, самої точки (а, f(а)) лежать у смузі обмеженій прямими , якщо значення х взято у околі (а-δ, а+δ).

Означення: Функція називається нескінченно малою при х→∞, якщо вона визначена , де К0 і для будь-якого завгодно малого >0 N=N()>К :

Геометричний зміст: функція при х→∞, якщо >0 знайдеться такий N- окіл нескінченно віддаленої точки для х з якого значення функції будуть лежати у смузі обмеженої прямими .

Зауваження: Аналогічно можна визначити нескінченно великі і нескінченно малі функції, якщо х→+∞ і х→-∞.