6. Граничниц перехід у нерівностях. Теор. Про границю проміжної послід.

Теорема 1 (про граничний перехід)

Якщо задані 2 послідовності {} і {} і . Якщо , , то

Доведення:

Припустимо супротивне: нехай . Розглянемо таке, що . За означенням границі для вказаної

або a -<<a + (1) також

,

або b -<<b + (2)

. Тоді одночасно виконуються нерівності (1) і (2)

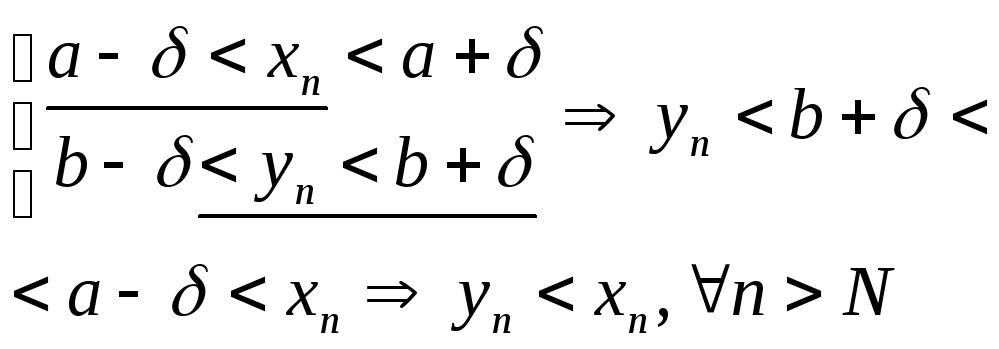
Це суперечить тому, що за умовою теореми , . Одержана суперечність доводить теорему.

Теорема 2 (про границю проміжної послідовності)

Нехай задані 3 послідовності {}, {}, {} і .Якщо , то .

Доведення:

За означенням границі (1). (2).

Позначемо через . Тоді одночасно виконуються нерівності (1) і (2). Тобто тобто . За означенням

7. Нескінченно малі послідовності

Озн. Називається нескінченно малою, якщо вона збігається до 0.

Теорема 1:

Сума скінченного числа нескінченно малих послідовностей, є нескінченно мала послідовність

Доведення

Розглянемо суму двох нескінченно малих послідовностей.

-нескінченно малі послідовності

тоді

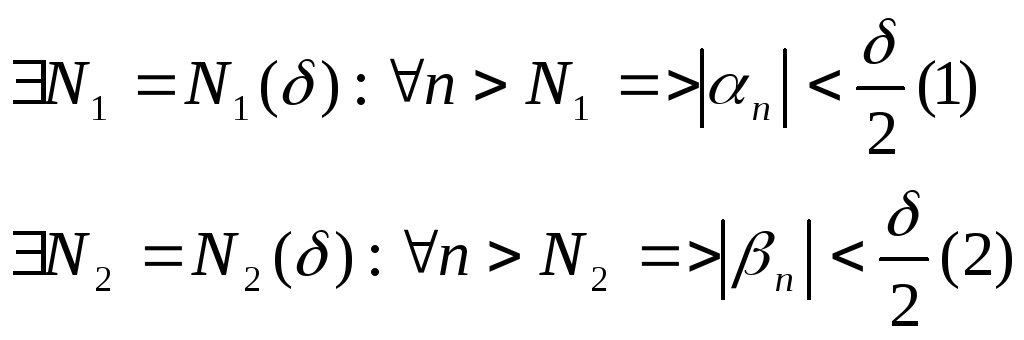
Позначимо

Тоді одночасно виконується нерівності (1) і (2)

Використовуючи властивість модуля для , маємо

Тоді

Це означає, що послідовність нескінченно мала

Теорема 2:

Добуток обмеженої послідовності на нескінченно малу послідовнічть є нескінченно мала послідовність.

Доведення

Нехай -обмежена, тоді

Якщо нескінченно мала, то -де довільне число.

Використовуючи властивість модуля,

Тобто:

Це означає, що нескінченно мала послідовність

Наслідок 1:

Добуток сталої на нескінченно малу послідовність, є нескінченно мала послідовність

Наслідок 2:

Добуток двох нескінченно малих послідовностей є нескінченно мала послідовність

Справді, якщо одну з цих послідовностей розглядати, як обмежену оскількивона має границю, то вик умови теореми 2.

Наслідок 3:

Добуток нескінченно малої послідовності на послідовність, що має границю є нескінченно мала послідовність

Теорема 3 (необхідна і достатня умова існування границі послідовності):

Для того щоб мала границю “а” необхідно і достатньо, щоб існувала нескінченно мала послідовність така, що (3)

Доведення

Необхідність

Нехай , тоді

тобто (- нескінченно мала послідовність)

Достатність

Нехай виконується рівність (3), де- нескінченно мала послідовніст, тоді за означенням

8. Нескінченно великі послідовності

Озн. Послідовність називається нескінченно великою, якщо для будь-якого завгодно великого числа M>0 натуральне число N (що залежить від M), виконується нерівність

Нескінченно велику послідовність позначають

, або .

Якщо , то пишуть

Якщо , то пишуть

Геометричний зміст нескінченно великої послідовності полягає в тому, що послідовність є нескінченновеликою, якщо у довілбному М-околі точки О інтервалу (-М;М) знаходится скінченна кількість послідовностеі, а поза ним нескінченна кількість її членів.

Зрозуміло, що нескінченно велика послідовність є не обмеженою.

Але обернене не виконується , тобто існують послідовності які не обмежені, але не є нескінченно великими.

Вказана послідовність є необмеженою, оскільки такі члени,що для будя-якого числа виконується , але не можна знайти такого N ,, тому вказана послідовність не є нескінченно великою.

=нескінченно велика послідовність

Теорема 1 (про зв'язок нескінченно малої та нескінченно великої)

Якщо , де () – нескінченно велика, то послідовність , де - нескінченно мала

Доведення

Візьмемо оскільки послідовність -нескінченно велика

Тобто

Теорема доведена

Теорема 2

Якщо послідовність , (де ) нескінченно мала , то послідовність , де - нескінченно велика.

Доведення

Доведення аналогічне попередній теоремі.