
- •1.Основні поняття матем. Логіки. Числові проміжки.
- •2.Множини
- •3.Змінні і сталі величини. Модуль величини.
- •4. Послідовність. Границя послідовності. Границя змінної.
- •5. Єдність границі послідовності. Обмежена і необмежена послідовності.
- •6. Граничниц перехід у нерівностях. Теор. Про границю проміжної послід.
- •7. Нескінченно малі послідовності
- •Необхідність
- •8. Нескінченно великі послідовності
- •9.Арефметичні операції над границями послідовностей
- •10. Монотонні послідовності
- •11.Число е
- •12.Границя за Коші. Геом. Зміст
- •13.Границя функції за Гейне
- •Достатність
- •14.Односторонні границі функції
- •Необхідність
- •15.Арефметичні операції над границями функцій
- •16.Властивість функції, що мають границю
- •17.Граничний перехід у нерівностях для функцій Теорема про границю проміжної функції
- •18.Перша важлива границя
- •19.Друга важлива границя
- •20.Нескінченно великі і нескінченно малі функції
- •21.Основні властивості нескінченно малих функцій
- •Теорема 3
- •23.Еквівалентні нескінченно малі функції
- •24.Теореми про еквівалентні нескінченно малі функції
- •25.Неперервність функції в точці
- •26.Одностороння неперервність функцій в точці. Неперервність функцій на проміжку. Точки розрива функції
- •27.Дії над неперервними функціями. Неперервність складної функції.
- •29.Деякі важливі границі:
- •31.Геометричний зміст похідної, рівняння дотичної.
- •33.Похідні суми, добутку і частки
2.Множини
Кантер
стверджував, що множина-це багато дечого,
мислимого нами як єдине. Об’єкти,що
складають множину називають її елементами.
Множини позначають велкими буквами, а
їч елементи – малими. Вираз а![]() В
означає,
що елемент а
належить множині В.
В
означає,
що елемент а
належить множині В.
Означення
Множина,
що не містить елементів, називається
порожньою. Її позначають символом
![]() .
.
Означення
Множина
А
називається підмножиною множини В,
якщо кожен елемент множини А
є елементом множини В.
Тобто
![]() х
х![]() А
А![]()
![]() В.
Це позначають А
В.
Це позначають А![]() В.
В.
Зауваження
З
означення підмножини випливає, що для
кожной множини А![]() А.
Крім того будемо вважати, що
А.
Крім того будемо вважати, що
![]() А
А
Множина натуральних чисел:
N = {1,2,3,...}
Множина цілих чисел:
Z = {…,-2,-1,0,1,2,…}
Множина раціональних чисел:
Q
=
![]() ;
m
;
m![]() Z,
n
Z,
n![]() N
N
Множина
дійсних чисел: IR
= {![]() },
де
},
де
![]() -
ціле, невід’ємне число;
-
ціле, невід’ємне число;
![]() - цифр десяткової системи числення
- цифр десяткової системи числення
N![]() Z
Z![]() Q
Q![]() IR
IR
Означення
Перетином
двох множин А
і В
називається множина С,
яка складається з елементів, що одночасно
належать і множині А
і множині В.
Перетин позначають символом
![]() .
.
С=А![]() В
В

Властивості перетину:
1.А![]() А=А
А=А
2.
А![]()
![]() =
=![]()
3.
А![]() В=В
В=В![]() А
А
4.(А![]() В)
В)
![]() С=А
С=А![]() (В
(В![]() С)
С)
5.Якщо
А![]() В,
А
В,
А![]() В=А
В=А
Означення
Множини
А
і В
називають рівними, якщо А![]() В
і А
В
і А![]() В.
Позначають А=В
В.
Позначають А=В
Означення
Об’єднанням двох множин А і В називається множина С, що складається з елементів, які належать хоча б одній з данних множин.
Позначають:
С=А![]() В
В
![]()
Властивості перетину:
1.
А![]() А=А
А=А
2.А![]()
![]() =А
=А
3.А![]() В=В
В=В![]() А
А
4.(А![]() В)
В)
![]() С=А
С=А![]() (В
(В![]() С)
С)
5.А![]() В,
то А
В,
то А![]() В=В
В=В
6.(А![]() В)
В)![]() С=(А
С=(А![]() С)
С)![]() (В
(В![]() С)
С)
7.(А![]() В)
В)![]() С=(А
С=(А![]() С)
С)![]() (В
(В![]() С)
С)
Доведення 7:
Покажемо,що
(А![]() В)
В)![]() С
С![]() (А
(А![]() С)
С)![]() (В
(В![]() С).
Нехай х
С).
Нехай х![]() (А
(А![]() В)
В)![]() С,
тоді х
С,
тоді х![]() хоча б одній з множин А
хоча б одній з множин А![]() В
або
С.
Розглянемо випадок, коли х
В
або
С.
Розглянемо випадок, коли х![]() А
А![]() В.
Тоді х
В.
Тоді х![]() А,
х
А,
х![]() В
В![]() х
х![]() А
А![]() С,
х
С,
х![]() В
В![]() С.
Звідси х
С.
Звідси х![]() (А
(А![]() С)
С)![]() (В
(В![]() С).
У випадку, коли х
С).
У випадку, коли х![]() С,
х
С,
х![]() А
А![]() С,
х
С,
х![]() В
В![]() С.
Звідси х
С.
Звідси х![]() (А
(А![]() С)
С)![]() (В
(В![]() С).
С).
Покажемо
тепер, що (А![]() С)
С)![]() (В
(В![]() С)
С)
![]() (А
(А![]() В)
В)![]() С.
Нехай х
С.
Нехай х![]() (А
(А![]() С)
С)![]() (В
(В![]() С).
Звідси х
С).
Звідси х![]() А
А![]() С
і х
С
і х![]() В
В![]() С.
Якщо х
С.
Якщо х![]() С,
то х
С,
то х![]() С
С![]() (А
(А![]() В).
Якщо х
В).
Якщо х![]() С,
то одночасно х
С,
то одночасно х![]() А,
х
А,
х![]() В.
Тому х
В.
Тому х![]() А
А![]() В
В
![]() (А
(А![]() В)
В)![]() С.
С.
Означення
Різницею множин А і В називається множина С, яка складається з елементів множини А, яких немає в множині В.
Позначення: С=А \ В
![]()
Використовуючи
позначенняалгебри множин
![]() -
окіл точки а
можна записати у вигляді:
-
окіл точки а
можна записати у вигляді:
![]() (а)={x
(а)={x![]() IR:
a
-
IR:
a
-![]() <x<a
+
<x<a
+![]() }
}
Означення
Якщо
з
![]() -
окілу точки а
виключити саму точку а,
то одержана множина називається виколотим
-
окілу точки а
виключити саму точку а,
то одержана множина називається виколотим
![]() -
околом точки а.
-
околом точки а.
Позначення:
![]() (а)
=
(а)
=![]() (а)
\
{a}
(а)
\
{a}
![]()
3.Змінні і сталі величини. Модуль величини.
Означення
Змінною називається величина, яка набуває різних числових значень. Приклад: (Температура повітря; a <x <100)
Означення
Якщо
величина набуває тільки одне значення,
її називають сталою. Приклад: (Відношення
довжини кола до його діаметра для
будь-якого кола є стала величина, що
дорівнює
![]() .
.
Знчення, що набуває змінна величина утворюють область зміни цієї величини. Ці значення мають властивість упорядкованості, тобто для будь-яких х’ і х’’ виконуєтьсяодне з трьох співвідношень:
1.х’< х’’
2.х’= х’’
3.х’> х’’
Крім того множина дійсних чисел має властивість щільності, яка полягає в тому, що між двома різними дійсними числіми знайдеться хоча б одне дійсне число.
Модуль величини.
Нагадаємо означення модуля:
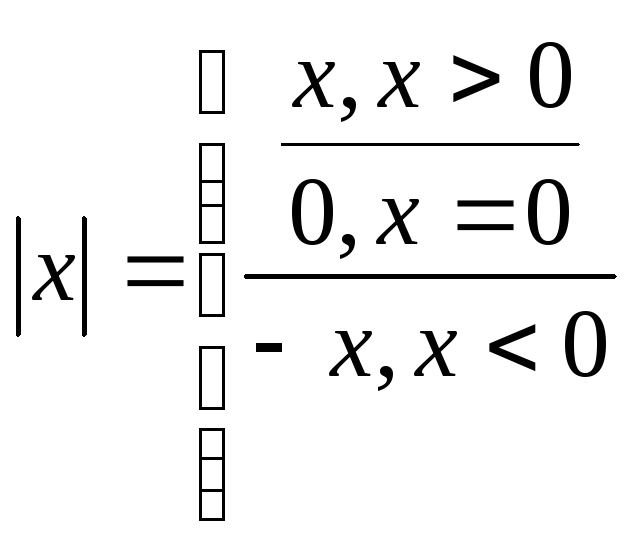
Геометрично модуль лійсного числа дорівнює відстані від точки, що зображує данне число на числовій осі до початку координат.
Властивості:
1.![]()
![]() 0
0
2.![]()
![]() 0
0
3.![]()
4.![]()
5.![]()
6.![]()
7.![]()
8.![]()
Доведення
6:
![]()
1.![]()
2.![]()
