
- •Глава 1. Алгебра логики
- •1.1. Функции алгебры логики
- •1.2. Элементарные булевы функции
- •1.3. Формульное представление булевой функции
- •1.4. Существенные и фиктивные переменные
- •1.5. Эквивалентные соотношения (тождества) алгебры логики
- •1.6. Разложение булевой функции по подмножеству переменных и совершенные нормальные формы
- •1.7. Двойственная функция
- •1.8. Полнота систем булевых функций
- •1.9. Функции k-значной логики
- •1.10. Контрольные вопросы к главе 1
1.5. Эквивалентные соотношения (тождества) алгебры логики
Приведем список тождеств, характеризующих свойства элементарных функций. Использование этих тождеств полезно при решении задач.
Свойство ассоциативности:
1. ((![]()
![]() )
)![]() )=(
)=(![]() (
(![]()
![]() ))
=
))
=
![]()
![]()
![]() ,
где
– только одна из функции {,
,
}.
,
где
– только одна из функции {,
,
}.
Свойство коммутативности:
2. (![]()
![]() )=(
)=(![]()
![]() ).
).
Дистрибутивные законы:
3. (![]()
![]() )&
)&![]() =(
=(![]() &
&![]() )(
)(![]() &
&![]() ).
).
4. (![]() &
&![]() )
)![]() =(
=(![]()
![]() )&(
)&(![]()
![]() ).
).
5. (![]()
![]() )&
)&![]() =(
=(![]() &
&![]() )
(
)
(![]() &
&![]() ).
).
Правила Де Моргана:
6. (![]() )=
)=![]() &
&![]() .
.
7. (![]() )=
)=![]()
![]() .
.
8.
![]() =
=![]() .
.
Свойства 0 и 1:
9.
![]()
1 =
1.
1 =
1.
10.
![]()
0
=
0
=![]() .
.
11.
![]() &
1
=
&
1
=![]() .
.
12.
![]() &
0 =
0.
&
0 =
0.
Закон противоречия:
13.
![]() &
&![]() =
0.
=
0.
Закон исключения третьего:
14.
![]()
![]() =
1.
=
1.
Законы идемпотентности:
15.
![]()
![]() =
=![]() .
.
16.
![]() &
&![]() =
=![]() .
.
Закон поглощения:
17.
![]() &
&![]()
![]() =
=![]() (или
(или
![]()
![]()
![]() =
=![]() ).
).
Правило простого склеивания:
18.
![]()
![]()
![]()
![]() =
=![]() .
.
Обобщенное склеивание:
19.
![]()
![]()
![]()
![]() =
=![]()
![]()
![]()
![]()
![]()
![]() .
.
Еще несколько дополнительных правил:
20.
![]()
![]() =
=![]()
![]() .
.
21.
![]()
![]() =
=![]()
![]()
![]()
![]() .
.
22.
![]() ~
~![]() =
=![]()
![]()
![]()
![]() .
.
23.
![]() /
/![]() =
=![]() =
=![]()
![]() .
.
24.
![]()
![]() =
=![]() =
=![]()
![]() .
.
Утверждение.
Если
![]() – подформула формулы B,
то при замене ее вхождения на эквивалентную
подформулу
– подформула формулы B,
то при замене ее вхождения на эквивалентную
подформулу
![]() формула B
перейдет в формулу A,
эквивалентную B.
формула B
перейдет в формулу A,
эквивалентную B.
Этот принцип вместе с эквивалентными соотношениями позволяет осуществлять эквивалентные преобразования и получать новые эквивалентные соотношения.
Пример. Используя основные эквивалентности, проверим равенство x (y z) = (x y) (x z).
На основании
тождества (20) получим
![]() (
(![]()
z)
=
z)
=
![]()
(
(![]()
z).
Применим один из законов Де Моргана и
тождество (8), опустим лишние скобки
(тождество (1)) и получим
z).
Применим один из законов Де Моргана и
тождество (8), опустим лишние скобки
(тождество (1)) и получим
![]()
![]()
z
=
z
=
![]()
![]()
z.
Далее применяем правила обобщенного
склеивания к подформуле
z.
Далее применяем правила обобщенного
склеивания к подформуле
![]()
![]() ,
преобразуем соотношение к виду
,
преобразуем соотношение к виду
![]()
![]()
z
=
z
=
![]()
![]()
![]()
z.
Выполняем поглощение произведения
z.
Выполняем поглощение произведения
![]() сомножителем
сомножителем
![]() ,
в результате получаем окончательное
соотношение
,
в результате получаем окончательное
соотношение
![]()
![]()
z
=
z
=
![]()
![]()
z.
z.
КАДР
1.6. Разложение булевой функции по подмножеству переменных и совершенные нормальные формы
Введем обозначение
![]() ,
где {0,
1}. Очевидно
,
где {0,
1}. Очевидно
![]()
Заметим, что
![]() =
1 тогда и только тогда, когда x
= .
=
1 тогда и только тогда, когда x
= .
![]() – любое произведение
из m
переменных. Число всевозможных
произведений есть
– любое произведение
из m
переменных. Число всевозможных
произведений есть
![]() .
.
![]() – функция f
с фиксацией m
первых переменных некоторыми константами.
– функция f
с фиксацией m
первых переменных некоторыми константами.
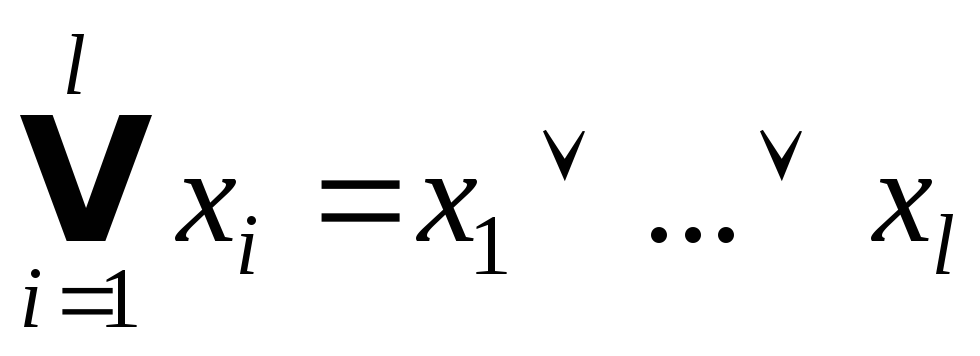 .
.
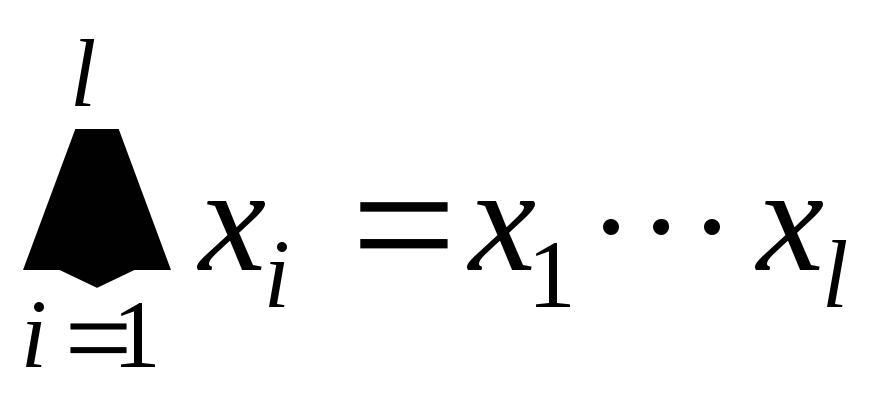 .
.
Теорема 1.1.
Любая булева функция
![]() может быть разложена по m
переменным,
может быть разложена по m
переменным,
![]() ,
следующим образом:
,
следующим образом:
![]() . (1)
. (1)
Доказательство.
Рассмотрим произвольный набор
![]() значений переменных
значений переменных
![]() ,
подставим его в левую и правую части
нашего равенства, покажем, что левая и
правая части соотношения (1) принимают
одно и то же значение.
,
подставим его в левую и правую части
нашего равенства, покажем, что левая и
правая части соотношения (1) принимают
одно и то же значение.
Левая часть имеет
вид
![]() .
.
Правая часть имеет
вид![]() .
Если
.
Если
![]() и
и
![]() – различны, то
– различны, то
![]() = 0 и из
= 0 и из
![]() слагаемых остается только одно
слагаемых остается только одно
![]() ,
так как
,
так как
![]() =1,
то
=1,
то
правая часть =
![]() = левая часть.
= левая часть.
Ч.Т.Д.
Частные случаи (1.1):
1) разложение по одной переменной:
![]() .
Такое разложение называется разложением
(декомпозицией) Шеннона;
.
Такое разложение называется разложением
(декомпозицией) Шеннона;
2) разложение по всем переменным:
![]() .
Если
.
Если
![]() =
0, то логическое произведение
=
0, то логическое произведение
![]() удаляется. В результате имеем
удаляется. В результате имеем
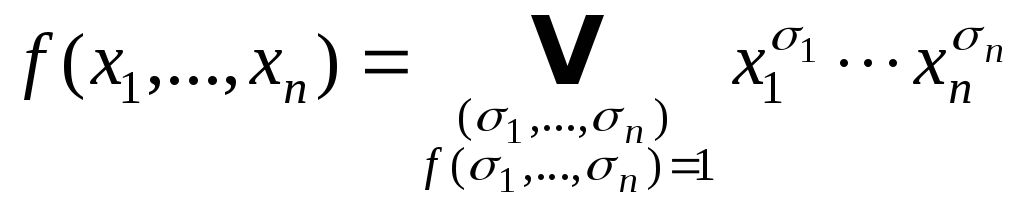 .
Такое разложение называется совершенной
дизъюнктивной нормальной формой
(Сов.ДНФ).
.
Такое разложение называется совершенной
дизъюнктивной нормальной формой
(Сов.ДНФ).
КАДР
Алгоритм построения Сов.ДНФ по таблице истинности.
1. Строим таблицу истинности булевой функции.
2. В векторе-столбце значений функции выбираем очередную единицу. Если единицы исчерпаны, то идем в п. 4.
3. По набору значений переменных выбранной строки формируем конъюнкцию всех аргументов с соблюдением следующего правила: если i-я компонента набора равна 0, то i-я переменная входит в конъюнкцию с инверсией, иначе – без инверсии. Полученную конъюнкцию добавляем в формулу как очередное слагаемое. Идем в п. 2.
4. Конец алгоритма.
Пример. Применим алгоритм к функции, заданной таблицей истинности (табл. 1.8).
|
Таблица 1.8 |
|
|||
|
|
|
|
f
( |
|
|
0 |
0 |
0 |
1 |
|
|
0 |
0 |
1 |
1 |
|
|
0 |
1 |
0 |
0 |
|
|
0 |
1 |
1 |
1 |
|
|
1 |
0 |
0 |
0 |
|
|
1 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
1 |
|
|
1 |
1 |
1 |
1 |
|
Соединив полученные конъюнкции знаком дизъюнкции, имеем
![]()
![]()
![]()
![]()
![]()
![]() .
.
Теорема 1.2.
Любая булева функция может быть
представлена формулой над множеством
элементарных функций {,
,
![]() }.
}.
Доказательство.
1) Пусть
![]() = 0, тогда
= 0, тогда
![]() =
=
![]() ,
i
{1,…, n}.
,
i
{1,…, n}.
2) Пусть
![]()
0, тогда
0, тогда
 .
.
Ч.Т.Д.
Сов.ДНФ булевой функции единственна. Такое представление булевых функций может быть использовано для сравнения.
Применим разложение
(1) для
![]() :
:
![]() .
.
Возьмем инверсию правой и левой частей нашего равенства:
![]() =
=
=![]() =
=
![]() .
.
Если
![]() = 1, то вся скобка в логическом произведении
превращается в константу 1. В итоге имеем
= 1, то вся скобка в логическом произведении
превращается в константу 1. В итоге имеем
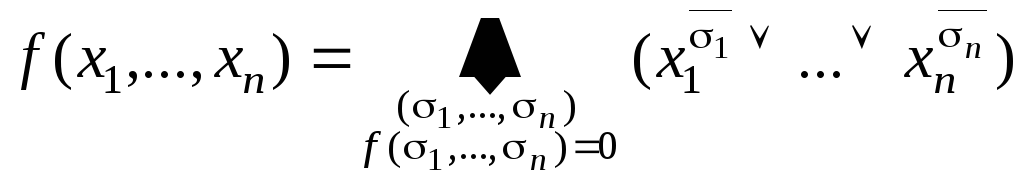 – совершенная
конъюнктивная нормальная форма (Сов.КНФ).
– совершенная
конъюнктивная нормальная форма (Сов.КНФ).
КАДР
Алгоритм построения Сов.КНФ по таблице истинности.
1. Строим таблицу истинности булевой функции.
2. В векторе-столбце значений функции выбираем очередной 0. Если нули исчерпаны, то идем в п. 4.
3. По набору значений переменных выбранной строки формируем дизъюнкцию всех аргументов с соблюдением следующего правила: если i-я компонента набора равна 0, то i-я переменная входит в дизъюнкцию без инверсии, иначе – с инверсией. Полученную дизъюнкцию добавляем в формулу как очередной сомножитель. Идем в п. 2.
4. Конец алгоритма.
Пример. Применим алгоритм к функции, заданной таблицей истинности (табл. 1.9).
|
Таблица 1.9 |
|
|||
|
|
|
|
f
( |
|
|
0 |
0 |
0 |
1 |
|
|
0 |
0 |
1 |
1 |
|
|
0 |
1 |
0 |
0 |
|
|
0 |
1 |
1 |
1 |
|
|
1 |
0 |
0 |
0 |
|
|
1 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
1 |
|
|
1 |
1 |
1 |
1 |
|
Соединив полученные дизъюнкции знаком конъюнкции, имеем
(![]() )
(
)
(![]() ).
).
КАДР
