Доверительный интервал для среднеквадратического отклонения .

Пусть неизвестны. Можно показать, что тогда случайная величина имеет распределение с (n – 1) степенями свободы. По доверительной вероятности определяют , по таблице квантилей распределения с n – 1 степенями свободы определяют квантили уровней и 1 - : , . Имеет место соотношение

. Строим доверительный интервал для среднеквадратического отклонения

.

Объяснение причин, по которым параметры распределены по Стъюденту или , требуют более глубокого рассмотрения материала. Но для догадки можно использовать два известных результата:

• если x_{1, …}x_n распределены нормально, то имеет распределение с n степенями свободы

• если x распределена нормально, а y по с n степенями свободы, то случайная величина 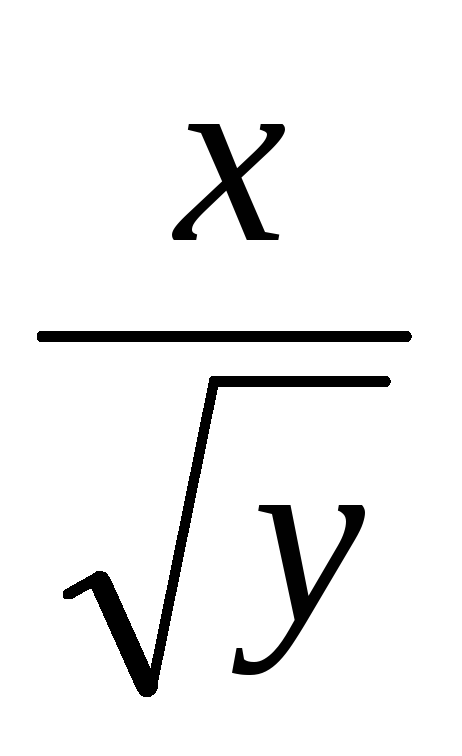распределена по Стъюденту.

Содержание

Лекция 1 Вероятность 2

Лекция 2 Условная вероятность 9

Лекция 3 Случайные величины 14

Лекция 4 Повторные испытания 18

Лекция 5 Экспоненциальное и нормальное распределения 21

Лекция 6 Двумерные случайные величины 24

Лекция 7 Законы больших чисел и центральная предельная теорема 29

Лекция 8 Элементы математической статистики 34

1 Лекции 1,2 написаны по лекциям В.Ф. Панова с добавлением авторского материала и примеров