
- •Экономико-математические методы и модели: оптимизационные методы и модели
- •1. Введение
- •2. Общая задача математического программирования. Формы записи задач линейного программирования
- •3. Составление математических моделей простейших экономических задач
- •3. Задание целевой функции.
- •3. Задание целевой функции.
- •4. Графический метод решения задачи линейного программирования
- •4.1. Геометрическая интерпретация задачи линейного программирования
- •4.2. Алгоритм графического решения задачи линейного программирования
- •5. Симплексный метод решения задач линейного программирования
- •Построение математической модели экономической задачи.
- •3. Задание целевой функции.
- •2. Построение начального опорного плана.
- •3. Построение первоначальной симплекс-таблицы.
- •4. Вычисление оценок (значений критерия оптимальности плана).
- •Критерий оптимальности опорного плана
- •Критерий единственности опорного плана
- •5. Симплекс-критерии перехода к новому опорному плану.
- •Симплекс-критерий I включения вектора в базис
- •Симплекс-критерий II исключения вектора из базиса
- •6. Алгоритм перехода к новому базису.
- •6. Алгоритм решения задачи симплексным методом
- •6. Метод искусственного базиса
- •Особенности метода искусственного базиса
- •7. Транспортная задача (тз) линейного программирования
- •7.1. Постановка и математическая модель транспортной задачи
- •7.2. Алгоритм решения транспортной задачи
- •7.3. Опорный план транспортной задачи
- •7.3.1. Метод вычеркивания проверки опорности плана (образования цикла)
- •7.4. Построение начального опорного плана транспортной задачи
- •7.4.1. Метод северо-западного угла
- •7.4.2. Метод минимальной стоимости
- •Запишем математическую модель поставленной задачи.
- •2. Построение начального опорного плана методом минимальной стоимости.
- •Метод потенциалов.
- •Вычисление потенциалов
- •Проверка оптимальности плана
- •Переход от одного опорного плана к другому
4. Вычисление оценок (значений критерия оптимальности плана).
После заполнения указанных столбцов
симплекс-таблицы необходимо определить,
является ли начальный опорный план
![]() оптимальным.
оптимальным.
Критерий оптимальности опорного плана
Опорный план
![]() задачи линейного программирования
является оптимальным
задачи линейного программирования
является оптимальным
![]() ,
если для всех векторов
,
если для всех векторов
![]() системы ограничений выполняется условие
системы ограничений выполняется условие
![]() (для задачи максимизации),
(26)
(для задачи максимизации),
(26)
или
![]() (для задачи минимизации),
(27)
(для задачи минимизации),
(27)
![]() .
(28)
.
(28)
Если хотя бы для одного из векторов
![]() критерий оптимальности (26) или
(27) не выполняется, то опорный
план
критерий оптимальности (26) или
(27) не выполняется, то опорный
план
![]() не является оптимальным.
не является оптимальным.
Здесь
![]() - число, равное значению целевой функции,
если в качестве переменных подставить
значения коэффициентов разложения
- число, равное значению целевой функции,
если в качестве переменных подставить
значения коэффициентов разложения
![]() вектора
вектора
![]() по векторам базиса;
по векторам базиса;
![]() - оценка разложения вектора
- оценка разложения вектора
![]() по векторам базиса. Для ее вычисления
необходимо из скалярного произведения
векторов-столбцов
по векторам базиса. Для ее вычисления
необходимо из скалярного произведения
векторов-столбцов
![]() и
и
![]() вычесть соответствующий коэффициент
вычесть соответствующий коэффициент
![]() целевой функции.
целевой функции.
Критерий единственности опорного плана
Оптимальный план
![]() является единственным,
если для любого вектора условий
является единственным,
если для любого вектора условий![]() ,
не входящего в базис
,
не входящего в базис
![]() ,
оценка
,
оценка
![]() не равна нулю:
не равна нулю:
![]() ,
для
,
для
![]() .
(29)
.
(29)
В противном случае задача имеет альтернативные оптимальные планы.
В последнюю строку «Оценка»
симплекс-таблицы в столбцах
![]() заносят результаты вычисления
оценок для каждого из векторов
заносят результаты вычисления
оценок для каждого из векторов
![]() :
:
![]()
![]()
![]()
![]()
![]()
![]() .
.
В столбце «План
![]() »
оценочного ряда заносится значение
целевой функции
»
оценочного ряда заносится значение
целевой функции
![]() для начального плана
для начального плана
![]()
![]() .
.
Так как оценки
![]() и
и
![]() отрицательны, то план
отрицательны, то план
![]() не является оптимальным и необходимо
перейти к другому опорному плану.
не является оптимальным и необходимо
перейти к другому опорному плану.
5. Симплекс-критерии перехода к новому опорному плану.
Переход к новому опорному плану
осуществляется путем замены базиса и
перехода к новым базисным переменным.
Из текущего базиса
![]() необходимо исключить один из базисных
векторов
необходимо исключить один из базисных
векторов
![]() или
или
![]() (одну из базисных переменных
(одну из базисных переменных
![]() или
или
![]() )
и включить вместо него один из небазисных
векторов
)
и включить вместо него один из небазисных
векторов
![]() или
или
![]() и соответствующую свободную переменную.
Получим новый базис
и соответствующую свободную переменную.
Получим новый базис
![]() с соответствующими новыми базисными
переменными.
с соответствующими новыми базисными
переменными.
Симплекс-критерий I включения вектора в базис
Если для задачи максимизации
в строке оценок есть отрицательные
оценки
![]() (для задачи минимизации - положительные
оценки
(для задачи минимизации - положительные
оценки
![]() ),
соответствующие небазисным переменным,
то в новый базис войдет вектор условий
),
соответствующие небазисным переменным,
то в новый базис войдет вектор условий![]() с номером
с номером
![]() ,
соответствующий максимальной по
абсолютной величине отрицательной
(положительной) оценке
,
соответствующий максимальной по
абсолютной величине отрицательной
(положительной) оценке
![]() для
для
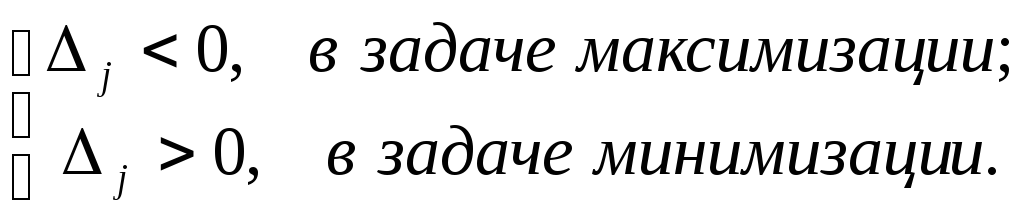 (30)
(30)
Если таких максимальных оценок
![]() несколько, то в базис вводится вектор,
соответствующий максимальному
коэффициенту
несколько, то в базис вводится вектор,
соответствующий максимальному
коэффициенту
![]() целевой функци.
целевой функци.
Направляющим столбцом
называется столбец симплекс-таблицы
(столбец матрицы ограничений с номером
![]() ),
в котором находится включаемый в базис
вектор
),
в котором находится включаемый в базис
вектор
![]() .
.
Если в направляющем столбце симплекс-таблицы нет положительных элементов
![]() ,
(31)
,
(31)
то целевая функция неограниченна и оптимальный план не существует.
В новом базисе целевая функция получит максимально возможное положительное (отрицательное) приращение и приблизится к максимальному (минимальному) оптимальному значению.
В рассматриваемой задаче максимизации
отрицательными являются оценки
![]() и
и
![]() .
Максимальная по абсолютной величине
оценка
.
Максимальная по абсолютной величине
оценка
![]() равна
равна
![]() и находится во втором столбце
и находится во втором столбце
![]() .
Поэтому в новый базис будет включен
вектор
.
Поэтому в новый базис будет включен
вектор
![]() ,
соответствующий новой базисной переменной
,
соответствующий новой базисной переменной
![]() .
Направляющий второй столбец выделен
цветом в симплекс-таблице.
.
Направляющий второй столбец выделен
цветом в симплекс-таблице.
Для определения базисного вектора и переменной, которые необходимо исключить из текущего базиса, используется второй симплекс-критерий, обеспечивающий неотрицательность правых частей системы уравнений ограничений.
