Построение математической модели экономической задачи.

1. Выбор переменных. Переменными задачи являются объемы производства каждого вида продукции, то есть, план производства.

2. Система ограничений. Суммарное время работы каждого из станков, которое равно сумме произведений времени обработки соответствующей единицы продукции на объем ее производства , не должно превышать установленного лимита. Объемы производства должны быть неотрицательными. Система ограничений имеет вид:

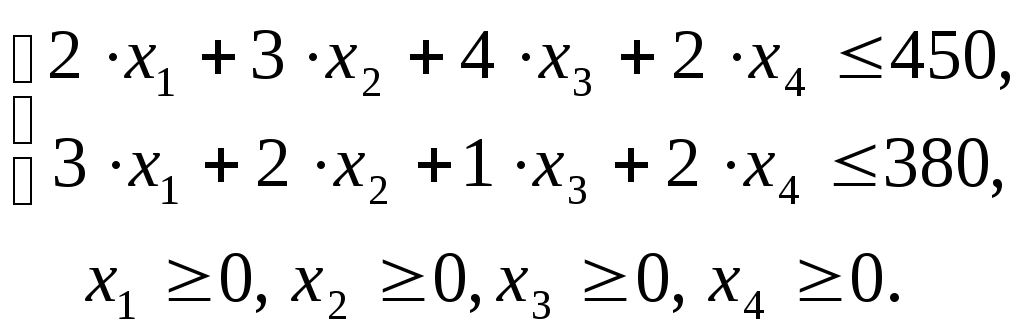
3. Задание целевой функции.

Критерием оптимизации является прибыль от реализации, равная разнице между ценой реализации и себестоимостью изготовленной продукции каждого вида:

Таким образом, целевая функция примет вид:

.

Решение. Решим задачу симплекс-методом.

1. Приведем задачу в канонической форме, в которой все ограничения заданы уравнениями, а переменные неотрицательны. Так как тип неравенств «меньше или равно», то к левым частям каждого неравенства необходимо прибавить одну неотрицательную балансовую переменную: - к первому уравнению и - ко второму:

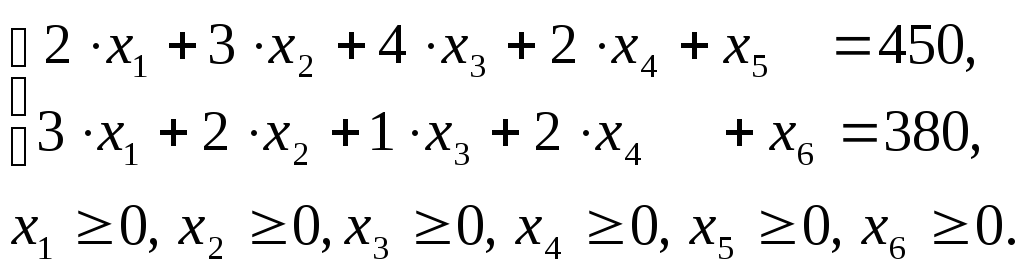
Запишем систему относительно всех переменных. Тогда в первом уравнении равен нулю коэффициент при балансовой переменной , а во втором – коэффициент при балансовой переменной :

Экономический смысл балансовых переменных и означает время работы станков 1 и 2 соответственно, которое в рамках отведенного лимита можно было использовать, но не использовалось при производстве продукции.

В целевую функцию балансовые переменные входят с коэффициентами и , равными нулю

.

2. Построение начального опорного плана.

Запишем полученную каноническую задачу в векторной форме:

,.

Здесь ,

,

- произведение вектора-строки коэффициентов целевой функции и вектора-столбца неизвестных задачи.

Единичные векторы и - линейно-независимые и образуют базис системы двумерных векторов-условий . Переменные и , соответствующие базисным векторам, являются базисными переменными, а остальные – свободными переменными, которые могут принимать произвольные значения.

Положим свободные переменные равными нулю

.

Тогда из первого уравнения ограничений найдем значение базисной переменной , а из второго – значение переменной :

.

Векторная форма системы ограничений для этих значений переменных имеет вид:

.

Поскольку положительные коэффициенты и соответствуют линейно-независимым векторам и , то по определению вектор решения с координатами:

будет невырожденным начальным опорным планом задачи. Для этого опорного плана значение целевой функции будет равно нулю

.

3. Построение первоначальной симплекс-таблицы.

Запишем полученные данные в так называемую симплекс-таблицу (таблица 4).

Первые два столбца «Шаг» и «№ строки i» являются вспомогательными.

В столбце «Шаг» запишем число 0, соответствующее нулевому шагу получения начального опорного плана .

В столбце «№ строки i» запишем порядковые номера уравнений системы ограничений (номер строки векторов-условий ). В данной задаче система ограничений состоит из двух уравнений , поэтому в столбце два элемента 1 и 2.

В столбце «Базис» записывают базисные векторы (или базисные переменные), причем в той последовательности, в которой они входят в систему ограничений. В нашем случае это векторы и , соответствующие базисным переменным и .

В столбце «С» записывают значения коэффициентов целевой функции при базисных переменных. Для начального базиса это коэффициенты и при переменных и , которые равны .

В столбце «План » записывают значения базисных переменных и найденные в процессе решения задачи компоненты оптимального плана. На начальном шаге значения базисных переменных равны правым частям уравнений системы ограничений .

В столбцах «» с номерами , число которых равно количеству переменных (в рассматриваемой задаче ), записывают соответствующие компоненты векторов-условий, которые являются коэффициентами разложения данного вектора по векторам базиса. Например, при :

.

В литературе в шапке таблицы данные столбцы обозначаются также как «», по наименованию соответствующей переменной задачи.

Сверху таблицы для удобства дальнейших вычислений можно добавить строку «Коэффициенты целевой функции », в которой над столбцами «» записывают соответствующие коэффициенты целевой функции при переменных :

.

Таблица 4. Симплекс-таблица.

Коэффициенты целевой функции					8	10	0	-5	0	0
Шаг	№ строки	Базис		План
0	1		0	450	2	3	4	2	1	0	150
	2		0	380	3	2	1	2	0	1	190
	Оценка			0	-8	-10	0	5	0	0
1	1		10	150	2/3	1	4/3	2/3	1/3	0	225
	2		0	80	5/3	0	-5/3	2/3	-2/3	1	48
	Оценка			1500	-4/3	0	40/3	35/3	10/3	0
2	1		10	118	0	1	2	2/5	3/5	-2/5
	2		8	48	1	0	-1	2/5	-2/5	3/5
	Оценка			1564	0	0	12	61/5	14/5	4/5