
- •Экономико-математические методы и модели: оптимизационные методы и модели
- •1. Введение
- •2. Общая задача математического программирования. Формы записи задач линейного программирования
- •3. Составление математических моделей простейших экономических задач
- •3. Задание целевой функции.
- •3. Задание целевой функции.
- •4. Графический метод решения задачи линейного программирования
- •4.1. Геометрическая интерпретация задачи линейного программирования
- •4.2. Алгоритм графического решения задачи линейного программирования
- •5. Симплексный метод решения задач линейного программирования
- •Построение математической модели экономической задачи.
- •3. Задание целевой функции.
- •2. Построение начального опорного плана.
- •3. Построение первоначальной симплекс-таблицы.
- •4. Вычисление оценок (значений критерия оптимальности плана).
- •Критерий оптимальности опорного плана
- •Критерий единственности опорного плана
- •5. Симплекс-критерии перехода к новому опорному плану.
- •Симплекс-критерий I включения вектора в базис
- •Симплекс-критерий II исключения вектора из базиса
- •6. Алгоритм перехода к новому базису.
- •6. Алгоритм решения задачи симплексным методом
- •6. Метод искусственного базиса
- •Особенности метода искусственного базиса
- •7. Транспортная задача (тз) линейного программирования
- •7.1. Постановка и математическая модель транспортной задачи
- •7.2. Алгоритм решения транспортной задачи
- •7.3. Опорный план транспортной задачи
- •7.3.1. Метод вычеркивания проверки опорности плана (образования цикла)
- •7.4. Построение начального опорного плана транспортной задачи
- •7.4.1. Метод северо-западного угла
- •7.4.2. Метод минимальной стоимости
- •Запишем математическую модель поставленной задачи.
- •2. Построение начального опорного плана методом минимальной стоимости.
- •Метод потенциалов.
- •Вычисление потенциалов
- •Проверка оптимальности плана
- •Переход от одного опорного плана к другому
3. Задание целевой функции.
Критерием оптимизации является доход от реализации, а целью – составление такого плана производства, который обеспечивает максимум дохода от реализации.
По условию задачи, рынок сбыта считается
неограниченным. Вся произведенная
продукция может быть продана. Поэтому,
доход от реализации
![]() равен
сумме произведений цены
равен
сумме произведений цены
![]() и
и
![]()
![]() соответствующего вида продукции на
объем ее производства (реализации).
Тогда целевую функцию
соответствующего вида продукции на
объем ее производства (реализации).
Тогда целевую функцию
![]() можно записать в виде:
можно записать в виде:
![]() или
или
![]() .
.
Совокупность целевой функции и ограничений на переменные представляет собой математическую модель экстремальной экономической задачи.
Задачу использования сырья можно легко
обобщить на случай выпуска
![]() видов продукции с использованием
видов продукции с использованием
![]() видов сырья. Пусть
видов сырья. Пусть
![]() - запасы сырья,
- запасы сырья,
![]() - расход каждого
- расход каждого
![]() -го
вида сырья на изготовление единицы
-го
вида сырья на изготовление единицы
![]() -го
вида продукции (норма расхода),
-го
вида продукции (норма расхода),
![]() - прибыль (или доход), полученная при
реализации единицы
- прибыль (или доход), полученная при
реализации единицы
![]() -го
вида продукции,
-го
вида продукции,
![]() - объем выпуска
- объем выпуска
![]() -го
вида продукции (переменные задачи).
-го
вида продукции (переменные задачи).
Необходимо составить план выпуска
продукции
![]() ,
обеспечивающий максимальную прибыль
(или доход).
,
обеспечивающий максимальную прибыль
(или доход).
Математическая модель данной задачи будет иметь вид:
![]() , (7)
, (7)
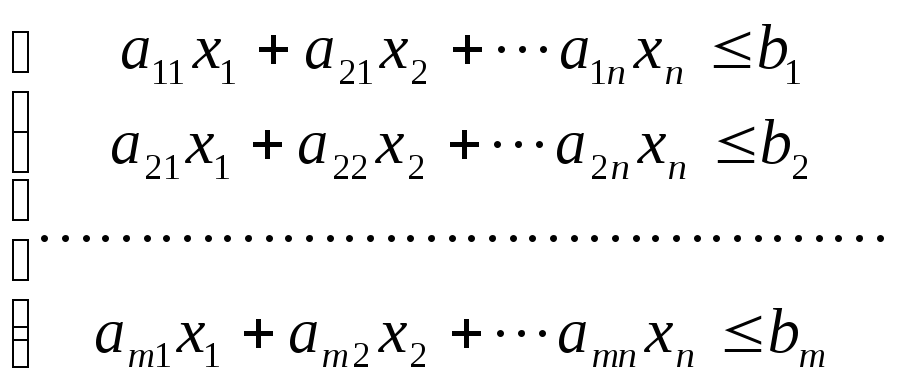 ,
(8)
,
(8)
![]() ,
(9)
,
(9)
![]() .
(10)
.
(10)
Задача 2 (составление рациона питания).
На животноводческой ферме при откорме
каждое животное ежедневно должно
получать не менее 9 единиц питательного
вещества
![]() ,
не менее 8 единиц питательного вещества
,
не менее 8 единиц питательного вещества
![]() и
не менее 12 единиц питательного вещества
и
не менее 12 единиц питательного вещества
![]() .
Для составления рациона используют два
вида корма. Содержание единиц питательных
веществ в 1 кг корма приведены в таблице
2. Необходимо составить суточный рацион,
обеспечивающий получение необходимого
количества питательных веществ при
минимальных денежных затратах.
.
Для составления рациона используют два
вида корма. Содержание единиц питательных
веществ в 1 кг корма приведены в таблице
2. Необходимо составить суточный рацион,
обеспечивающий получение необходимого
количества питательных веществ при
минимальных денежных затратах.
Таблица 2.
|
Питательные вещества |
Количество единиц питательных веществ в 1 кг корма |
Необходимое количество питательного вещества (ед) |
|
|
1. Корм 1 |
2. Корм 2 |
||
|
1.
2.
3.
|
3 1 1 |
1 2 6 |
9 8 12 |
|
Стоимость 1 кг корма (у.е.) |
4 |
6 |
|
1. Выбор переменных. Переменными
данной задачи являются суточные объемы
![]() корма 1 и корма 2 в рационе. Обозначим их
корма 1 и корма 2 в рационе. Обозначим их
![]() и
и
![]() соответственно.
соответственно.
2. Система ограничений. Так как суточный рацион должен удовлетворять требуемой питательности, то количество единиц питательных веществ, содержащихся в обоих кормах должно быть не меньше требуемого. В соответствие со значениями содержания питательных веществ в 1 кг корма, указанных в таблице, получим следующую систему ограничений
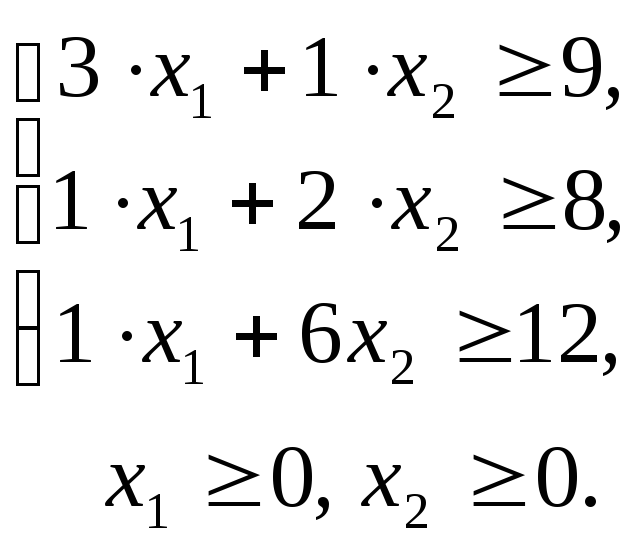
Ограничение на неотрицательность
переменных следует из того, что при
отсутствии корма 1 в рационе значение
![]() .
Если корм присутствует в рационе, то
.
Если корм присутствует в рационе, то
![]() .
.
