7.2. Алгоритм решения транспортной задачи
Алгоритм решения транспортной задачи является итерационным и во многом совпадает с алгоритмом симплекс-метода.
1. Привести транспортную задачу к закрытому (сбалансированному) типу.
2. Построить начальное опорное решение.
3. Проверить оптимальность плана транспортной задачи.
4. Если критерий оптимальности выполняется, то задача решена.
5. Если критерий оптимальности не выполняется, то перейти к новому опорному плану и пункту 3.
Рассмотрим подробно каждый шаг алгоритма.
1. Если условие (52) баланса запасов и потребностей не выполняется, то задача является открытой и ее необходимо привести к задаче закрытого типа.
В случае, когда общее количество запасов
продукции у поставщиков превышает общий
спрос потребителей
,
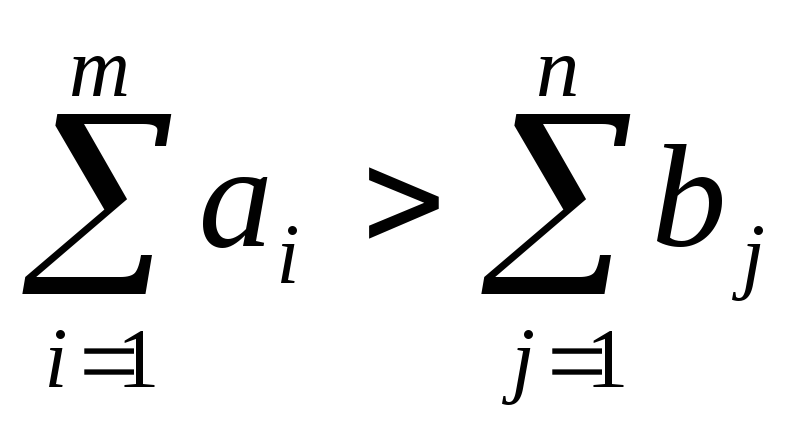то необходимо ввести фиктивного
потребителя
,
потребности которого определяются
выражением:
.
(55)
В случае, когда общий спрос потребителей
превышает общее количество запасов
продукции у поставщиков общий спрос
потребителей
,
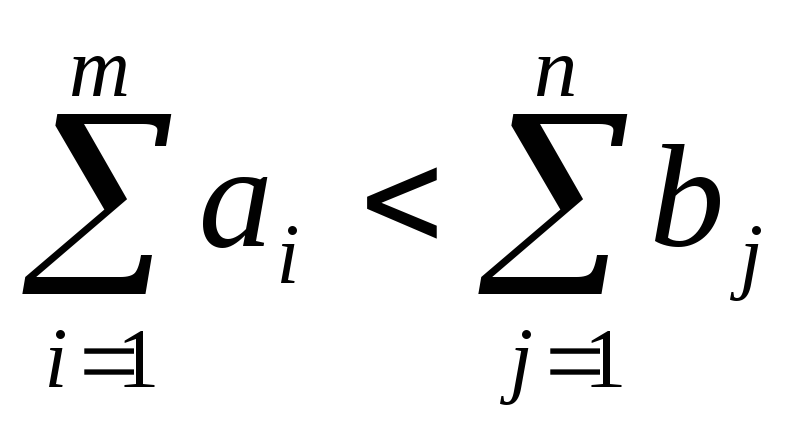то необходимо ввести фиктивного
поставщика
,
запасы которого определяются выражением:
.
(56)
Тарифы на перевозку фиктивного
потребителя и фиктивного поставщика
считаются равными нулю:
и
.
7.3. Опорный план транспортной задачи
Система ограничений (49)-(51)
закрытой транспортной задачи состоит
из
уравнений подсистемы (49) и
уравнений подсистемы (50). То есть, содержит
уравнений, связанных соотношением
баланса (52) и
неотрицательных неизвестных
.
Если преобразовать систему уравнений,
прибавив к любому уравнению каждой из
подсистем (49) и (50) остальные уравнения
соответствующей подсистемы, то получим
эквивалентную систему уравнений,
содержащую два одинаковых уравнения.
Это означает, что система
уравнений линейно зависимая. Если
отбросить одно из одинаковых уравнений,
то в общем случае получим систему из
линейно независимых уравнений с
неотрицательными переменными.
Следовательно, ранг
системы из
векторов условий транспортной задачи
на единицу меньше количества уравнений
.
Базисными переменными будут
неотрицательных переменных
,
а остальные
переменные – свободными, которые можно
положить равными нулю.
Определение. Невырожденным
опорным планом транспортной
задачи называется план, содержащий
положительных базисных переменных,
а остальные
небазисные переменные равны нулю.
Если какая-нибудь из
базисных переменных равна нулю,
то опорный план называется вырожденным.
Определение. Клетки распределительной
таблицы, в которых записаны положительные
значения перевозок
,
называются базисными
или занятыми. Если опорный
план невырожденный,
то количество таких клеток равно
.
Если опорный план вырожденный, то
некоторые из
базисных переменных и соответствующих
перевозок
,
будут равны нулю, который называют
«базисным» нулем. Для того чтобы
отличать базисные нулевые перевозки
от нулевых перевозок, соответствующих
небазисным свободным переменным, в
распределительную таблицу заносятся
только «базисные» нули, которые
обозначаются
.
Базисным переменным, входящим в опорный
план, соответствует система, состоящая
из
линейно-независимых векторов условий.
Для проверки опорности плана (линейной
независимости векторов условий при
базисных переменных) транспортной
задачи, записанной в виде распределительной
таблицы, используют понятие цикла.
Определение. Цепью называется совокупность клеток распределительной таблицы, в которой две и только две клетки расположены в пределах одной строки или одного столбца.
Определение. Циклом называется такая цепь, в которой первая и последняя клетки принадлежат одной строке или одному столбцу.
С геометрической точки зрения цепь представляет собой разомкнутую ломаную линию (рис.5) , а цикл – замкнутую ломаную линию.
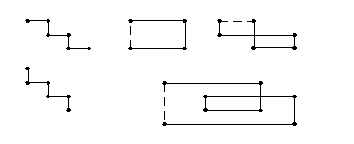
а) в) г)
б) д)
Рис. 5. Геометрическое изображение цепей (а, б) и циклов (в, г, д)
Признак опорности плана. План транспортной задачи, записанной в виде распределительной таблицы, является опорным, если он обладает свойством ацикличности, то есть, когда из занятых (базисных) клеток нельзя построить цикл.
На практике для проверки возможности образования цикла используют метод вычеркивания.