7. Транспортная задача (тз) линейного программирования

7.1. Постановка и математическая модель транспортной задачи

Транспортная задача является специфической задачей линейного программирования и применяется для определения наиболее экономного оптимального плана грузоперевозок однородной продукции от поставщиков к потребителям.

Пусть некоторый однородный продукт (груз) сосредоточен у поставщиков в количествах (запас продукции) соответственно. Данный продукт необходимо доставить потребителям в количествах (спрос на продукцию). Известны стоимости перевозки (тарифы) единицы продукции от -го поставщика к -му потребителю .

Требуется составить такой план перевозок, при котором полностью вывозятся запасы продукции всех поставщиков, полностью удовлетворяется спрос на продукцию всех потребителей, а суммарные затраты на перевозку всех грузов минимальны.

Обозначим через количество единиц продукции, планируемое к перевозке от каждого -го поставщика к каждому -му потребителю, то есть, объемы перевозок, которые являются переменными задачи. Тогда, условия задачи можно записать в виде распределительной таблицы, которую называют также матрицей планирования (таблица 6).

Таблица. 6. Матрица планирования

Поставщики	Потребители				Запасы
			…
			…
			…
	…	…	…	…	…
			…
Потребности			…

Матрица планирования состоит из коэффициентов матрицы тарифов и матрицы перевозок

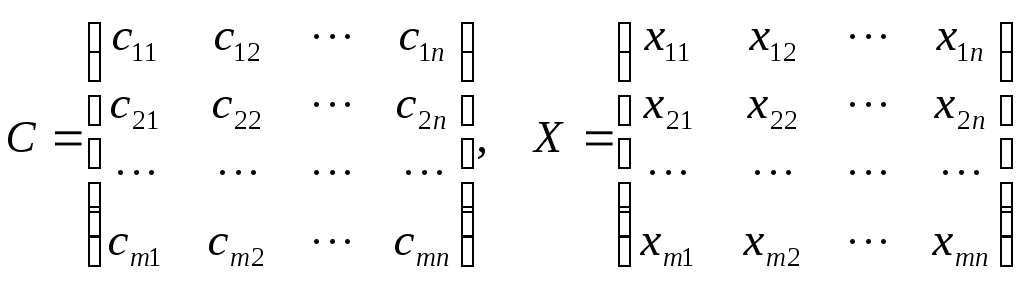. (47)

В последнем столбце указано количество запасов продукции у поставщиков, а в последней строке - потребности потребителей в этой продукции.

Составим математическую модель транспортной задачи. Стоимость перевозки продукции, в количестве единиц от -го поставщика к -му потребителю равна произведению тарифа на перевозку единицы продукции на объем перевозки .

Тогда целевая функция, равная сумме затрат на перевозку всех грузов (транспортных расходов), должна стремиться к минимуму:

. (48)

По условию задача минимизации транспортных расходов имеет следующие ограничения:

а) весь груз (запас) от каждого из поставщиков должен быть вывезен:

(49)

(суммы элементов строк матрицы планирования);

б) потребности каждого из потребителей должны быть удовлетворены:

(50)

(суммы элементов столбцов матрицы планирования);

в) должны выполняться условия неотрицательности объемов перевозимых грузов:

. (51)

Таким образом, математическая формулировка транспортной задачи состоит в следующем:

найти такие значения переменных , которые удовлетворяют системе ограничений (49), (50), условиям (51) неотрицательности переменных и обеспечивают минимум целевой функции (48).

Транспортные задачи бывают двух типов: закрытие и открытые.

Определение. Транспортная задача называется сбалансированной или закрытой, если общее количество запасов продукции у поставщиков равно общим потребностям всех потребителей, то есть

, (52)

Определение. Транспортная задача называется несбалансированной или открытой, если:

общее количество запасов продукции у поставщиков превышает общий спрос потребителей

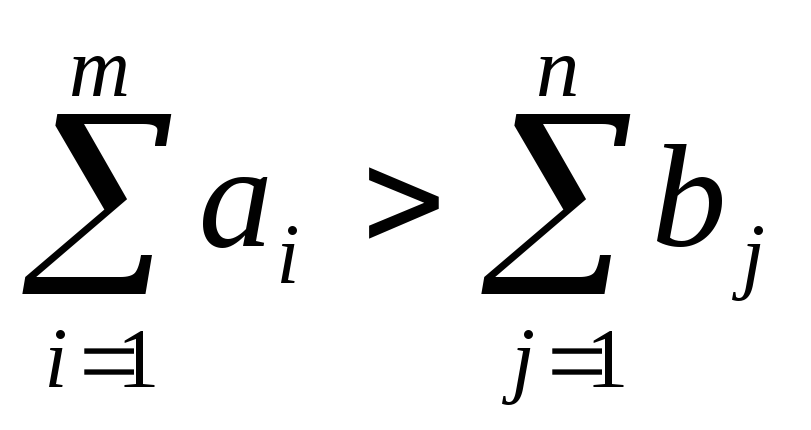; (53)

общий спрос потребителей превышает общее количество запасов продукции у поставщиков:

. (54)

Методы решения разработаны только для ТЗ закрытого типа. Однако открытые задачи можно привести к закрытым.

Определение. Планом транспортной задачи называется любое неотрицательное решение системы ограничений (49)-(51) , которое определяется матрицей перевозок (47): .

Определение. Оптимальным планом транспортной задачи называется план , при котором целевая функция (48) достигает своего минимального значения.

Теорема (условие существования решения транспортной задачи). Для того чтобы транспортная задача имела решение необходимо и достаточно, чтобы суммарный объем запасов был равен суммарному объему потребностей:

,

то есть, задача должна быть сбалансированной или закрытой.

Транспортная задача является задачей линейного программирования и может быть решена симплекс-методом. Однако, специфика системы ограничений (каждая неизвестная входит только в два уравнения системы ограничений (49) и (50), а коэффициенты при неизвестных равны единице) позволила разработать более эффективный метод ее решения, который называется методом потенциалов.