Пересечение поверхности с прямой линией

62. На прямой (BC) найти точки, удалённые от точки А на 25мм.

B2

A2

C2

C1

B1

A1

63. Построить точки пересечения прямых ℓ и m с данными поверхностям.

ℓ₂

а) б)

m2

ℓ₂

ℓ₁

m1

ℓ₁

ℓ₂

В

ℓ₂

h2

)

Г)

h2

h1

ℓ₁

h1

ℓ₁

Построение линии пересечения поверхностей способом вспомогательных плоскостей

/2 поз. Задача./

64. На поверхности конуса построить множество точек ,удалённых от прямой ℓ на 15мм.

ℓ₂

ℓ₁

65. Построить множество точек ,удалённых от точки О/O1,O2/ на 30мм и от прямой m/m1,m2/ на 25мм.

O2

m2

m1.

O1

66. Построение линии пересечения поверхностей способом вспомогательных плоскостей.

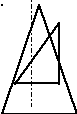
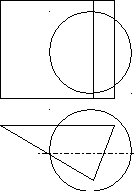
67.Построить линии пересечения поверхностей при помощи

вспомогательных сфер

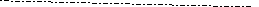
Комплексные задачи

68. Найти прямую, равноотстоящую а) от точек А, В, и D.

б

B2

C2

) от точек А,В,С и D

D2

A2

B1

D1

A1

C1

69.Определить угол между прямой “m” и плоскостью Г (а ∩ в)

m2

a2

b2

a1

b1

m1

7

S2

B2

0. Через точку “S” повести прямую, наклонённую к плоскости П1 под углом 65⁰ и пересекающую прямую АВ.

A2

A1

B1

S1

7

В2

1. Через точку А провести прямую, перпендикулярную прямым “m” и “k”.

k2

m2

m1

k1

В1

7

A1

2. На поверхности шара построить геометрическое место точек, равноудалённых от точек А и В.

A1

A1

A1

73. Построить равнобедренный треугольник АВС, если основание принадлежит прямой “с”, а боковая сторона – прямой “a”

a2

/AB/=50

A2

c2

a1

A1

c1

74. По заданным направлениям катета “в” и гипотенузы “c”

построить треугольник, если длина гипотенузы 60 мм.

b2

c2

c1

b1

75.Через точку А провести прямую, параллельную плоскости Г(а в) и перпендикулярную прямой “m”.

A2

a2

m2

b2

a1

m1

b1

A1

76. На прямой “m” найти точку А, удалённую от плоскости Г (а ∩ в) на расстояние 25мм.

a2

m2

b2

a1

m1

b1

7

A2

7. Построить проекции правильного треугольника АВС, если ВС принадлежит “m”.

m2

m1

A1

78. Через прямую “n”провести плоскость, удалённую от прямой “m” на 20мм m n.

n2

m2

m1

n1

79. Определить кратчайшее расстояние MN между скрещивающимися прямыми “m” и ”n”.

m2

n2

n1

m1

80. Построить отрезок MN , являющийся кратчайшим расстоянием от плоскости Г (а ∩ в) до сферы с центром “S”и R25

a2

b2

S2

a1

b1

S1

8

A1

1.Построить прямые, проходящие через точку “А” и пересекающие “m” под углом 50⁰

A1

A1

A1

8

A1

A2

m1

m2

2. Построить проекции квадрата ABCD, если BC Є m

31