
- •Пояснительная записка к курсовому проекту
- •1. Теоретическая часть
- •История
- •Функционирование
- •Политика записи при кэшировании
- •Кэширование интернет-страниц
- •Кэширование результатов работы
- •Кэш центрального процессора
- •Уровни кэша
- •Организация кэш
- •Кэширование внешних накопителей
- •Кэширование, выполняемое операционной системой
- •Алгоритм работы кэша с отложенной записью
- •Алгоритм вытеснения
- •2. Практическая часть
- •Задание на проектирование алу
- •Проектирование операционного автомата алу
- •Определение форматов данных
- •2.2.2 Объединенная гса деления и дизъюнкции
- •2.2.3. Разработка структуры операционного автомата
- •2.2.4. Список микроопераций и логических условий, реализуемых в оа
- •2.2.5 Микропрограмма выполняемых в алу операций
- •Проектирование управляющего автомата алу
- •2.3.1 Определение формата микрокоманд
- •Кодирование микроопераций и логических условий
- •Структурная схема управляющего автомата
- •2.3.4 Содержимое пзу микропрограмм
2. Практическая часть
-
Задание на проектирование алу
Вариант 1-14
Разработать арифметико-логическое устройство (АЛУ), реализующее деление без восстановления остатка в прямом коде и дизъюнкцию и отображающее признаки результата: OV – признак арифметического переполнения, P – признак четности числа единиц в результате.
Тип управляющего автомата – программируемая логика, различные форматы для операционных микрокоманд и микрокоманд перехода, принудительная адресация.
-
Проектирование операционного автомата алу
-
Определение форматов данных
-
В арифметической операции деления участвуют операнды A – делимое и B – делитель. Результат операции C – частное. Кроме того, устройство должно формировать признаки результата – двоичные переменные:
-
OV – признак арифметического переполнения;
-
P – признак четности числа единиц в результате.
Алгоритм операции деления разрабатывается для 16 – разрядных двоичных чисел с фиксированной запятой, представленных в прямом коде. Знак числа кодируется в старшем (нулевом) разряде числа, запятая фиксирована после знакового разряда, таким образом, все числа могут быть только дробными.
0
15
1
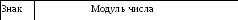
Рис. 2.1. Представление числа в прямом коде
В операциях участвуют следующие переменные:
-
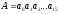 ‑ первый операнд (делимое);
‑ первый операнд (делимое); -
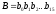 ‑ второй операнд (делитель);
‑ второй операнд (делитель); -
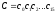 ‑ результат операции (частное), в
процессе выполнения алгоритма переменная
‑ результат операции (частное), в
процессе выполнения алгоритма переменная
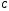 используется для хранения остатка;
используется для хранения остатка; -
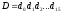 ‑ переменная, в которой в процессе
деления накапливаются цифры частного;
‑ переменная, в которой в процессе
деления накапливаются цифры частного; -
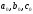 ‑ знаковые разряды.
‑ знаковые разряды.
В операции дизъюнкции положение запятой
и знак игнорируются, операция выполняется
над 16-разрядными двоичными векторами
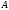 и
и
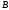 .
Результат операции представлен в той
же форме, что и для арифметической
операции деления:
.
Результат операции представлен в той
же форме, что и для арифметической
операции деления:
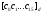 .
.
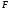 -
тип выполняемой операции (0 – арифметическая,
1 – логическая).
-
тип выполняемой операции (0 – арифметическая,
1 – логическая).
2.2.2 Объединенная гса деления и дизъюнкции
В прямых кодах удобнее делить модули чисел. Знак результата не зависит от соотношения модулей делимого и делителя и определяется по выражению (2.1):
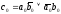 (2.1)
(2.1)
Деление чисел с фиксированной запятой в заданном формате невозможно, если модуль делимого не меньше модуля делителя. Поэтому сначала следует проверить соотношение операндов путем вычитания делителя из делимого. Если разность окажется положительной, то можно формировать признак переполнения OV = 1 и завершать операцию. В противном случае модуль частного оказывается меньше 1, т.е. переполнение отсутствует и деление возможно.
Алгоритм предусматривает формирование
знака результата согласно формуле (2.1)
и сохранение его временно в переменной
 .
После этого производится деление модулей
чисел (знаки операндов обнуляются).
.
После этого производится деление модулей
чисел (знаки операндов обнуляются).
Сначала производится пробное вычитание
делителя из делимого. Поскольку знаки
операндов – 0, то появление 1 в знаковом
разряде разности означает, что
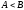 ,
и можно продолжать деление (целая часть
частного равна 0). При
,
и можно продолжать деление (целая часть
частного равна 0). При
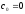 деление невозможно – формируется
признак переполнения.
деление невозможно – формируется
признак переполнения.
В процессе получения цифр частного
значение очередного остатка принимает
переменная
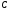 .
Независимо от знака остатка она копируется
в переменную
.
Независимо от знака остатка она копируется
в переменную
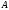 ,
которая затем увеличивается вдвое путем
сдвига влево на один разряд. В зависимости
от знака переменной
,
которая затем увеличивается вдвое путем
сдвига влево на один разряд. В зависимости
от знака переменной
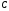 (знака остатка) формируется очередная
цифра переменной
(знака остатка) формируется очередная
цифра переменной
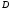 (частного) и принимается решение о
действии на следующем шаге – добавлять
или вычитать делитель из сдвинутого
остатка. После арифметической операции
выполняется сдвиг влево частного
(частного) и принимается решение о
действии на следующем шаге – добавлять
или вычитать делитель из сдвинутого
остатка. После арифметической операции
выполняется сдвиг влево частного
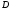 (освобождается место для очередной
цифры частного), изменяется счетчик
цифр частного и проверяется условие
выхода из цикла – получение шестнадцати
цифр частного, включая самую первую
цифру – «0 целых», на место которой
копируется знак частного из переменной
(освобождается место для очередной
цифры частного), изменяется счетчик
цифр частного и проверяется условие
выхода из цикла – получение шестнадцати
цифр частного, включая самую первую
цифру – «0 целых», на место которой
копируется знак частного из переменной
 .
.
Алгоритм предусматривает формирование
признака четности числа единиц в
результате – флаг
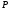 .
Если
.
Если
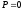 ,
то число единиц в результате четно, если
,
то число единиц в результате четно, если
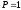 - нечетно.
- нечетно.
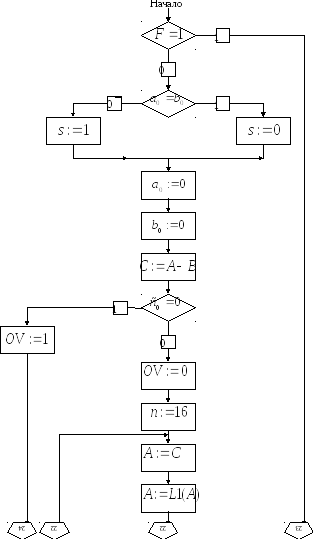
Объединенная граф-схема алгоритмов деления без восстановления остатка и дизъюнкции показана на рис. 2.2.


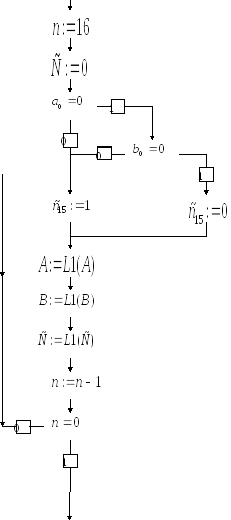
22
21
24
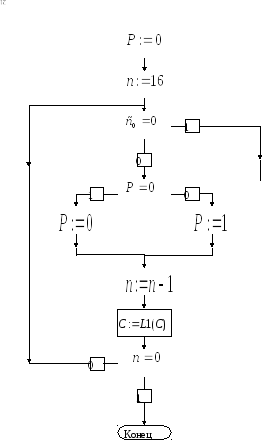
23
Рис. 2.2. Объединенная граф – схема алгоритмов дизъюнкции и деления без восстановления остатка
