3. Интервальные оценки и алгоритм построения

В отличие от точечных оценок типа ^*_n интервальные оценки задают интервал значений где оцениваемый параметр находится с заданной вероятностью, т.е. это оценки типа Р( ^*_n) = 

Надежностью оценки (доверительной вероятностью) называется вероятность , с которой оцениваемый параметр находится в интервале

^*_n_ ^*_n_ .

Полуширина доверительного интервала _ называется точностью оценки, соответствующей надежности . Для построения доверительного интервала (нахождения по  величины _) необходимо знать закон распределения оценки случайной величины ^*_n.

Пусть в выборке х_В = {х₁, х₂, …х_n,} наблюдается нормальная случайная величина Х=N(a,) c неизвестными параметрами распределения а и . Построим доверительный интервал для математического ожидания а:

`х<sub>В</sub> -<sub></sub>a `х_В _ ,

принимая за точечную оценку а, величину а* =`х<sub>В</sub> и учитывая что величина (`Х_В -а )_/S = t_n-1 имеет распределение Стьюдента с n-1 степенью свободы. Решение уравнение Р( `Х_В а) = относительно при заданном эквивалентно решению уравнения

или .

Его решение получим в виде _=t_gS/, где t_g= t_g(n-1) двухсторонняя квантиль Стьюдента (рис. 12.2).

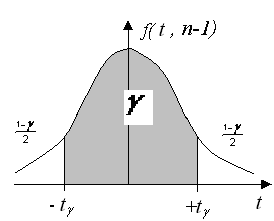
Рис. 12.2 Двухсторонняя квантиль Стьюдента.

Построим теперь доверительный интервал для среднеквадратического отклонения 

S -_ S _ .

Принимая за оценку  величину ^  S и учитывая, что величин S/ = _n-1 имеет -распределение с n - 1 степенью свободы. Решение уравнение Р( S) =  относительно  при заданном эквивалентно решению уравнения

,

где обозначено, а , тогда получим его решение в виде ,

где величины являются правосторонними “хи-квадрат” квантилями (рис.12.3).

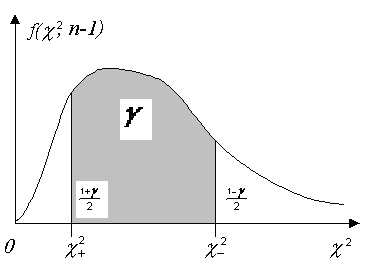
Рис. 12.3 Двухсторонняя “хи-квадрат”квантиль.

Пример: Пусть наблюдается выборка объемом n =16 со средним выборочным значением `х_В =20,2 и выборочной дисперсией D_B = 0,6. Построить доверительные интервалы для неизвестного математического ожидания а и среднеквадратического отклонения для надежности 

Исправленная дисперсия S² = (16/15)*0,6=0,64, а исправленное выборочное среднеквадратическое отклонение S = 0,8.

По таблице квантилей для распределения Стьюдента в приложении 3 находим t_g=t_g(1-) = 2,13, тогда _=t_gS/= 2,13* 0,8/4=0,43 и доверительный интервал для математического ожидания а будет 20,2-0,43< a <20,2+0,43 или 19,77< a <20,63.

По таблице для квантилей ²–распределения в приложении 4 находим и тогда 0,591< <1,238

В указанных интервалах истинные значения неизвестных параметров находятся с вероятностью 0,95.

80