2. Таблицы распределения выборочных величин

Обычно выборочные распределения задаются таблично в виде право-сторонних функций распределения и/или обратных к ним квантилей известны [10] и приводятся в Приложениях 2-5.

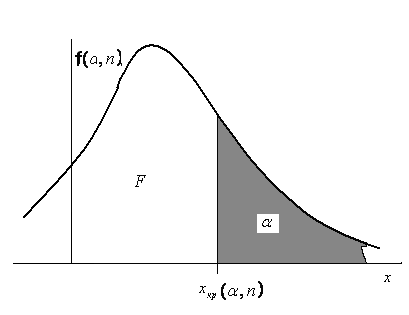
Рис.11.3 Правосторонняя квантиль

В статистическом комплексе программ MS Exel эти распределения представлены следующими функциями:

- правостороннее распределение Пирсона,

- правосторонняя квантиль Пирсона,

- правостороннее Т-распредел. Стьюдента,

- двухстороннее Т -распредел. Стьюдента,

- двухсторонняя Т -квантиль Стьюдента,

- правостороннее F-распределение Фишера,

- правосторонняя квантиль Фишера.

Для работы с нормальной случайной величиной имеются следующие полезные функции:

- весовая функция нормального распределен;

- интегральная функция нормального распред;

- обратная интегральная функция;

- функция Гаусса стандартная;

- Функция Лапласа стандартная.

Лекция № 12

Статистические оценки параметров распределения

Пусть распределение наблюдаемой случайной непрерывной величины Х (признак генеральной совокупности), задается функцией плотности вероятности, где  параметр или параметры распределения. Допустим, что вид функции известен или ограничен некоторым классом функций, а параметр неизвестен и должен быть оценен по выборке , где n – объем выборки.

1. Точечные оценки.

Точечной статистической оценкой параметров распределения или характеристик наблюдаемой случайной величины Х, называется построенная по данным выборки объема n величина:

.

Оценка ^*_n является так же случайной величиной, т.к. зависит от случайной выборки, поэтому ее можно представить как функцию от случайных величин ^*_n =^*_n(Х₁, Х₂,.., Х_n), где Х_i независимые случайные величины, распределенные так же как и сама величина Х. Для того, что бы оценки, получаемые по данным различных выборок соответствовали истинному значению параметра , оценка должна удовлетворять следующим требованиям.

Оценка должна быть несмещенной, т.е. ее математическое ожидание должно совпадать с истинным значением параметра для любого объема n

М(^*_n) = .

или хотя бы асимптотически несмещенной: .

Оценка должна быть состоятельной, т.е. с ростом объема выборки оценка должна сходится по вероятности к истинному значению параметра:

для любого > 0 .

Для состоятельности оценки достаточно выполнения следующего:

,

тогда из неравенства Чебышева для случайной величины ^*_n

следует состоятельность оценки.

Построенная оценка для использования на практике должна быть эффективной, т.е. ее дисперсия должна быть минимальной среди всех возможных оценок при фиксированном объеме выборки:

D(^*_n,эф) = min D(^*_n).

Величину дисперсии эффективной оценки можно найти используя неравенство Рао-Крамера

,

где 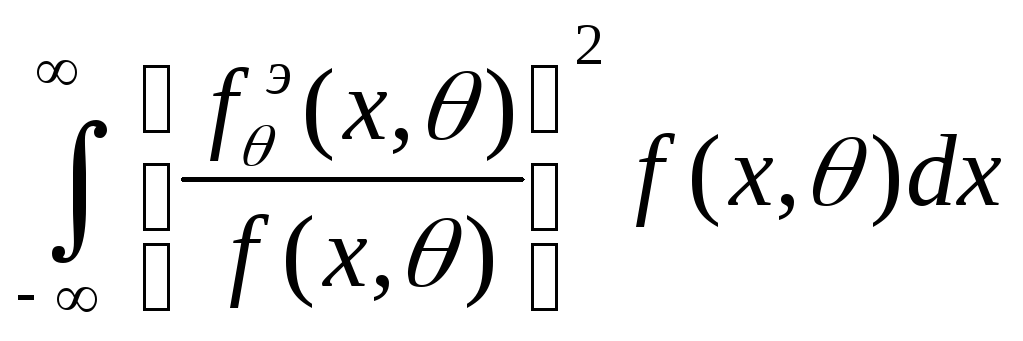- информация Фишера. Коэффициент эффективности оценки k_эф(^*)= D(^*_n,эф)/ D(^*_n) показывает степень эффективности оценки ^*, если , то говорят об асимптотической эффективности оценки.

Отметим, что на практике не всегда удается удовлетворить всем перечисленным требованиям к оценке, но введенные свойства оценок всегда позволяют проранжировать имеющиеся оценки по их качеству.

В качестве примера рассмотрим оценки математического ожидания М(Х) = m и дисперсии D(Х) = ² наблюдаемой случайной величины X. Построим точечные оценки:

,

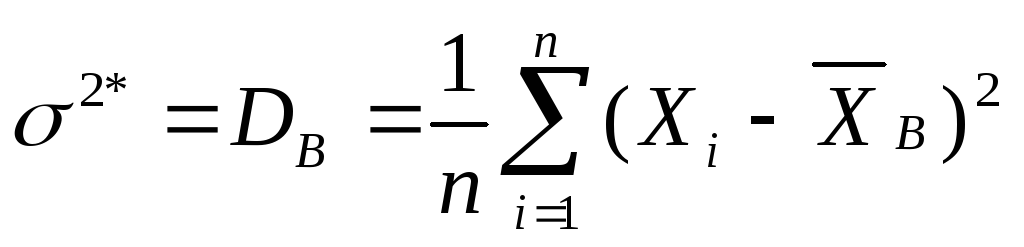
и рассмотрим их свойства. Поскольку М(Х_i) = m и D(Х_i) = ² то можно вычислить, что для оценки m^* справедливо:

М(m^*) = m; D(m^*) = ² /n  0 при n  

Из этого следует несмещенность и состоятельность оценки m^*.

Рассматривая же оценку ^2* можно получить:

; 

Из чего следует не только состоятельность, но и смещенность оценки ^2*. Смещеность оценки здесь легко может быть исправлена. Рассмотрим оценку:

.

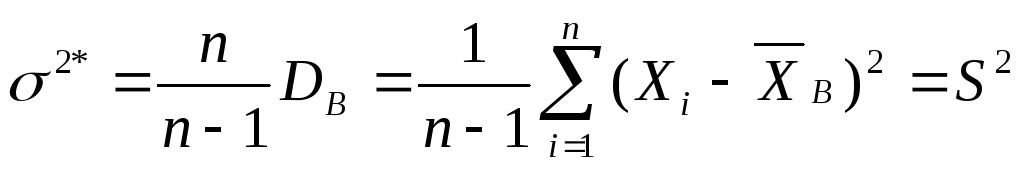Оценка ^2*=S² является уже несмещенной и состоятельной оценкой. Величина S² называется исправленной (уточненной) выборочной дисперсией, а величина S исправленным среднеквадратическим выборочным отклонением (выборочный стандарт).

В заключении напомним что относительная частота w_n появления события в независимых испытаниях Бернулли является несмещенной, состоятельной и эффективной оценкой неизвестной вероятности этого события р^*=w_n (теорема Бернулли), а эмпирическая функция выборочного распределения является состоятельной несмещенной оценкой неизвестной функцией распределения наблюдаемой случайной величины (теорема Гливенко).