
- •1. Закон распределения дискретной случайной величины
- •2. Пример распределения дискретной случайной величины. Биномиальное распределение
- •3. Пример распределения дискретной случайной величины. Распределение Пуассона
- •4. Пример распределения дискретной случайной величины. Геометрическое распределение
- •Лекция № 6
- •1. Функция распределения непрерывной и дискретной случайной величины
- •1. Свойства функции распределения
- •3. Плотность распределения вероятностей непрерывной случайной величины
- •1. Равномерное распределение
- •2. Нормальное распределение
- •3. Показательный (экспоненциальный) закон распределения
- •4. Логарифмически-нормальное распределение
- •5. Вейбуловское распределение
- •1. Математическое ожидание. Дискретные случайные величины
- •2. Математическое ожидание. Непрерывные случайные величины
- •3. Дисперсия и среднее квадратическое отклонение случайной величины
- •4. Моменты распределения случайной величины
- •1. Теорема Чебышева
- •2. Центральная предельная теорема
- •3. Теорема Бернулли
1. Равномерное распределение
Определение. Случайная величина с плотностью вероятности
 ,
где
,
где
![]() ,
,
называется равномерно распределённой величиной.
Равномерный закон распределения используется: при анализе ошибок измерения, когда проводятся численные расчёты; в ряде задач массового обслуживания.
Найдём величину
![]() из условия
из условия
![]() (свойство
(свойство
![]() плотности вероятности):
плотности вероятности):
 .
.
Поэтому
![]() ,
а плотность вероятности
равномерно
распределённой величины имеет вид:
,
а плотность вероятности
равномерно
распределённой величины имеет вид:
 .
.
Найдём также
функцию распределения равномерно
распределённой величины. По свойству
![]() для плотности вероятности:
для плотности вероятности:
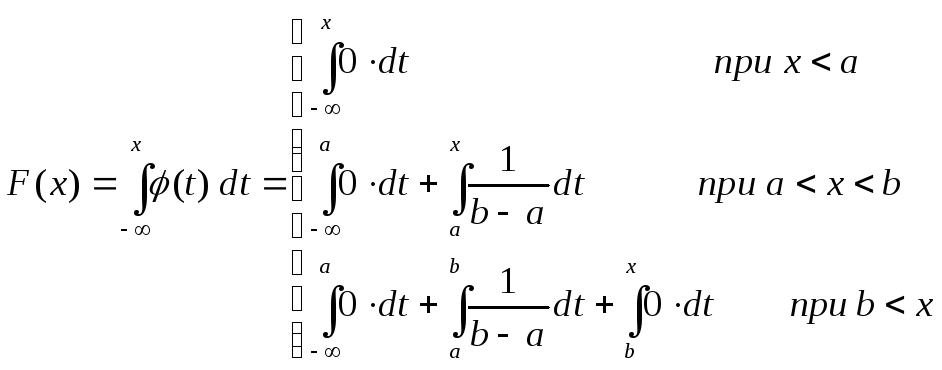 =
=
 .
.
Графики функций
![]() и
и
![]() приведены ниже на рис. 7.1. На графике для
функции
приведены ниже на рис. 7.1. На графике для
функции
![]() четыре стрелки означают, что левый или
правый пределы не достижимы функцией
в соответствующей точке.
четыре стрелки означают, что левый или
правый пределы не достижимы функцией
в соответствующей точке.

Рис. 7.1. Равномерное распределение.
_______________
Пример.
Поезда
метрополитена идут регулярно с интервалом
![]() минуты. Пассажир выходит на платформу
в случайный момент времени. Какова
вероятность того, что ждать пассажиру
придётся не более полминуты.
минуты. Пассажир выходит на платформу
в случайный момент времени. Какова
вероятность того, что ждать пассажиру
придётся не более полминуты.
Решение.
Пусть случайная величина
![]() - время ожидания пассажира. Тогда её
плотность
вероятности равна:
- время ожидания пассажира. Тогда её
плотность
вероятности равна:
 .
.
Поэтому
по свойству
![]() для плотности вероятности получим:
для плотности вероятности получим:
 .
.
2. Нормальное распределение
Определение. Случайная величина имеет нормальный закон распределения (закон Гаусса), если её плотность распределения вероятностей имеет вид:
 ,
,
где
![]() и
и
![]() - параметры распределения (
- параметры распределения (![]() ).
).
Нормальный закон распределения наиболее часто встречается на практике. Главная его особенность – он является предельным законом, к которому приближаются другие законы распределения (при типичных условиях).
Плотность
вероятности
![]() - функция, похожая на колокол (рис.7.2).
Зависимость от параметров такова. При
уменьшении только параметра
- функция, похожая на колокол (рис.7.2).
Зависимость от параметров такова. При
уменьшении только параметра
![]() ,
график функции вытягивается и поднимается
вверх по оси ординат. А при увеличении
только параметра
,
график функции вытягивается и поднимается
вверх по оси ординат. А при увеличении
только параметра
![]() ,
график симметрично передвигается вправо
вдоль оси абсцисс:
,
график симметрично передвигается вправо
вдоль оси абсцисс:

Рис. 7.2. Функция плотности распределения нормальной величины.
Функция распределения
![]() нормального распределения
нормального распределения
![]()

имеет следующий вид, изображенный на рис. 7.3:

Рис. 7.3. Функция распределения нормальной величины
а) Правило «трёх сигм»
Найдём вероятность
того, что изучаемая случайная величина
(распределённая нормально) примет
значение в пределах от
![]() до
до
![]() :
:
![]()
 .
.
Для этого воспользуемся известным из математического анализа свойством определённого интеграла:
![]()
и, используя ещё одно свойство:
![]() ,
,
окончательно получим:
![]() .
.
Этим равенством
и воспользуемся (при условии, что роль
![]() играет параметр
играет параметр
![]() из нормального закона)
из нормального закона)
![]()
 .
.
Далее сделаем
замену
![]() в определённых интегралах (тогда
в определённых интегралах (тогда
![]() или
или
![]() ):
):
![]()


 ,
,
где функция
![]() ,
функция Лапласа
,
функция Лапласа
 ,
она затабулирована и приводится в
приложении 2. В частном случае, когда
интервал симметричен относительно
точки
,
она затабулирована и приводится в
приложении 2. В частном случае, когда
интервал симметричен относительно
точки![]() ,
эта формула выглядит так:
,
эта формула выглядит так:
![]()
![]()
![]()
или так:
![]()
![]() .
.
Отсюда правило
«трёх сигм» выводится следующим образом.
Рассмотрим вероятность того, что
изучаемая случайная величина
(распределённая нормально) примет
значение в пределах от
![]() до
до
![]() :
:
![]()
![]() .
.
Из таблицы для
функции Лапласа находим, что
![]() ,
поэтому
,
поэтому
![]()
![]() ,
,
т.е. вероятность
встретить значение изучаемой случайной
величины именно на интервале
![]() ужасно велика -
ужасно велика -
![]() !!!
!!!
