
- •1. Закон распределения дискретной случайной величины
- •2. Пример распределения дискретной случайной величины. Биномиальное распределение
- •3. Пример распределения дискретной случайной величины. Распределение Пуассона
- •4. Пример распределения дискретной случайной величины. Геометрическое распределение
- •Лекция № 6
- •1. Функция распределения непрерывной и дискретной случайной величины
- •1. Свойства функции распределения
- •3. Плотность распределения вероятностей непрерывной случайной величины
- •1. Равномерное распределение
- •2. Нормальное распределение
- •3. Показательный (экспоненциальный) закон распределения
- •4. Логарифмически-нормальное распределение
- •5. Вейбуловское распределение
- •1. Математическое ожидание. Дискретные случайные величины
- •2. Математическое ожидание. Непрерывные случайные величины
- •3. Дисперсия и среднее квадратическое отклонение случайной величины
- •4. Моменты распределения случайной величины
- •1. Теорема Чебышева
- •2. Центральная предельная теорема
- •3. Теорема Бернулли
Лекция № 6
Непрерывные случайные величины
1. Функция распределения непрерывной и дискретной случайной величины
Начнём с определения.
Определение. Непрерывной случайной величиной называется переменная, которая может принимать случайным образом любые значения в некотором интервале числовой оси.
Обозначение.
Обозначать непрерывные случайные
величины будем латинскими буквами
![]() ,
,
![]() ,
,
![]() ,...
,...
_______________
Пример.
Пусть между двумя населёнными пунктами
![]() и
и
![]() протянута телефонная линия, расстояние
между ними равно
протянута телефонная линия, расстояние
между ними равно
![]() .
Тогда точку возможного
обрыва линии будем характеризовать
случайной величиной
.
Тогда точку возможного
обрыва линии будем характеризовать
случайной величиной
![]() ,
которая принимает значения на интервале
от нуля до
,
которая принимает значения на интервале
от нуля до
![]() .
.
Тогда точка обрыва,
точка
![]() (то есть случайная величина
(то есть случайная величина
![]() примет значение
примет значение
![]() ),
не может являться вероятностной
характеристикой произошедшего обрыва:
вероятность
),
не может являться вероятностной
характеристикой произошедшего обрыва:
вероятность
![]() .
На самом деле, по геометрической
вероятности:
.
На самом деле, по геометрической
вероятности:
![]() ,
,
где
![]() - длина точки
- длина точки
![]() ,
,
![]() - расстояние
между пунктами
- расстояние
между пунктами
![]() и
и
![]() .
Но
.
Но
![]() !
Как охарактеризовать с вероятностной
точки зрения линию обрыва?
!
Как охарактеризовать с вероятностной
точки зрения линию обрыва?
Непрерывную
случайную величину
![]() характеризуют с помощью функции
распределения.
характеризуют с помощью функции
распределения.
Функцией
распределения
случайной величины
![]() называется функция
называется функция
![]() ,
выражающая для каждого числа
,
выражающая для каждого числа
![]() вероятность того, что случайная величина
вероятность того, что случайная величина
![]() примет какое-либо значение, меньшее
числа
примет какое-либо значение, меньшее
числа
![]() :
:
![]() .
.
Функция распределения
определена для всех
![]() :
:
![]() ,
а значения
,
а значения
![]() принимает на отрезке
принимает на отрезке
![]() ,
т.к. вероятность любого события находится
именно в этих пределах.
,
т.к. вероятность любого события находится
именно в этих пределах.
Функцией распределения можно характеризовать (в равной степени) и дискретные случайные величины.
_______________
Пример.
Пусть
![]() - число попаданий в цель при четырех
выстрелах, если вероятность попадания
при одном выстреле равна
- число попаданий в цель при четырех
выстрелах, если вероятность попадания
при одном выстреле равна
![]() (пример из предыдущей лекции). Найти и
изобразить функцию распределения этой
случайной величины
(пример из предыдущей лекции). Найти и
изобразить функцию распределения этой
случайной величины
![]() .
.
Решение.
В предыдущей лекции мы нашли, что закон
распределения
![]() имеет вид:
имеет вид:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдём функцию
распределения
![]() .
При значении
.
При значении
![]() функция
функция
![]() ,
т.к. событие
,
т.к. событие
![]() можно составить из пяти несовместных
событий:
можно составить из пяти несовместных
событий:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
вероятности которых
в сумме дают
![]() .
И это справедливо для всех
.
И это справедливо для всех
![]() ,
таких, что
,
таких, что
![]() .
Поэтому
.
Поэтому
![]() при значении
при значении
![]() .
.
Но как только
![]() принимает значение
принимает значение
![]() ,
сразу из перечисленного выше множества
событий исключается событие
,
сразу из перечисленного выше множества
событий исключается событие
![]() (т.к.
(т.к.
![]() ). Поэтому:
). Поэтому:
![]()
![]() .
.
И так будет для
всех
![]() ,
таких что
,
таких что
![]() .
Поэтому
.
Поэтому
![]() для всех
для всех
![]() ,
таких что
,
таких что
![]() .
.
И так далее.… До
значения
![]() ,
которому не соответствует ни одно из
событий
,
которому не соответствует ни одно из
событий
![]() (т.е. переменная
(т.е. переменная
![]() принимает значения от
принимает значения от
![]() до
до
![]() с шагом равным
с шагом равным
![]() ).
Поэтому для всех значений
).
Поэтому для всех значений
![]() ,
таких, что
,
таких, что
![]() ,
значение функции распределения равно
,
значение функции распределения равно
![]() .
.
Итак, для рассматриваемой здесь случайной величины функция распределения имеет вид:

Графиком функции
распределения
![]() является «набор из горизонтальной линии
является «набор из горизонтальной линии
![]() и горизонтальных стрелок» рис. 6.1, которые
говорят о том, что предел справа у функции
не достигается в пяти случаях:
и горизонтальных стрелок» рис. 6.1, которые
говорят о том, что предел справа у функции
не достигается в пяти случаях:
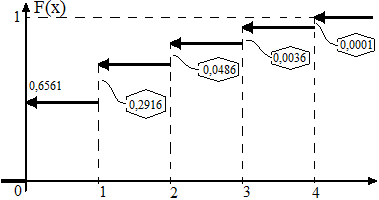
Рис. 6.1. Функция распределения дискретной случайной величины.
