1.3 Властивості відношень

1. PART OF і SUP володіють властивістю транзитивності:

Якщо ₁ SUP ₂ та ₂ SUP ₃ то ₁ SUP ₃

Рисунок 1.11

Наприклад, Якщо «доцент SUP викладач» і «викладач SUP співробітник» то «доцент SUP співробітник» (рис.1.11).

2. Для відношення INS ця властивість не виконується:

Якщо ₁ INS ₂; ₂ INS ₃; …; _n-1 INS _n невірно, що _n INS ₁.

В графі відношення INS немає циклів

3. Якщо ₁ SUP ₂; ₂ INS ₃ то ₁ INS ₃

Наприклад, якщо «лаборант SUP співробітник лабораторії»; «співробітник лабораторії INS лабораторія» то «лаборант INS лабораторія»

Рисунок 1.12

4. Якщо name (O) ISA ₁; ₁ SUP ₂ то name (O) ISA ₂

Наприклад, «Івано-Франківськ ISA місто» ; «місто SUP населений пункт» «Івано-Франківськ ISA населений пункт»

Представлення типів об'єктів

Кінцева множина трійок вигляду (, n_i, _i) називається представленням типу , якщо в кожен момент часу n_i: _об^t  (_i)_об^t (n_i – відображення множини об'єктів типу  на множину об'єктів типу ₁), причому різним об'єктам О₁ і О₂ типу  відповідають різні ккортежі значень функцій n_i:

{n₁^t(O₁), n₂^t(O₁),..., n_k^t(O₁)}

{n₁^t(O₂), n₂^t(O₂),..., n_k^t(O₂)},

остання умова називається умовою розрізнюваності об'єктів.

де, _і – типи об'єктів,

n_i – ім'я атрибуту (атрибути – характеристики об'єктів або ролі, які вони грають в певних ситуаціях);

i=1..., k;

n_in_j, якщо ij,

Як приклад розглянемо об'єкт типу автомобіль (, n_i, _i)

(автомобіль, марка, марка автомобіля)

(автомобіль, номер, номер автомобіля)

(автомобіль, колір, колір автомобіля)

автомобіль(Таврія, АТ4554АК, білий)

автомобіль(Ланос, АТ2222АН, червоний)

1.4 Композиційний тип об'єктів

(n_i, _i) COMPONENT OF 

COMPONENT OF означає, що об'єкт типу _i є компонентой об'єкту типу .

Рисунок 1.13

Приклад композиційного об'єкту, ситуація «знаходиться» ( людина знаходиться в певному приміщенні в певний час)

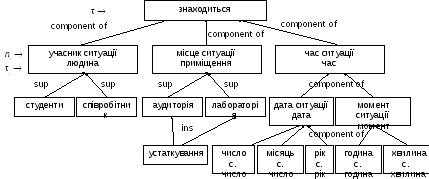
Рисунок 1.14

На основі рис. 1.14 можна формувати шаблонні вислови, наприклад:

людина . . . знаходиться в приміщенні . . . у час . . .

співробітник . . . знаходиться в аудиторії . . . у . . . год. . . . хвилин . . .

. . . число . . . місяць . . . рік

У шаблонні вислови можуть бути поставлені імена конкретних об'єктів.

1.5. Мінімальне уявлення

Уявлення {(, n_i, _i) i=1...k} називають мінімальним, якщо при видаленні  з цих трійок, множина трійок, що залишилася, перестає бути представленням даного типу об'єктів.

Приклад:

 - оренда:

₁ - об'єкт оренди

₂ - орендатор

₃ - орендодавець

₄ - термін оренди

₅ - вартість оренди

1.6. Функціональна залежність

Припустимо, задано уявлення

{(, n_i, _i) i=1...k}

X = {_i1, ..., _ip}

Y = {_j1, ..., _js}

Говорять, що компоненти Y функціонально залежать від компонент X, якщо в будь-який момент часу t для будь-яких двох об'єктів О₁, О₂  _обt з рівності:

n_i1^t(O₁) = n_i1^t(O₂)

. . .

n_ip^t(O₁) = n_ip^t(O₂),

слідують рівності:

n_j1^t(O₁) = n_j1^t(O₂)

. . .

n_js^t(O₁) = n_js^t(O₂)

Наприклад: X = {_4, _5, ₆}, Y = {_1, _2,₃}


Лекція
лектор	слухач	предмет лекції	місце	день тижня	час початку
викладач	група	предмет	аудиторія	дата
1	2	3	4	5	6

Рисунок 1.15