6. Пример выполнения

В трубопроводе (рисунок 6) необходимо вытеснить затор массой m, движущейся со скоростью V₀ . При этом известны силовые параметры.

Дано:

m = 4 кг

V₀ = 12, м/с

Q = 12, Н

R = 0,8V², Н

l = 2,5, м

f = 0,2

F_x =- 8cos(4t), Н

Рисунок 6

Определить: скорость подхода затора D на участке АВ в точке В и

закон движения затора x = f(t) на участке BC.

Решение

Модель движения затора D представлена на рисунке 6. Из точки А под действием принудительной силы сдвинули условную точку D в начальный момент времени массой m = 4кг, со скоростью V₀ = 12 м/с, ГД в точке А установлена декартова система координат Axyz. Противодавление равно

Q = 12 Н, сила сопротивления R = 0,8V² . Длина участков АВ и ВС одинакова и равна L = 2,5 м. На втором участке действует сила трения с коэффициентом трения f = 0,2 .

1. Движение тела на участке ав Силы, действующие на этом участке на тело d показаны на рисунке. Зададим ось ох и запишем основное уравнение динамики движения груза :

.

Необходимо преобразовать в левой части уравнения переменные. Домножим и разделим на dx

,

Подставив в правой части значение R, имеем

.

Разделим левую и правую части уравнения на массу m

.

Сделав соответствующие преобразования, имеем

, ; ,

, , , получим

.

По начальным условиям при t = 0, х = 0; V = V₀, откуда постоянная интегрирования. В результате преобразования находим

,

,

, ,

, в результате

извлечения корня получим значение скорости м/с.

Примечание. Закон изменения скорости на участке АВ и закон движения объекта D

на участке ВС в функции от времени изобразить графики с

применением программы MATHCAD или Avanced Grapher.

2. Движение тела на участке вс

Уравнение движения в проекции на ось х будет иметь следующий вид:

. Положение тела D показано на рисунке 7.

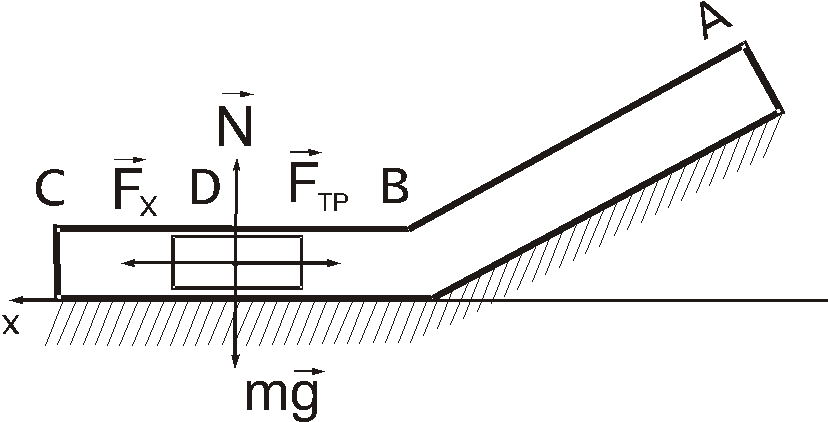
Рисунок 7

Рассмотрим правую часть уравнения. Разделим поэтапно на массу и представим в виде ; . Тогда уравнение движения преобразуется к виду . Интегрируем это уравнение . Находим постоянные из начальных условий :

при t = 0; V = V₀ = V_B =5,6 следует, что тогда проекция скорости на ось х изменяется по закону

.

Закон движения тела определяем как умножая на dt и интегрируя, получим

При x = 0 и t = 0 вычисляем постоянную интегрирования и уравнение принимает следующий вид .

Поскольку первым и последним слагаемым можно пренебречь, то закон движения тела D запишем как .

13