
- •Методические указания к выполнению расчетно-графического задания по теме «Векторный анализ. Элементы теории векторного поля»
- •Оглавление
- •Введение
- •Методические указания по теме «Векторный анализ. Элементы теории векторного поля»
- •Справочный материал к выполнению ргз
- •1. Криволинейные интегралы II рода (по координатам)
- •1.1. Вычисление криволинейного интеграла II рода и его механическая трактовка.
- •1.2. Условие независимости криволинейного интеграла II рода от формы пути интегрирования.
- •2. Векторная функция скалярного аргумента
- •3. Векторное поле
- •3.1. Поток векторного поля через поверхность.
- •3.2. Дивергенция векторного поля.
- •3.3. Формула Остроградского-Гаусса.
- •4. Потенциальные и соленоидальные векторные поля
- •4.1. Ротор векторного поля.
- •4.2. Потенциальное векторное поле и его потенциал.
- •4.3. Соленоидальное векторное поле.
- •Решение примерного варианта ргз
- •Задания ргз по теме «Векторный анализ. Элементы теории векторного поля»
- •Вопросы для самопроверки
- •Рекомендуемая литература
3.3. Формула Остроградского-Гаусса.
Формула Остроградского-Гаусса устанавливает связь между интегралом по замкнутой поверхности σ в направлении ее «внешней» нормали и тройным интегралом по области V, ограниченной этой поверхностью:
![]() .
.
Если
![]() – векторное поле, то векторная запись
формулы Остроградского-Гаусса:
– векторное поле, то векторная запись
формулы Остроградского-Гаусса:
![]() , (9)
, (9)
т.е. поток
вектора
![]() через замкнутую поверхность σ
в направлении ее «внешней» нормали
равен тройному интегралу от
дивергенции
этого поля по области V,
ограниченной этой поверхностью.
через замкнутую поверхность σ
в направлении ее «внешней» нормали
равен тройному интегралу от
дивергенции
этого поля по области V,
ограниченной этой поверхностью.
4. Потенциальные и соленоидальные векторные поля
4.1. Ротор векторного поля.
Ротором
(вихрем) векторного поля
![]() называется вектор
называется вектор
![]() .
.
Ротор – это векторная величина, которая
является дифференциальной характеристикой
векторного поля. Всякое векторное поле
![]() сопровождает другое векторное поле
сопровождает другое векторное поле
![]() его роторов.
его роторов.
Для вычисления ротора удобно использовать его запись в форме определителя:
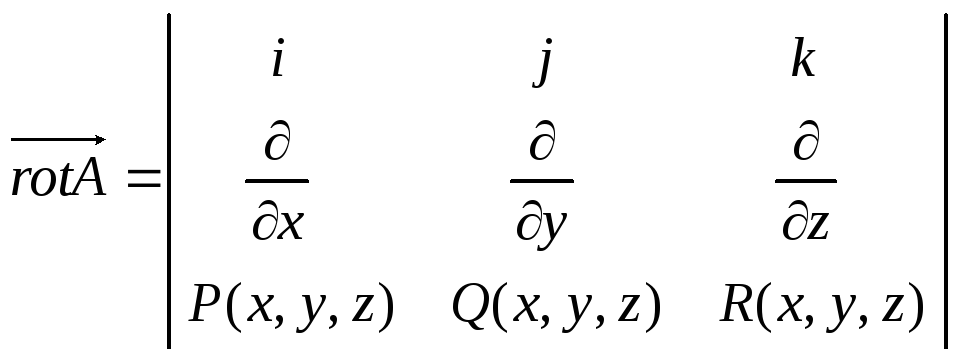 (10)
(10)
где вектор
![]() – это векторно-дифференциальный
оператор, называемый оператором
Гамильтона «набла». При вычислении
определителя умножению координат
соответствует операция дифференцирования:
– это векторно-дифференциальный
оператор, называемый оператором
Гамильтона «набла». При вычислении
определителя умножению координат
соответствует операция дифференцирования:
![]() .
.
4.2. Потенциальное векторное поле и его потенциал.
Векторное поле
![]() называется потенциальным, если
существует такая функция
называется потенциальным, если
существует такая функция
![]() ,
что
,
что
![]() .
Функция U называется
потенциалом векторного поля.
.
Функция U называется
потенциалом векторного поля.
Из определения следует, что потенциальное
векторное поле – это поле градиентов
некоторого скалярного поля
![]() .
.
Признак потенциальности векторного
поля: векторное поле
![]() является потенциальным тогда и только
тогда, когда его ротор – нулевой вектор:
является потенциальным тогда и только
тогда, когда его ротор – нулевой вектор:
![]() . (11)
. (11)
Одно из свойств потенциальных полей
заключается в том, что если .
![]() – потенциальное векторное поле, то его
линейный интеграл по любой кривой
MN, т.е. интеграл вида
– потенциальное векторное поле, то его
линейный интеграл по любой кривой
MN, т.е. интеграл вида
![]()
не зависит от формы кривой MN и равен разности потенциалов в конечной и начальной точках:
![]() . (12)
. (12)
Это свойство можно использовать для нахождения потенциала векторного поля при помощи криволинейного интеграла II рода. Для этого нужно взять фиксированную точку М(x0, y0, z0) и произвольную (текущую) точку N(x, y, z) и вычислить линейный интеграл по пути MN:
![]() . (13)
. (13)
При этом
получаем потенциал векторного поля
![]() с точностью до произвольной постоянной.
с точностью до произвольной постоянной.
После нахождения потенциала векторного
поля его линейный интеграл
![]() для любых заданных точек M
и N можно вычислить
по формуле (12).
для любых заданных точек M
и N можно вычислить
по формуле (12).
4.3. Соленоидальное векторное поле.
Векторное поле
![]() называется соленоидальным, если
существует такое векторное поле
называется соленоидальным, если
существует такое векторное поле
![]() ,
для которого поле
,
для которого поле
![]() является полем роторов:
является полем роторов:
![]() .
.
Поле
![]() называется векторным потенциалом
векторного поля
называется векторным потенциалом
векторного поля
![]() .
.
Признак соленоидальности векторного
поля: векторное поле
![]() является соленоидальным тогда и только
тогда, когда его дивергенция равна нулю:
является соленоидальным тогда и только
тогда, когда его дивергенция равна нулю:
![]() . (14)
. (14)
Решение примерного варианта ргз
Задача
1.
Вычислить работу силы
![]() при перемещении точки приложения силы
вдоль заданной кривой L:
при перемещении точки приложения силы
вдоль заданной кривой L: ![]() от точки B
до точки C,
если значения параметра t
в точках B
и C
заданы:
от точки B
до точки C,
если значения параметра t
в точках B
и C
заданы:
![]() .
.
Решение.
Для
вычисления работы используем криволинейный
интеграл II
рода (формула (3)):
 .
.
Составленный криволинейный интеграл сводим к определенному интегралу, используя параметрические уравнения кривой ВС:
 .
.
Для заданной кривой получаем:

Таким образом, для нахождения работы нужно вычислить определенный интеграл:

Сделаем замену переменной в определенном интеграле:
![]() ,
,
![]() ,
,
тогда
получим:
 .
.
Используем
прием «подведение под знак дифференциала
части подинтегральной функции»:
![]()

![]()
Ответ:
![]() ед. работы.
ед. работы.
Задача 2. Задан радиус-вектор движущейся точки:
![]() .
Найти векторы скорости и ускорения
движения этой точки через 2 минуты после
начала движения.
.
Найти векторы скорости и ускорения
движения этой точки через 2 минуты после
начала движения.
Решение.
Вектор-функция задана в координатной
форме:
![]() .
.
Найдем первые и вторые производные ее проекций x(t), y(t) z(t) по аргументу t:

Найдем векторы скорости и ускорения движения точки по формулам (4) и (5):
![]()
![]() .
.
Через 2 минуты после начала движения векторы скорости и ускорения будут:
![]() ,
,
![]() .
.
Ответы:
![]() ,
,
![]() .
.
Задача
3. Дано
векторное поле
![]() и уравнение плоскости :
3x
+ y
+ 2z
– 3 = 0. Требуется:
и уравнение плоскости :
3x
+ y
+ 2z
– 3 = 0. Требуется:
-
найти поток поля
 через плоскость треугольника АВС
где А,
В,
и С
– точки пересечения плоскости
с координатными осями, в направлении
нормали плоскости, ориентированной
«от начала координат»; построить чертеж
пирамиды ОАВС,
где О
– начало координат;
через плоскость треугольника АВС
где А,
В,
и С
– точки пересечения плоскости
с координатными осями, в направлении
нормали плоскости, ориентированной
«от начала координат»; построить чертеж
пирамиды ОАВС,
где О
– начало координат; -
используя формулу Остроградского-Гаусса, вычислить поток поля
 через полную поверхность пирамиды ОАВС
в направлении
внешней нормали.
через полную поверхность пирамиды ОАВС
в направлении
внешней нормали.
Решение.
-
Чтобы вычислить поток поля
 через плоскость треугольника АВС
используем формулу (6): ПАВС
=
через плоскость треугольника АВС
используем формулу (6): ПАВС
= ,
где D
– проекция
треугольника АВС
на плоскость
xOy,
F
– функция,
задающая плоскость ,
которой принадлежит треугольник АВС.
,
где D
– проекция
треугольника АВС
на плоскость
xOy,
F
– функция,
задающая плоскость ,
которой принадлежит треугольник АВС.
Д ля
построения чертежа найдем точки А,
В,
и С
пересечения плоскости
с координатными осями:
ля
построения чертежа найдем точки А,
В,
и С
пересечения плоскости
с координатными осями:


 .
.
Построим чертеж пирамиды, отложив на координатных осях точки А, В, С и соединив их с началом координат O (рис. 9).
Из
уравнения плоскости :
3x
+ y
+ 2z
– 3 = 0, которое имеет вид F(x, y, z)
= 0, находим
![]() .
.
Поскольку
все три проекции градиента положительные,
то этот вектор образует с координатными
осями острые углы, т.е. направлен «от
начала координат» по отношению к
плоскости .
Это означает, что вектор
![]() и орт «внешней» нормали
и орт «внешней» нормали
![]() ,
указанный в задаче, совпадают по
направлению, поэтому вычисление потока
через плоскость треугольника АВС
сводится к вычислению двойного интеграла:
ПАВС
= +
,
указанный в задаче, совпадают по
направлению, поэтому вычисление потока
через плоскость треугольника АВС
сводится к вычислению двойного интеграла:
ПАВС
= + (перед интегралом ставим знак «+»), где
AOВ
– проекция
треугольника ABC
на плоскость
xOy.
(перед интегралом ставим знак «+»), где
AOВ
– проекция
треугольника ABC
на плоскость
xOy.
Для расстановки пределов интегрирования по треугольнику AOВ (рис. 10) найдем уравнение прямой АВ на плоскости xOy:


 Вычислим
Вычислим
![]() и получим подинтегральную функцию,
подставив
и получим подинтегральную функцию,
подставив
![]() =
2 и
=
2 и
![]() (из уравнения плоскости):
(из уравнения плоскости):
 .
.
Таким
образом, поток поля
![]() через плоскость треугольника АВС:
через плоскость треугольника АВС:
![]() .
.
Вычислим внутренний интеграл по переменной y:

Вычислим внешний интеграл по переменной х:
 .
.
2)
Чтобы вычислить поток поля
![]() через полную поверхность пирамиды ОАВС,
воспользуемся формулой Остроградского-Гаусса:
через полную поверхность пирамиды ОАВС,
воспользуемся формулой Остроградского-Гаусса:
![]() .
.
Найдем
дивергенцию
этого поля по
формуле (8):
![]() .
Для поля
.
Для поля
![]() получаем:
получаем:
![]() .
.
Вычислим
поток поля
![]() через полную поверхность пирамиды ОАВС:
через полную поверхность пирамиды ОАВС:
![]() ,
где
,
где
![]() – объем пирамиды ОАВС.
Этот объем можно вычислить, следующим
образом:
– объем пирамиды ОАВС.
Этот объем можно вычислить, следующим
образом:
![]() .
.
В
результате получаем:
![]() .
.
Ответы: ПABC = 8,5, рисунок 9; 2) ПОАВС = –2,25.
Задача
4. Проверить,
является ли векторное поле силы
![]() потенциальным или соленоидальным. В
случае потенциальности поля найти его
потенциал и вычислить с помощью потенциала
работу силы
потенциальным или соленоидальным. В
случае потенциальности поля найти его
потенциал и вычислить с помощью потенциала
работу силы
![]() при перемещении единичной массы из
точки M(0,1,0)
в точку
N(–1,2,3).
при перемещении единичной массы из
точки M(0,1,0)
в точку
N(–1,2,3).
Решение.
Для
проверки потенциальности векторного
поля
![]() найдем его ротор по формуле (10):
найдем его ротор по формуле (10):

Следовательно, поле потенциально.
Для проверки соленоидальности поля найдем его дивергенцию по формуле (8):
![]() .
.
Следовательно, поле не соленоидально.
Для нахождения потенциала U(x, y, z)
векторного поля возьмем фиксированную
точку В(0, 0, 0), текущую
точку С(x, y, z) и
вычислим криволинейный интеграл
![]() по ломаной ВEKC,
звенья которой параллельны осям координат
и E(x, 0, 0),
K(x, y, 0)
(см. рис. 7). По формуле (12)
получим:
по ломаной ВEKC,
звенья которой параллельны осям координат
и E(x, 0, 0),
K(x, y, 0)
(см. рис. 7). По формуле (12)
получим:

Получили
потенциал поля
![]() ,
где С –
произвольная постоянная. Для проверки
решения найдем градиент потенциала
,
где С –
произвольная постоянная. Для проверки
решения найдем градиент потенциала
![]() :
:
![]() .
Следовательно, потенциал поля силы
найден верно.
.
Следовательно, потенциал поля силы
найден верно.
Найдем
работу векторного поля
![]() при перемещении единичной массы из
точки M(0,1,0)
в точку
N(–1,2,3)
по формуле (11):
при перемещении единичной массы из
точки M(0,1,0)
в точку
N(–1,2,3)
по формуле (11):
 .
.
Ответы:
поле
![]() потенциально, не соленоидально;
потенциально, не соленоидально;
![]() ,
где С –
произвольная постоянная; работа А
= –10.
,
где С –
произвольная постоянная; работа А
= –10.
