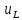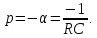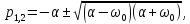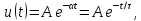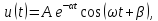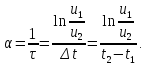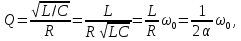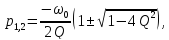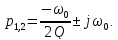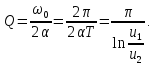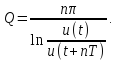Завьялов лабы / 3

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

КафедраТОЭ

отчет

по лабораторной работе № 3 по дисциплине

«Теоретические основы электротехники»

Тема: Исследование свободных процессов

в электрических цепях

Студент гр. 6307		Лазарев С.О.
Преподаватель		Завьялов А.Е.

Санкт-Петербург

2018

Цель работы

Изучение связи между видом свободного процесса в электрической цепи и расположением ее собственных частот (корней характеристического уравнения) на комплексной плоскости; экспериментальное определение собственных частот и добротности RLC-контура по осциллограммам.

Основные теоретические положения

В работе изучаются свободные процессы в цепях, схемы которых представлены на рисунке 1. Цепи возбуждаются очень короткими импульсами тока 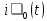, заряжающими емкость 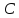. В паузах между импульсами емкость разряжается, и цепь находится в свободном режиме, т.к. в это время источник возбуждения отключен: .

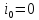В линейных цепях свободный процесс описывается линейными дифференциальными уравнениями, и его вид определяется корнями характеристического уравнения (собственными частотами цепи ).

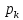+ а) б)

При возбуждении цепи источником тока собственные частоты можно рассчитать как нули входной проводимости :

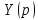1. для цепи первого порядка, изображенной на рис. 1, а),

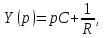
откуда получим

2. для цепи второго порядка, изображенной на рис. 2, б),

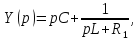
откуда

где

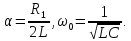
Общий вид решения для напряжения любого элемента цепи

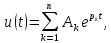
где 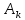— постоянные интегрирования, 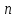— порядок цепи.

У цепи первого порядка одна собственная частота (1), вещественная и отрицательная, свободный процесс имеет вид

процесс экспоненциальный, причем 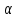— постоянная затухания, а 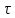— постоянная времени экспоненты. Временная диаграмма свободного процесса показана на рис. 2, а), причем 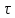— интервал времени, соответствующий любой подкасательной к экспоненте.

В цепи второго порядка две собственные частоты (2) могут быть вещественными (апериодический режим; временная диаграмма суммы двух экспонент, изображенных пунктиром, показана на рис. 2, б) или комплексно-сопряженными. Комплексно-сопряженным частотам соответствует качественно новый характер свободного процесса — колебательный:

где 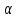— постоянная затухания, 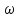— частота затухающих колебаний. Временная диаграмма колебательного процесса представлена на рис. 2, в).

В цепи второго порядка возможен также критический режим (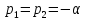, кратные собственные частоты); вид процесса 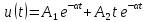близок к диаграмме, показанной на рис. 2, б), причем момент достижения максимума , если .

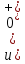а) б) в)

В некоторых случаях собственные частоты относительно просто рассчитываются по осциллограммам. Например, согласно (3), по рис. 2, а) можно рассчитать постоянную затухания:

В случае 2, в) постоянная затухания также может быть определена на основании (5), но при этом обязательно выполнение условия 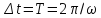, что вытекает из (4).

Особый интерес представляет определение добротности RLC-контуров по виду свободного процесса. Для последовательного RLC-контура справедлива формула

где 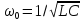— частота незатухающих колебаний в идеальном контуре (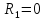). Согласно (2) собственные частоты последовательного RLC-контура можно записать в виде

причем 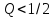соответствует апериодический режим, 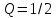— критический, 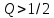— колебательный, а 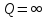— незатухающий колебательный.

При 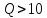с высокой степенью точности можно считать

С учетом (6) формула, позволяющая в данном случае определить добротность по осциллограмме 2, в), имеет вид

Для повышения точности можно брать отношение напряжений за 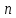периодов колебаний:

Замечание. Собственные частоты цепей можно было рассчитать и, например, с использованием уравнений состояния. Так, для цепи, изображенной на рис. 1, б), составим такие уравнения Кирхгофа:

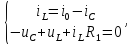
откуда очевидным образом следует система дифференциальных уравнений

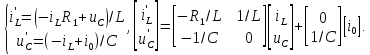
Характеристическое уравнение имеет вид 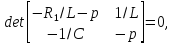или, что то же самое, 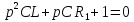. Его корни равны

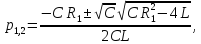
этот результат с точностью до обозначений совпадает с (2).

Экспериментальные результаты

Исследование свободных процессов в цепи первого порядка

С = 0,02 мкФ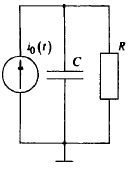

R = 5 кОм

Рис. 1. Исследуемая цепь

Рассчитаем теоретическое значение корня характеристического многочлена p₁=

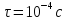
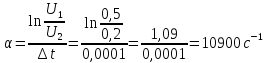
Найдем частоту:

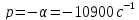
Вопрос 1. Каким аналитическим выражением описывается осциллографируемый процесс?

Данный процесс описывается затухающей экспонентой с постоянным коэффициентом. Так как процесс свободный, то вынужденной составляющей нет. По осциллограмме можно определить 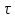как 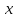– координату точки пересечения касательной к осциллограмме в начальной точке с осью абсцисс.

Вопрос 2. Соответствует ли найденная собственная частота теоретическому расчету?

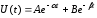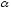Общий вид выражения для исследованных процессов: , где и 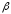могут быть и комплексными (колебательный случай). Собственные частоты цепи, которая соответствует первой осциллограмме, можно определить, исходя из формулы:

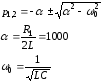
также можно найти на основе осциллограммы как отношение логарифма к отношению значений напряжений 2-х соседних максимумов и временной разности (периода) между этими 2-мя максимума

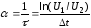
Исследование свободных процессов в цепи второго порядка

С = 0,02 мкФ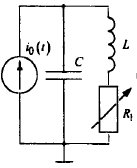

Рис. 2. Исследуемая цепь

L = 25 мГн

Апериодический режим (R₁ = 0,5 кОм):

Собственная частота:

• Теоретическое значение:

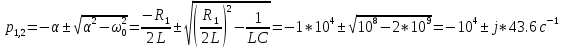
• Практическое значение:

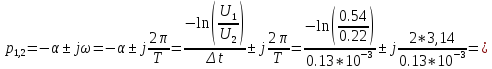
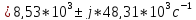
Добротность:

Теоретическая:

Практическая:

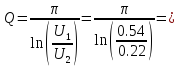2,83

Апериодический режим (R₁ = 3 кОм):

Рассчитаем теоретическое значение собственных частот:

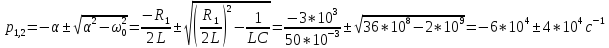
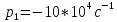
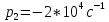
Критический режим (R₁ = 1,5 кОм):

Собственная частота:

Практическое значение:

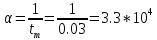
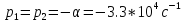
Теоретическое значение:

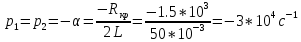
(R₁ = 0 кОм):

Добротность:

Практическая:

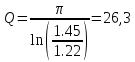
Вопрос 3. Каким аналитическим выражением (в общем виде) описываются процессы во всех четырех случаях?

+

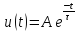
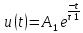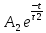
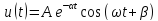
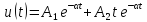
Вопрос 4. Соответствуют ли найденные собственные частоты теоретическому расчету?

Соответствуют т.к. в колебательном и критическом режимах они совпадают, а в остальных исследованиях вид собственных частот соответствует теоретическому, а именно при сопротивлении R₁ =3 кОм обе собственных частоты имеют вещественный вид.

Вопрос 5. Каковы теоретические значения собственных частот при

R₁ = 3 кОм и соответствует ли это значениям снятая осциллограмма?

Значения собственных частот:

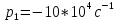
Они соответствуют снятой осциллограмме, т.к. они вещественны и различны, а значит, выходной сигнал должен быть непериодическим, что и видно по осциллограмме.

Вопрос 6. Как соотносятся найденные значения добротности с результатами теоретического расчета?

Практическая добротность равна 26,3, а теоретическая в свою очередь в идеальном контуре равна бесконечности (α = 0). Из этого следует, что качество элементов контура не идеально и их характеристики сильно влияют на добротность.

Исследование свободных процессов в цепи третьего порядка

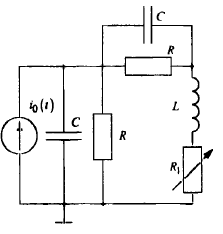
С = 0,02 мкФ

R =5 кОм

R₁ = 1 кОм

L = 25 мГн

Рис. 3. Исследуемая цепь

Рассчитаем собственные частоты:

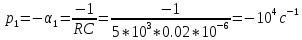
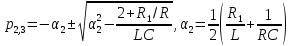
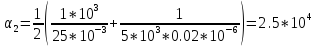
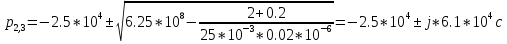
Вопрос 7. Каким выражением описывается осциллографируемый процесс?

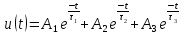
Вопрос 8. Каковы значения собственных частот, найденных при помощи теоретического расчета и соответствует ли этим значениям снятая осциллограмма?

Значения собственных частот:

, .

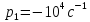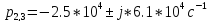Снятая осциллограмма соответствует данным собственным частотам, потому что на ней виден периодический процесс, что соответствует частотам 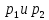и так же виден изгиб экспоненты, что соответствует собственной частоте .

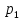Вывод

Форма реакции цепи зависит от вида собственных частот: если собственные частоты вещественные — апериодический режим, комплексно-сопряженные — периодический режим, кратные — критический апериодический режим.Так как изучались не идеальные, а реальные цепи результаты аналитических расчетов не совпадают с данными осциллограмм. При аналитических расчетах не учитывались сопротивления проводов, паразитные емкости и индуктивности. Несовпадение теоретических и экспериментальных данных вызвано также неточностью измерений и неточностью номиналов элементов.