46.Дайте определение обобщенных координат механической системы. Каковы их обозначения?

Независимые между собой параметры, которые однозначно определяют положение механической системы в пространстве в любой момент времени, называются обобщенными координатами.

, , s - число уравнений связей; N – кол-во мат. точек в мех. системе.

47.Дайте определение действительного и возможного перемещения точки. Каковы их обозначения?

Действительное перемещение:

Действительным перемещением точки за время dt называется такое элементарное перемещение, которое она фактически совершает в пространстве за время dt при данных связях.

Вектор называется действительным элементарным перемещением точки.

Возможное перемещение:

Возможным называется любое допускаемое связями перемещение материальной точки из положения, занимаемого ею в данный момент времени, в бесконечно близкое положение, которое она может занимать в тот же момент времени.

Вектор называют вариацией радиус-вектора точки, а проекции на оси декартовой системы координат –

вариациями координат. Их обозначают , , .

48.Дайте определение и запишите формулу возможной работы силы. Какие связи называются идеальными?

Возможной работой силы называется работа силы на любом возможном перемещении точки ее приложения: .

Связи называются идеальными, если возможная работа реакций связей на любом возможном перемещении системы из любого ее положения равна нулю: .

49.Сформулируйте определение обобщенной силы.

Обобщенной силой, соответствующей некоторой обобщенной координате, называется скалярная величина, равная коэффициенту при вариации этой обобщенной координаты в выражении возможной работы всех активных сил, действующих на механическую систему.

50.Сформулируйте и запишите принцип возможных перемещений для механической системы.

Для равновесия механической системы, на которую наложены голономные, стационарные, удерживающие и идеальные связи, необходимо и достаточно, чтобы сумма работ всех активных сил, приложенных к точкам системы, на любом возможном перемещении системы равнялась нулю.

51.Как формулируются условия равновесия механической системы в обобщенных координатах.

Для равновесия механической системы с голономными, удерживающими, стационарными и идеальными связями необходимо и достаточно, чтобы все обобщенные силы, соответствующие выбранным обобщенным координатам, равнялись нулю.

52.Сформулируйте и запишите общее уравнение динамики в векторной и аналитической формах.

При любом движении механической системы с идеальными и удерживающими связями в каждый данный момент сумма возможных работ всех активных сил и сил инерции на любом возможном перемещении равна нулю.

;

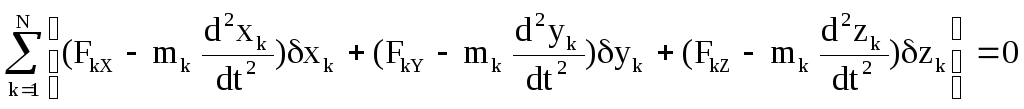
53.Запишите уравнения Лагранжа II рода. Сколько этих уравнений можно составить для конкретной механической системы.

, ()

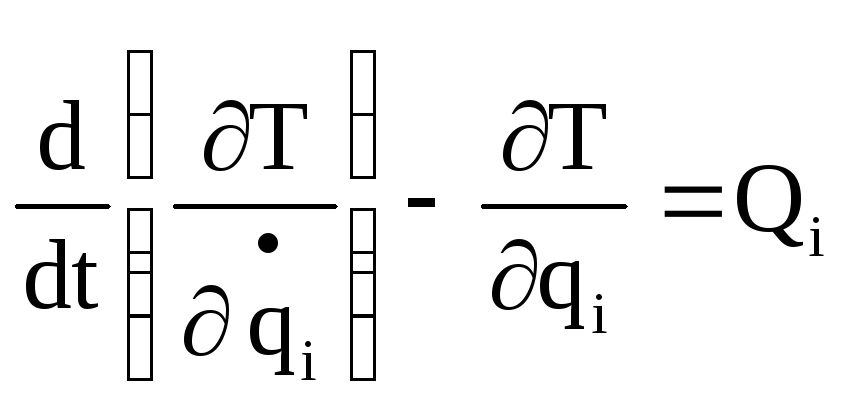3N - число координат у N точек системы в пространстве. s - количество связей, наложенных на систему.

n=3N-s - число обобщенных координат определяющих положение системы (если связи голономные и удерживающие, то n - количество степеней свободы данной системы).

Уравнений для конкретной механической системы

составляют ровно столько, сколько степеней свободы имеет рассматриваемая механическая система, то есть n уравнений.

54.Запишите формулы для кинетической и потенциальной энергии механической системы с одной степенью свободы при малых отклонениях от положения устойчивого равновесия.

«а» называется коэффициентом инерции. - квадрат обобщенной скорости.

«с» - обобщенный коэффициент жесткости. - квадрат обобщенной координаты.

55.Запишите дифференциальное уравнение малых колебаний системы с одной степенью свободы.

, где: = const, круговая или циклическая частота ().

56.Запишите приближенную формулу для диссипативной функции механической системы с одной степенью свободы при малых отклонениях от положения устойчивого равновесия.

«b» - обобщенный коэффициент сопротивления. - квадрат обобщенной скорости.

57.В чем состоит физический смысл диссипативной функции. Запишите соответствующую формулу.

При отсутствии внешнего возмущения, удвоенное значение диссипативной функции равно скорости убывания полной механической энергии системы.

58.Запишите дифференциальное уравнение малых движений системы с одной степенью свободы с учетом сил сопротивления.

, где: = const, круговая или циклическая частота, = const, коэффициент

затухания. Размерности у «n» и «k» одинаковые ().

59.Запишите дифференциальное уравнение вынужденных колебаний системы с одной степенью свободы без учета сопротивления.

, где: = const, круговая или циклическая частота, = const, H - амплитуда обобщенной силы, характ. внешнее воздействие на колебательную систему, p - циклическая (круговая) частота, - начальная фаза обобщенной силы.

60.Дайте определение коэффициента восстановления. По какой формуле можно определить этот коэффициент опытным путем.

При прямом ударе шара о неподвижную поверхность величина, равная отношению абсолютных величин скорости в конце удара к скорости в начале удара, наз. коэфф. восстановления: .

Шарик из испытуемого материала отпускается без нач. скорости с высоты на неподвижную плиту, изготовленную из того же материала. После удара шарик поднимается на высоту . Скорость шарика в начале удара и в конце удара опр. по ф-ле Галилея: и . Подставим значения скоростей в . Получим: .