Тема 13

П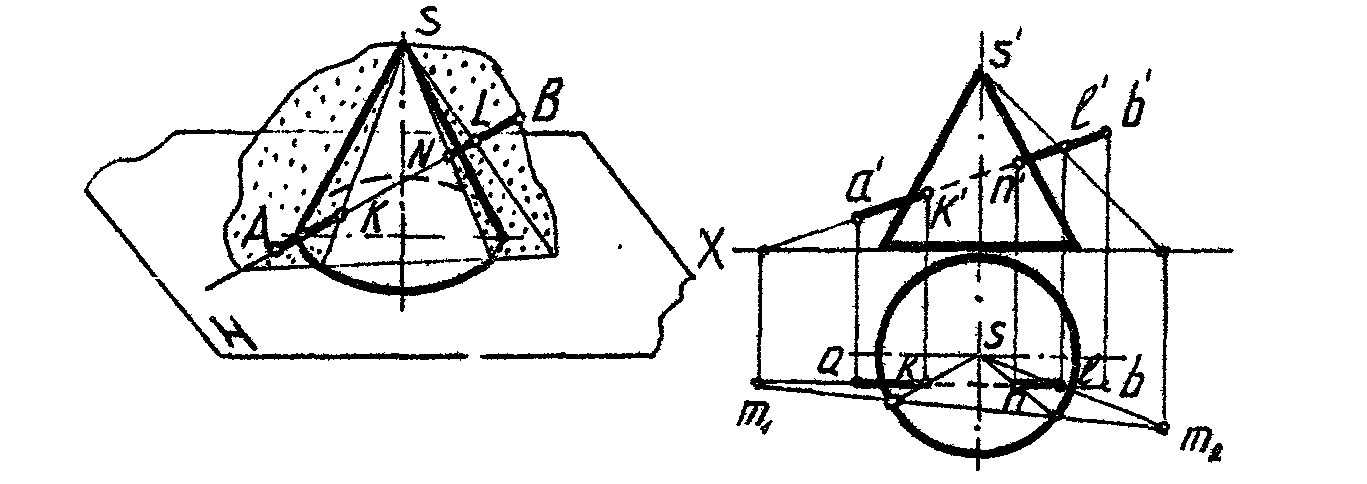 ЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С ПОВЕРХНОСТЬЮ

Пересечение прямой с поверхностью конуса

Для определения точек пересечения прямой с поверхностью тела прямую заключают во вспомогательную плоскость, строят линию пересечения поверхности тела этой плоскостью и отмечают точки пересечения найденной линии с данной прямой. Это искомые точки.

Когда прямая пересекает многогранник или сферу, в качестве вспомогательной применяют проецирующую плоскость. Если задан конус или наклонный цилиндр, прямую заключают во вспомогательную плоскость общего положения, которая рассечет поверхность тела по прямолинейным образующим.

Ч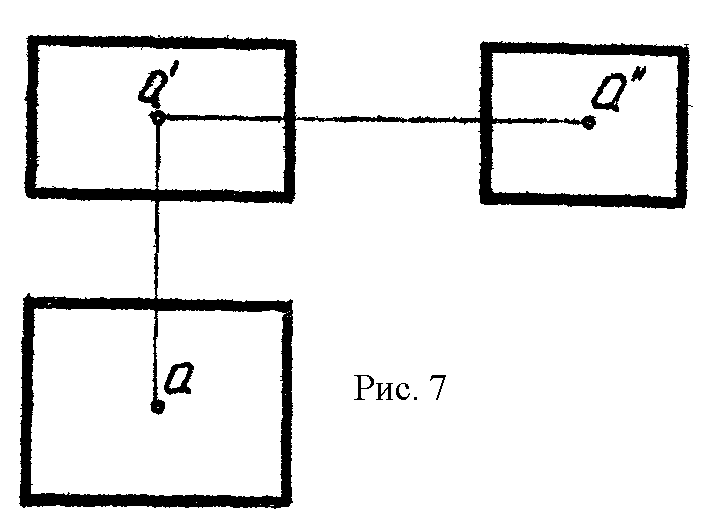 тобы вспомогательная плоскость рассекла поверхность цилиндра по образующим, она должна включать в себя прямую, параллельную образующим цилиндра. Чтобы вспомогательная плоскость рассекла поверхность конуса по образующим, она должна включать прямую, проходящую через вершину конуса. Образующие сечения на поверхности конуса и цилиндра проходят через точки пересечения кривой основания тела со следом вспомогательной секущей плоскости.

Литература: [1, с. 210-211, 115-117]; [2. с. 189-192].

8* Заданы точки А, В, С. и D. Построить:

а) точку Е, расположенную над точкой А , взяв АЕ = 15мм;

б) точку F , расположенную под точкой В , взяв BF = 20 мм;

в) точку M , расположенную за точкой С, взяв СМ =10 мм;

г) точку К , расположенную перед точкой D , взяв ОК=5мм (рис. 6).

9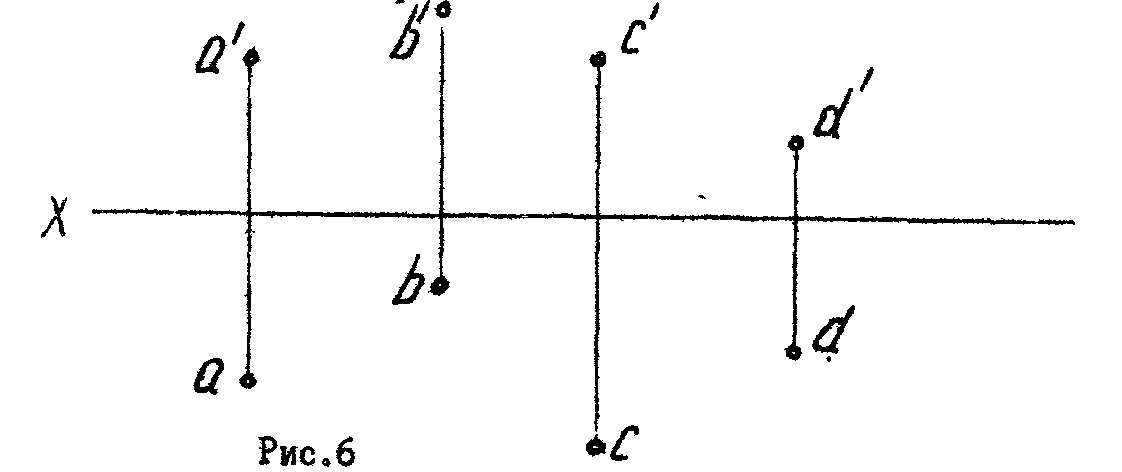 . Дан параллелепипед с точкой А внутри. Построить:

а) точку В, симметричную точке А .относительно верхней грани параллелепипеда;

б) точку С , симметричную точке А относительно передней грани;

в) точку D , симметричную точке А относительно правого верхнего ребра;

г) точку Е , симметричную точке А относительно верхнего переднего ребра;

д) точку F, симметричную точке А относительно нижней передней правой вершины ( рис.7).

4.* Построить в трех проекциях точку В на расстоянии 30 мм от плоскости Н, 40 мм от плоскости V и 50 мм от плоскости W.

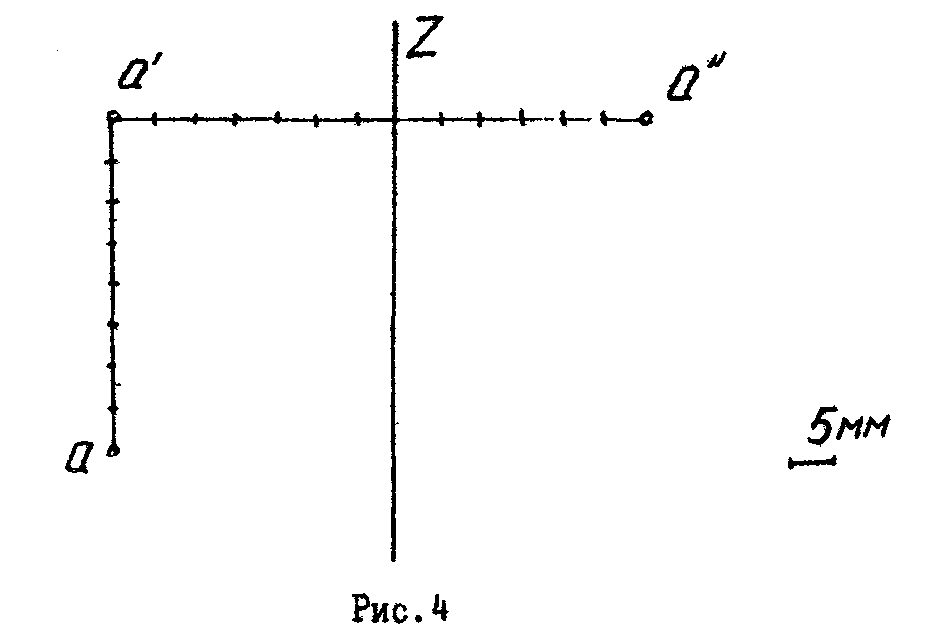
5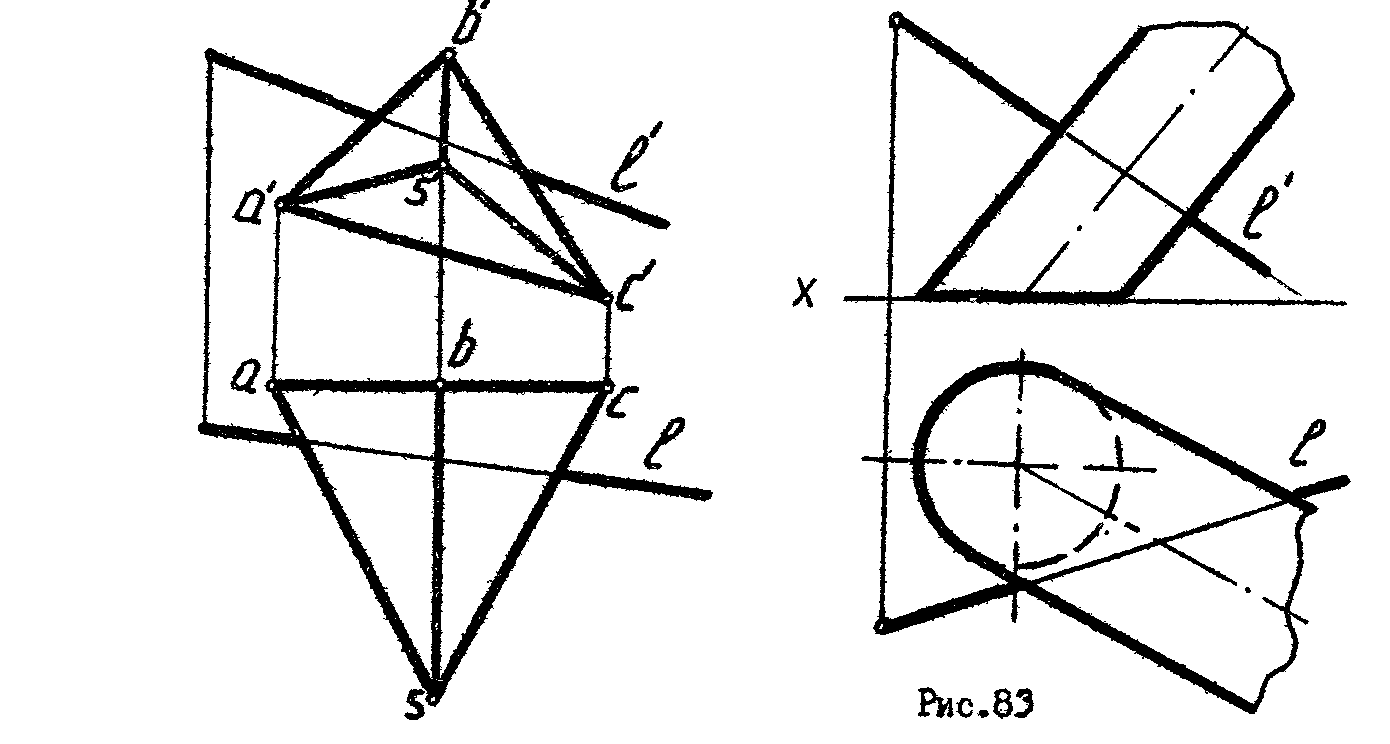 . Даны три проекции точки А . Определить положение осей Х и У и расстояние от точки А в пространстве до плоскостей проекций (рис.4).

6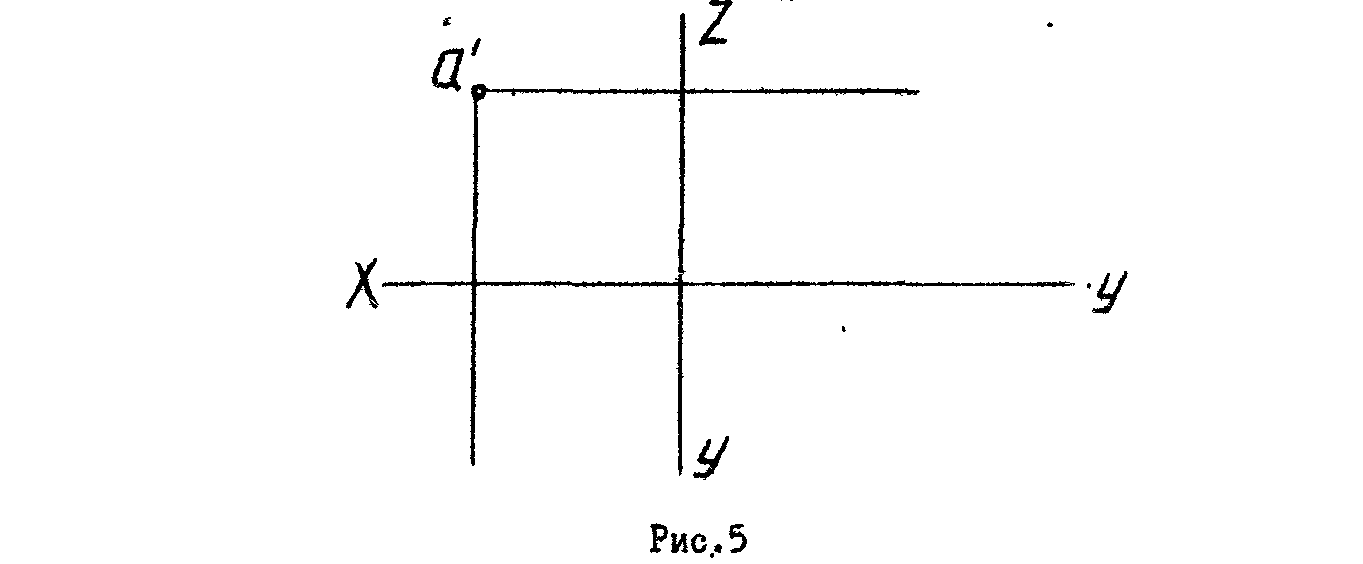 . По фронтальной проекции точки А построить горизонтальную и профильную проекции так, чтобы Z_А=2У_А (рис.5).

7.Точка В симметрична точке А (-20,25) относительно оси Х. Определить расположение точки В и записать ее координаты в системе 2-х плоскостей проекций.

1. Построить проекции точек пересечения прямой с поверхностью многогранника (рис.82).

2. Определить точки пересечения прямой с поверхностью цилиндра (рис.83).

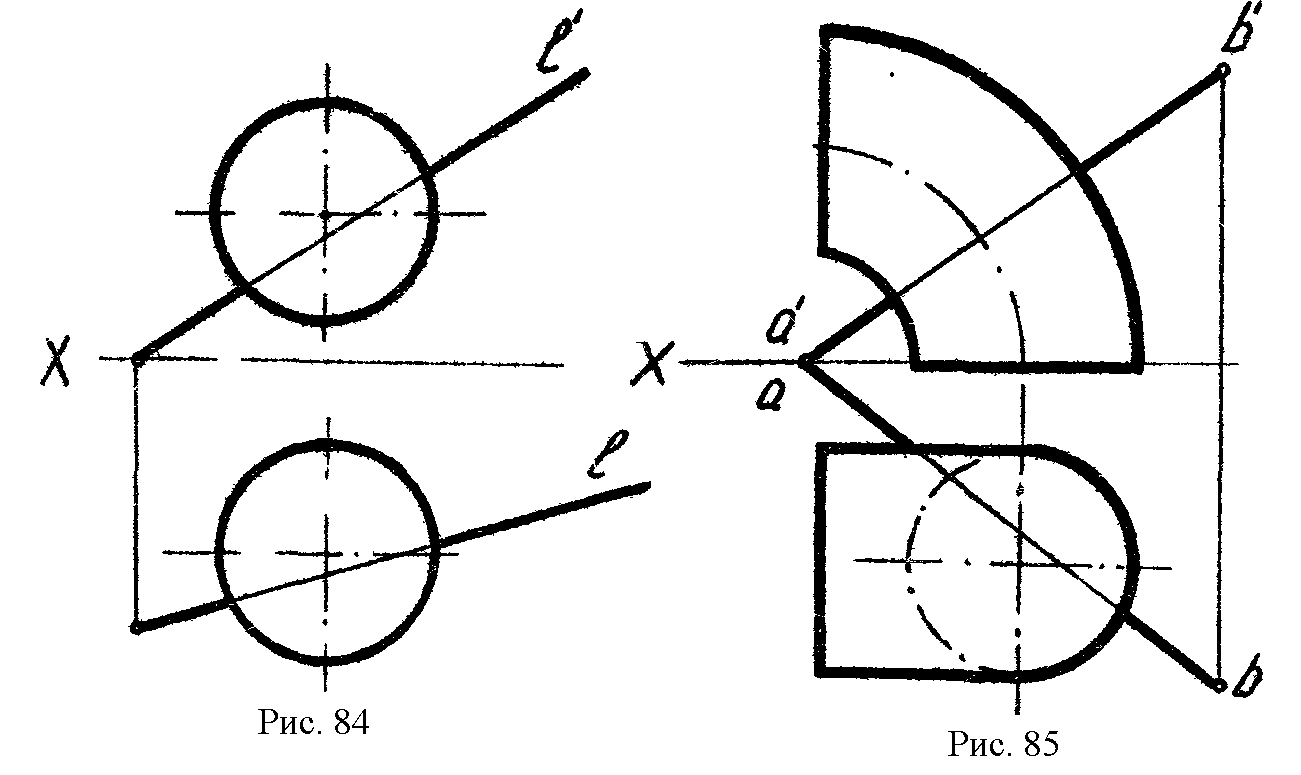
3*.Определить точки пересечения прямой с поверхностью шара (рис. 84).

4*.Определить точки пересечения прямой с поверхностью тора (рис.85).

Тема 14

ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ

Пересечение Способ плоскостей Способ сферических

Многогранников посредников посредников

В пересечении двух многогранников получаются одна или две замкнутые пространственные ломаные линии, состоящие из отрезков прямых, пересекающихся между собой на ребрах многогранника.

В пересечении двух кривых поверхностей получаются в общем случае одна или две пространственные замкнутые плавные кривые (в частных случаях они распадаются на плоские кривые или даже прямые линии).

С троят линию пересечения по отдельным точкам. Общим способом построения этих точек является способ поверхностей посредников. Пересекая данные поверхности некоторой вспомогательной поверхностью и определяя линии пересечения ее с обеими данными поверхностями, в пересечении этих линий получают точки, принадлежащие искомой линии пересечения.

Выбирают посредники так, чтобы линии их пересечения с данными поверхностями были наиболее, простыми, например, прямыми или окружностями.

В зависимости от характера пересекающихся поверхностей в качестве посредников могут быть приняты плоскости частного положения, сферические поверхности и др.

Литература: [1, c.117-122, 250-253]; [2, c. 118-121,194-225]

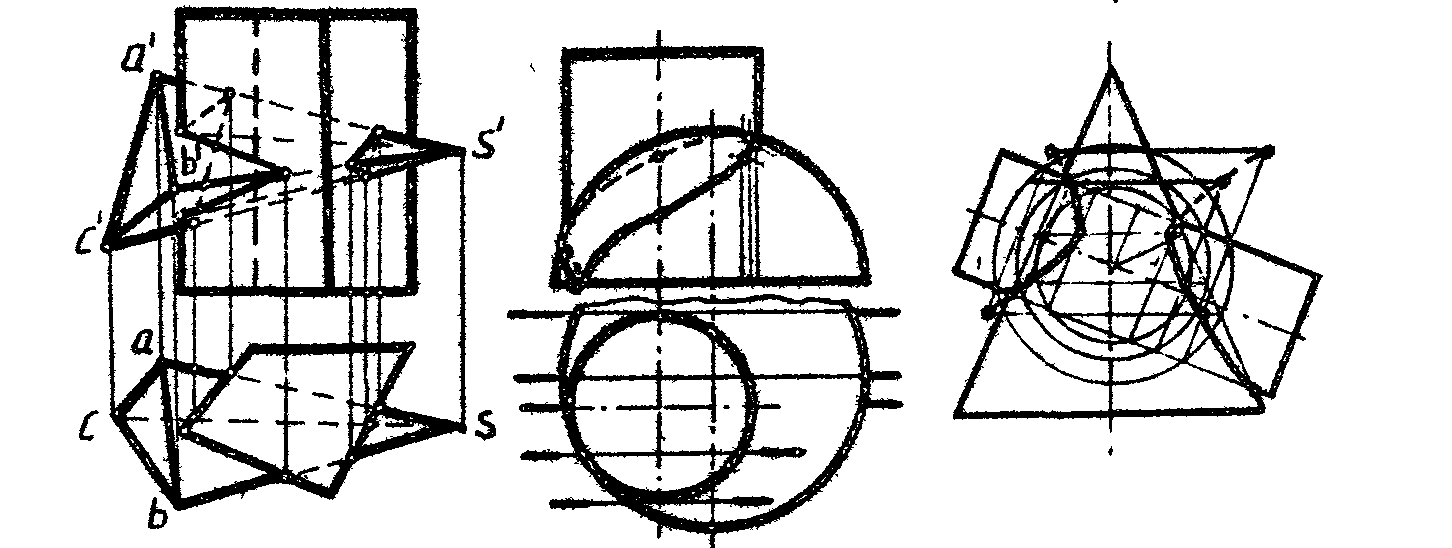
1. По наглядному изображению построить комплексный чертеж точек А, В, С (рис. 1).

2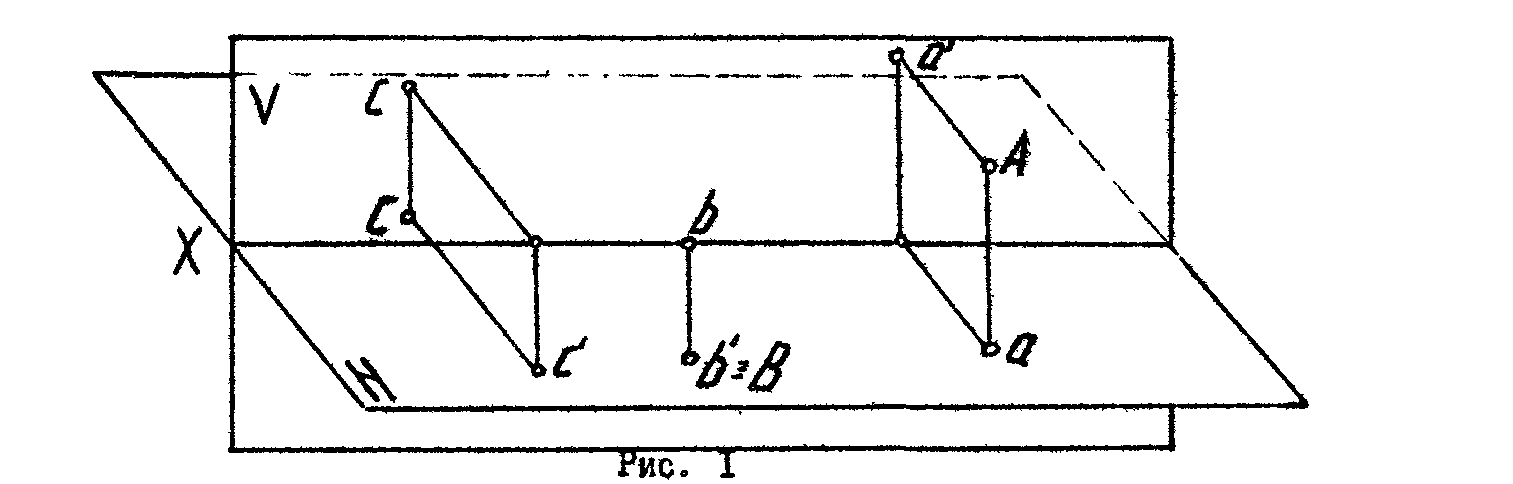 *. Построить изображения точек А (25, 20, 75) и В (20, 25,0) на комплексном чертеже и на наглядном изображении по образцу точки С (35, 10, 30.) (рис.2).

3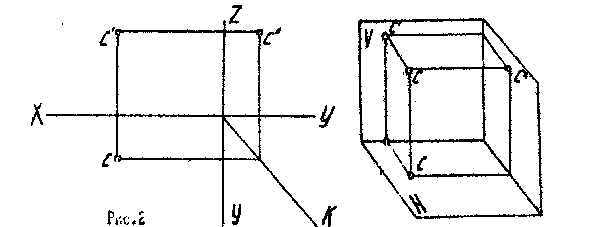 *. По двум проекциям точек А, В, С, D построить третьи проекции и их наглядное изображение (рис. 3).

Т Е М А 1.

ТОЧКА И ЕЕ ПРОЕКЦИИ

Точка в системе двух Точка в системе трех

плоскостей проекций плоскостей проекций

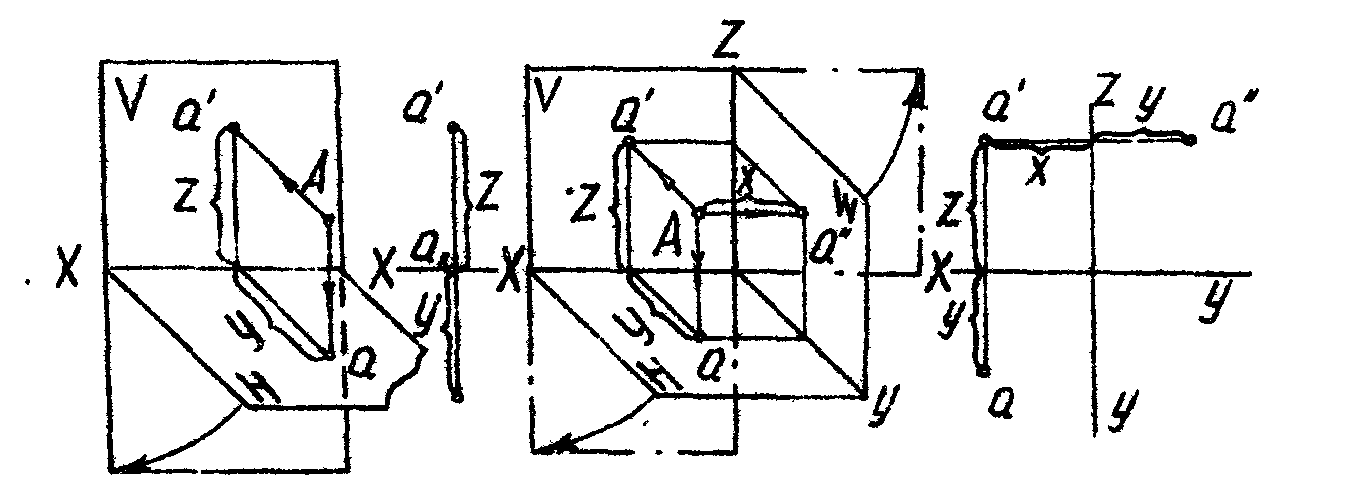
Положение точки в пространстве определяется ее координатами X, У, Z .т.е. расстоянием от точки до трех плоскостей проекций.

Проекцией точки называется точка пересечения проецирующего луча с плоскостью проекций.

Э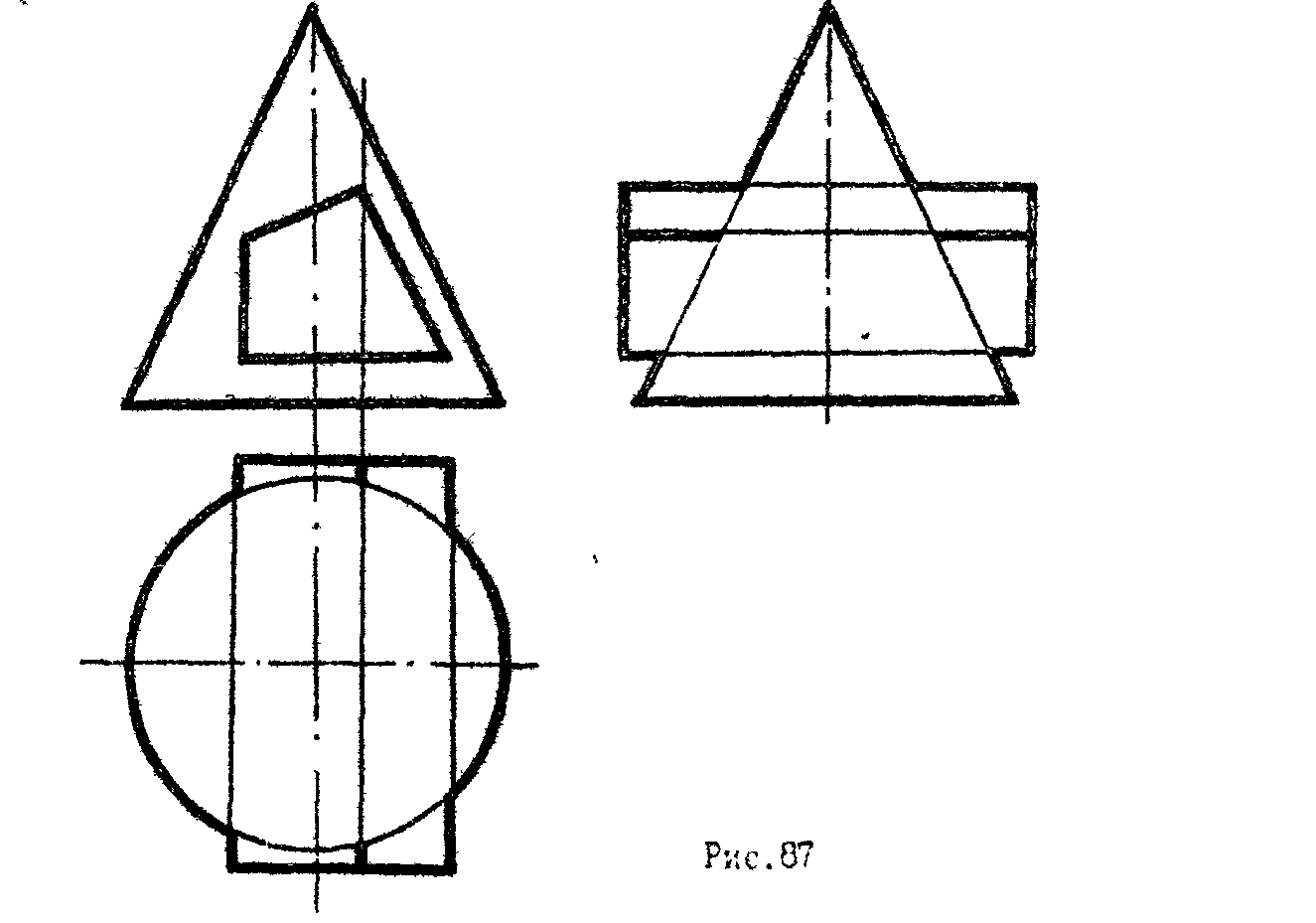 пюром (комплексный чертежом) называется плоский чертеж, полученный совмещением горизонтальной (Н) и профильной (W) плоскостей проекций с фронтальной (V) плоскостью проекций вращением H и W соответственно вокруг осей Х и Z. На эпюре фронтальная и горизонтальная проекции точки всегда располагаются на одной вертикальной линии связи (а’aX). Фронтальная и профильная проекции всегда находятся на одной горизонтальной линии связи (а’a’’Z)

Расстояние от фронтальной проекции точки до оси X является высотой точки (расстоянием от точки до плоскости Н ), численное значение высоты определяется координатой Z. Аналогично, расстояние от горизонтальной проекции точки до оси X является глубиной точки (расстоянием от точки до плоскости V). Численное значение глубины определяется координатой У.

Литература: [1, с.20-29]; [2, с. 15-20, с.24-25].

1. Построить проекции линии пересечения двух тел (рис.86.а,б).

2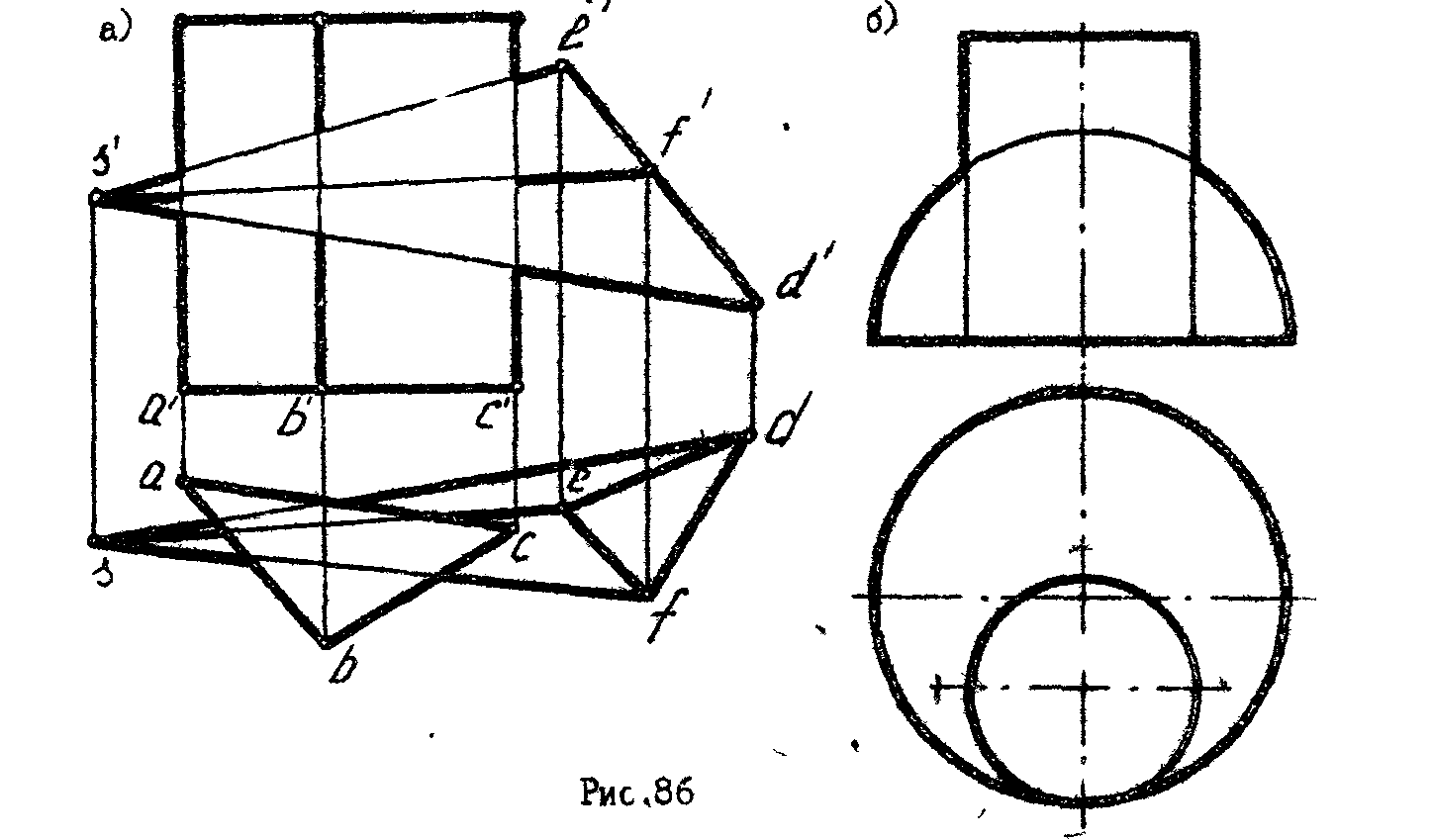 * Построить три проекции линии взаимного пересечения двух поверхностей (рис .87).

3. Построить проекции линии пересечения двух тел (рис.88,а,б).

4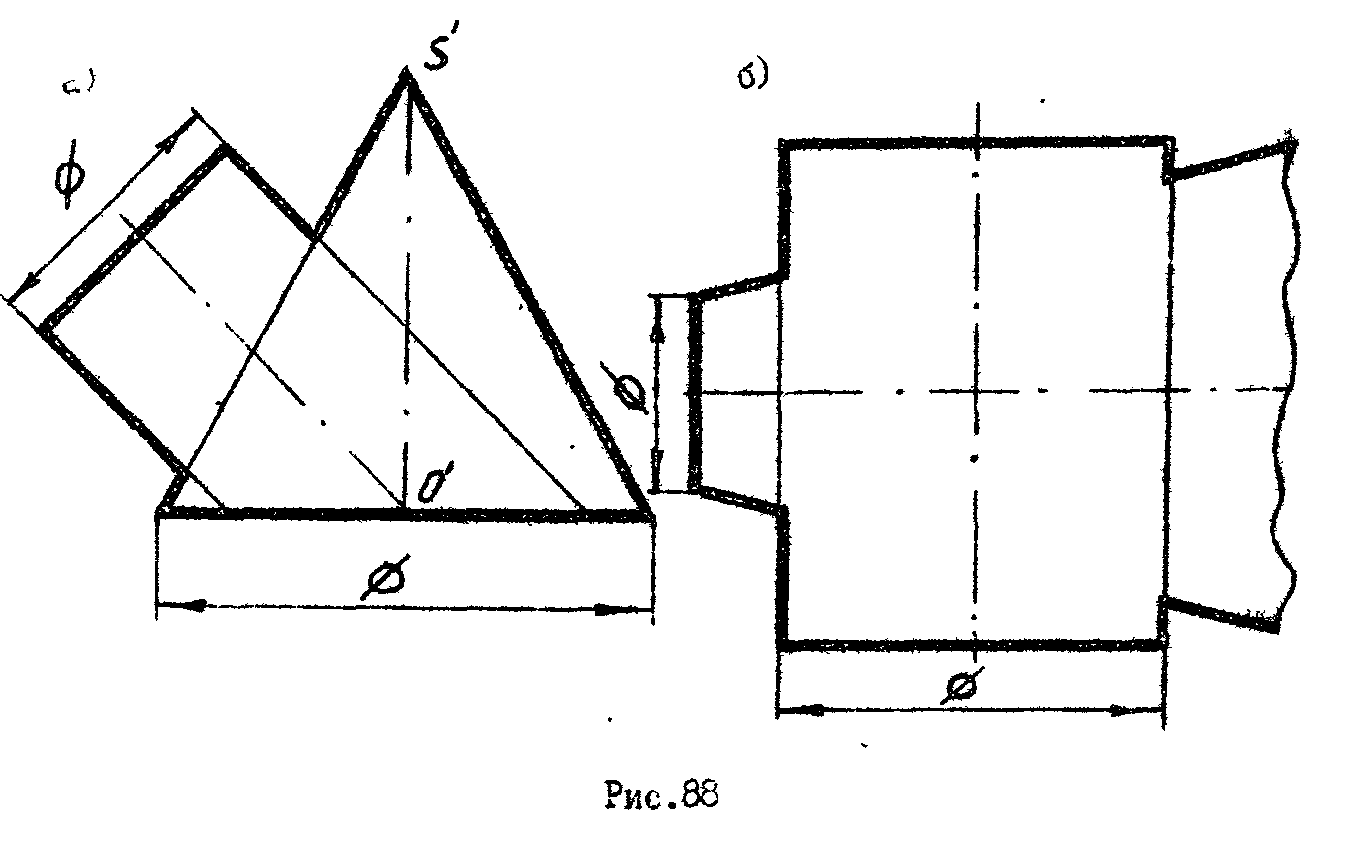 *t. Построить проекции линии пересечения конусе и гора (рис.89)-

Методические указания и упражнения предназначены для студентов всех специальностей при изучении предметов "Начертательная геометрия" и "Инженерная графика".

При работе с методическими указаниями студент должен изучить материал по рекомендуемой литературе, которая указывается в каждой теме.

Цель проведения упражнений: закрепить знания теоретического материала, связать их с практическими примерами, освоить графические приемы решения задач, способствовать развитию пространственного представления.

Упражнения по курсу разбиты на 14 тем. К каждой теме дается краткое изложение теории, указывается литература, в также приводятся условия задач. Задачи, помеченные звездочкой, решаются дома, остальные - в аудитории.

Студент должен ознакомиться с темой занятия, прочитать указанную литературу.

Решение задач выполняется и тетради карандашом с применением чертежных инструментов и цветных карандашей (фломастеров или шариковых ручек с цветными пастами). Домашние задачи решаются в отдельной тетради.

В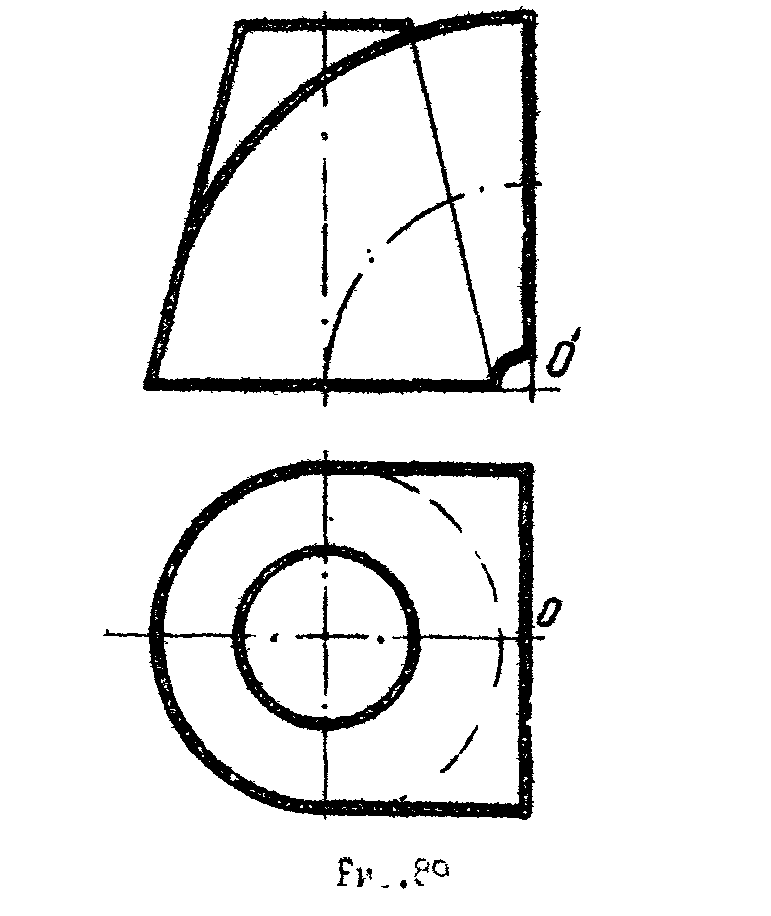 связи с тем, что студенту приходится решать задачи, относящиеся к пространственным предметам, необходимо все построения мысленно представлять в пространстве. Полезно прибегать к изготовлению простейших моделей (из бумаги, картона и т.п.), а также к выполнению пространственных чертежей.

В процессе изучения материала в соответствии с календарным планом студент выполняет графические домашние работы (эпюры). Условия эпюрных задач и образцы их оформления приведены на стенде.

Консультации проводятся преподавателем еженедельно по кафедральному расписанию. На них проверяются и принимаются домашние работы студентов, проводится повторный программированный контроль знаний, даются пояснения по различным вопросам курса.

В конце семестра студент должен сдать экзамен. К экзамену допускаются студенты, выполнившие и защитившие все расчетно -графические работы.

В работе дано краткое описание теории по отдельным темам курса, приведены условия задач, указана литература.

Методические указания предназначены для студентов всех специальностей при изучении предметов «Начертательная геометрия» и «Инженерная графика».

Составители: Чернышова Э.И. – старший преподаватель

Валитова Э.Г. - старший преподаватель

Рецензент: Глущенко И.Ф.; доцент, к.т.н.

© Уфимский государственный нефтяной технический университет, 2001

Литература:

1. Бубенников А.В., Громов М.Я. Начертательная геометрия – М.: Высшая школа, 1973. – 416с.

2. Гордон В.О., Семенцов – Ошевский М.А. Курс начертательной геометрии – М.: Наука, 1988. – 272с.

Содержание:

Тема 1. Точка и ее проекции 2

Тема 2. Прямая, ее проекции и следы 6

Тема 3. Взаимные положения прямых 9

Тема 4. Плоскость. Прямая и точка в плоскости 12

Тема 5. Взаимное положение двух плоскостей.

Взаимное положение прямой и плоскости 15

Тема 6. Перпендикулярность прямой и плоскости,

двух плоскостей 19

Тема 7. Геометрические места 22

Тема 8. Способ замены плоскостей проекций 25

Тема 9. Способ вращения вокруг проецирующей оси.

Плоско – параллельные перемещения 28

Тема 10. Вращение вокруг линии уровня, совмещение. 31

Тема 11. Кривые линии и поверхности 34

Тема 12. Сечение поверхностей тела плоскостью.

Развертки. 37

Тема 13. Пересечение прямой линии с поверхностью. 40

Тема 14. Взаимное пересечение поверхностей 42

ЛИТЕРАТУРА 45

Министерство образования Российской федерации

Уфимский государственный нефтяной технический университет

Стерлитамакский филиал