
- •Глава 3. Аналитическая геометрия на плоскости.
- •Тема 1. Уравнение линии на плоскости.
- •Тема 2. Геометрические задачи на прямую на плоскости.
- •Тема 3. Кривые 2-го порядка
- •Глава 4. Аналитическая геометрия в пространстве.
- •Тема 1. Уравнения линий и поверхностей в пространстве.
- •Тема 2. Прямая и плоскость в пространстве.
- •Тема 3. Поверхности 2-го порядка.
- •Глава 3. Аналитическая геометрия на плоскости
- •Тема 1. Уравнение линии на плоскости.
- •Тема 2. Геометрические задачи на прямую на плоскости.
- •Тема 3. Кривые 2-го порядка
- •Глава 4. Аналитическая геометрия в пространстве.
- •Тема 1. Уравнения линий и поверхностей в пространстве.
- •Тема 2. Прямая и плоскость в пространстве.
- •Тема 3. Поверхности 2-го порядка.
Глава 4. Аналитическая геометрия в пространстве.
Тема 1. Уравнения линий и поверхностей в пространстве.
. Установить, какие поверхности задаются следующими уравнениями в прямоугольной декартовой системе координат в пространстве. Изобразить схематически эти поверхности.
1.
xyz
= 0 2. xz
= 0 3. z - 3 = 0
4. x2
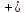 y2
y2
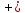 z2 = 4
z2 = 4
5. 2x2
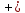 3y2
3y2
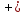 5z2 = 0 6.
y2
5z2 = 0 6.
y2
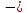 xy
= 0 7. (x
xy
= 0 7. (x
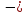 1)2
1)2
 (y - 3)2
(y - 3)2
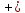 (z + 2)2 = 9
(z + 2)2 = 9
8.
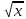
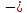
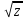 = 0 9.
= 0 9.
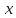 2 +
2 +
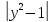 + z2 + 1 = 0
10.
+ z2 + 1 = 0
10.

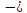
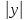 = 0
= 0
. Составить уравнение плоскости в пространстве и привести его к общему виду.
1.
Нормальное уравнение:
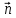
, M
, M
а)
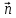 {1; 2; -3}, M(3; -2; 4); б)
{1; 2; -3}, M(3; -2; 4); б)
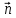 {-1; 2; 0}, M(2; -1; 3); в)
{-1; 2; 0}, M(2; -1; 3); в)
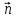 {3; 0; 2}, M(-3; 5; 1)
{3; 0; 2}, M(-3; 5; 1)
2. Уравнение плоскости, проходящей через 3 точки: M1 , M2 , M3
а) M1(3; -2; 4), M2(-3; 5; 1), M3(1; 0; 2); б) M1(1; -2; 0), M2(-2; 3; 2), M3(0; 3; 1)
3. Уравнение плоскости « в отрезках»: A(a; 0; 0) , B(0; b; 0) , C(0; 0; c)
а) a = 4, b = 3; c = -2; б) a = - 3, b = 2; c = -1; в) a = 2, b = -1; c = 3
4.
Нормированное уравнение:
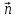 {cos α; cos
{cos α; cos
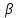 ;
cos
;
cos
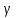 }
, d(
}
, d(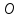 ;
)
= p
;
)
= p
а)
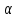 =
=
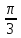 ,
,
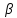 =
=
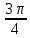 ,
,
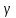 =
=
 ,
p = 4; б)
,
p = 4; б)
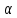 =
=
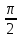 ,
,
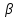 =
=
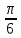 ,
,
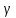 =
=
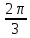 ,
p = 3; г)
,
p = 3; г)
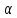 =
=
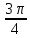 ,
,
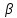 =
=
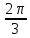 ,
,
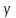 =
=
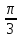 ,
p = 5
,
p = 5
5. «Неполное» уравнение:
а)
‖ OXY,
 OZ
= (0; 0; 3); б)
‖ OXZ,
OZ
= (0; 0; 3); б)
‖ OXZ,
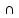 OY
= (0; -4; 0); в)
‖ OYZ,
OY
= (0; -4; 0); в)
‖ OYZ,
 OX
= (2; 0; 0); г)
‖ OZ,
OX
= (2; 0; 0); г)
‖ OZ,
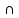 OX
= (1; 0; 0),
OX
= (1; 0; 0),
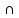 OY
= (0; 2; 0); д)
‖ OY,
OY
= (0; 2; 0); д)
‖ OY,
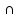 OX
= (-2; 0; 0),
OX
= (-2; 0; 0),
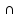 OZ
= (0; 0; 3); е)
‖ OX,
OZ
= (0; 0; 3); е)
‖ OX,
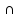 OY
= (0; -2; 0),
OY
= (0; -2; 0),
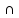 OZ
= (0; 0; 5)
OZ
= (0; 0; 5)
. Установить, какие линии задаются следующими уравнениями в прямоугольной декартовой системе координат в пространстве. Изобразить схематически эти линии.
1.
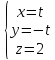 , t(-;
+)
2.
, t(-;
+)
2.
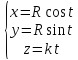 , t(-;
+), R
> 0 3.
, t(-;
+), R
> 0 3.
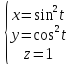 ,
t(-;
+)
,
t(-;
+)
4.
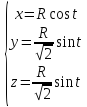 , t[0;
2],
R > 0 5.
, t[0;
2],
R > 0 5.
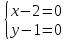 6.
6.
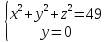
7.
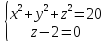 8.
8.
 9.
9.
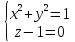
10.
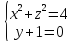 11.
11.
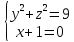 12.
12.
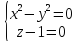
. Составить канонические и параметрические уравнения прямой линии L в пространстве.
1.
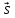 ‖
L,
M
L
‖
L,
M
L
а)
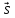 {1; 2; -4}, M(-3; 5; 0); б)
{1; 2; -4}, M(-3; 5; 0); б)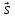 {2; 0; -1}, M(3; -2; 2); в)
{2; 0; -1}, M(3; -2; 2); в)
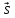 {5; 3; 0}, M(0; -3; 4)
{5; 3; 0}, M(0; -3; 4)
2. M1 L, M2 L
а) M1(1; 2; -7), M2(0; -3; 5); б) M1(-1; 0; 5), M2(2; 2; -1); в) M1(0; 5; 0), M2(3; -1; 2)
3. L
= 1
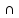 2
2
а) 1: 3x - y + 2z - 7 = 0, 2: x + 3y - 2z - 3 = 0; б) 1: 2x - 3y - 3z - 9 = 0, 2: x - 2y + z + 3 = 0
Тема 2. Прямая и плоскость в пространстве.
1. Составить уравнение плоскости, проходящей через точку M параллельно плоскости .
а) M(1; 1; 1), : 2x - y + z - 1 = 0; б) M(1; 1; 2), : x - y - 1 = 0
2. Составить уравнение плоскости, проходящей через точки M1 и M2 перпендикулярно к плоскости .
а) M1(1; 2; 0), M2(2; 1; 1), : x - y + 1 = 0; б) M1(0; 1; 1), M2(2; 0; 1), : 2x - y + z + 1 = 0
3. Составить уравнение плоскости, проходящей через точку M параллельно векторам a1, a2.
а) M(1; 1; 1), a1{0; 1; 2}, a2{-1; 0; 1}; б) M(0; 1; 2), a1{2; 0; 1}, a2{1; 1; 0}
4. Составить уравнение плоскости, проходящей через точки M1 и M2 параллельно вектору a.
а) M1(1; 2; 0), M2(2; 1; 1), a {3; 0; 1}; б) M1(1; 1; 1), M2(2; 3; -1), a {0; -1; 2}
5. Составить уравнение плоскости, проходящей через точку M (1; 1; -1) и перпендикулярной к плоскостям: 2x - y + 5z + 3 = 0 и x + 3y - z - 7 = 0.
6. Вычислить объем пирамиды, ограниченной плоскостью 2x - 3y + 6z - 12 = 0 и координатными плоскостями.
7. Составить уравнение плоскости, проходящей через точку M (1; 7; -5) и отсекающей от осей координат положительные и равные отрезки.
8. Составить уравнение плоскости, делящей пополам двугранный угол, образованный плоскостями: x - 3y + 2z - 5 = 0 и 3x - 2y - z + 3 = 0.
9. В пирамиде ABCD найти двугранный угол между боковой гранью [DAB] и основанием [ABC], если известно: A(2; 0; 0), B(5; 3; 0), C(0; 1; 1), D(-2; -4; 1).
10. Найти расстояния от точки A (-2; 1; -1) до плоскости, проходящей через точки M1(1; 0; 0), M2(1; 5; -4), M3(3; -1; 2).
11.
Составить канонические уравнения
прямой, проходящей через точку M
(2; -5; 3) и
 прямой:
прямой:
а)
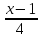 =
=
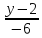 =
=
 ;
б)
;
б)
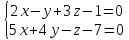
12.
Вычислить угол между прямыми:
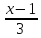 =
=
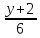 =
=
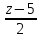 и
и
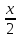 =
=
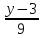 =
=
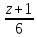
13.
Вычислить угол между прямыми:
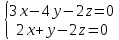 и
и
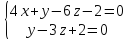
14. Составить канонические уравнения прямой, проходящей через точку M (3; -2; 4) и перпендикулярной к плоскости 5x + 3y - 7z + 1 = 0.
15. Найти
точку пересечения прямой
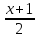 =
=
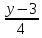 =
=
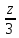 и плоскости 3x - 3y
+ z + 18 = 0.
и плоскости 3x - 3y
+ z + 18 = 0.
16. Найти проекцию точки A (4; -3; 1) на плоскость x + 2y - z - 3 = 0.
17.
Составить уравнение плоскости, проходящей
через точку M (3;
1; -2) и прямую
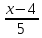 =
=
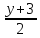 =
=
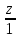
18.
Составить уравнение плоскости, проходящей
через прямую
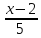 =
=
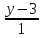 =
=
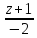 и перпендикулярной к плоскости x
+ 4y - 3z + 7 =
0.
и перпендикулярной к плоскости x
+ 4y - 3z + 7 =
0.
19. Составить уравнение плоскости, проходящей через 2 параллельные прямые
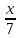 =
=
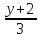 =
=
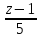 и
и
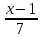 =
=
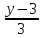 =
=
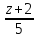
20.
Составить уравнение плоскости, проходящей
через прямую
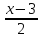 =
=
 =
=
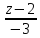 и параллельной прямой
и параллельной прямой
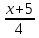 =
=
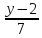 =
=
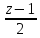 .
.
21.
Составить уравнение плоскости, проходящей
через прямую
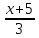 =
=
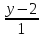 =
=
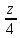 и параллельной плоскости x
+ y - z + 15 = 0.
и параллельной плоскости x
+ y - z + 15 = 0.
22. Найти
расстояние от точки P(7;
9; 7) до прямой
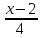 =
=
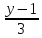 =
=

23. Найти точку M, симметричную точке M (2; -1; 1) относительно плоскости x - y + 2z - 2 = 0.
24. Найти
точку M,
симметричную точке M
(2; -1; 1) относительно прямой
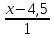 =
=
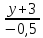 =
=
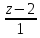 .
.
25. Найти
расстояние между прямыми
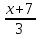 =
=
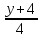 =
=
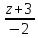 и
и
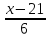 =
=
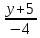 =
=
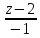 .
.
26. Найти
расстояние между параллельными прямыми
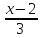 =
=
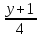 =
=
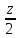 и
и
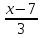 =
=
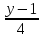 =
=
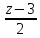 .
.
27. Найти
угол между прямой
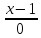 =
=
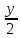 =
=
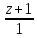 и плоскостью x + y
- z + 1 = 0.
и плоскостью x + y
- z + 1 = 0.
28. В пирамиде ABCD найти угол между боковым ребром [DB] и основанием [ABC], если известно: A(2; 0; 0), B(5; 3; 0), C(0; 1; 1), D(-2; -4; 1).
Дополнительные задачи.
1.
Составить канонические уравнения
проекции прямой
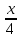 =
=
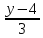 =
=
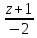 на плоскость x
- y + 3z + 8 = 0.
на плоскость x
- y + 3z + 8 = 0.
2.
Составить канонические уравнения
прямой, проходящей через точку M
(3; -2; -4), параллельной плоскости 3x
- 2y - 3z - 7 = 0
и пересекающей прямую
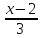 =
=
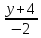 =
=
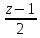 .
.
3. Составить уравнение плоскости, проходящей через 2 пересекающиеся прямые
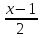 =
=
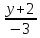 =
=
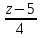 и
и
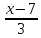 =
=
 =
=
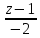
4.
Вычислить угол между прямой:
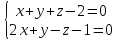 и плоскостью, проходящей через
точки
и плоскостью, проходящей через
точки
M1(2; 3; -1), M2(1; 1; 0), M3(0; -2; 1).
5. Дан треугольник ABC: A(4; 1; -2), B(2; 0; 0), C(-2; 3; -5). Составить канонические уравнения его высоты, опущенной из вершины B на противоположную сторону.
6.
Составить канонические уравнения
общего перпендикуляра двух прямых:
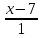 =
=
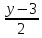 =
=
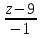 и
и
 =
=
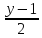 =
=
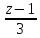 .
.
