Тема 3. Поверхности 2-го порядка.

. Установить, какие поверхности задаются следующими уравнениями 2-го порядка в прямоугольной декартовой системе координат в пространстве. Изобразить схематически эти поверхности.

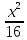
474. x² y² z² = 1 475. = 1 476. = 1 477. y² z² = 4

478. x = 479. = x² 480. = 1 481. y =

482. = 1 483. = z² 484. = 0 485. y = x² z²

. Найти сечения поверхностей 2-го порядка указанными плоскостями; определить параметры полученных линий.

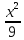
486. = 1 а) x = 2; б) y = 0; в) z = 3

487. = 1 а) x = 0; б) y = 1; в) z = 5

488. x = а) x = -1; б) y = 3; в) z = 0

489. y = x² z² а) x = 3; б) y = 0; в) z = 2

490. = x² а) x = 1; б) y = -5; в) z = -1

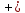
491. = 0 а) x = 0; б) y = 2; в) z = 1

492. = 1 а) x = 5; б) y = 0; в) z = -1

493. y² 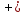z² = 4 а) x = 1; б) y = 2; в) z = 1

.

494. Найти точки пересечения поверхности с прямой L:

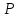а) : = 1, L: = = б) : = 1, L: = =

495. Найти точки пересечения поверхности с прямой L:

а) 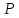: y² = -1, L: x3 = y 1 = б) : = 1, L: = =

496. Составить уравнение цилиндрической поверхности, описанной около сферы

(x a)² y² z² = a² с осью, параллельной: а) оси OX; б) оси OY; в) оси OZ.

497. Составить уравнение цилиндрической поверхности с образующей и направляющей L:

а) {1; 2; 3}, L: б) {1; 1; 1}, L:

498. Найти угол между образующей и осью конуса: x² y² = 0

499. Составить уравнение конуса, если заданы вершина M₀ и направляющая L:

а) M₀(0; -1; 0), L: б) M₀(0; 0; c), L:

500. Составить уравнение поверхности, образованной вращением кривой

вокруг оси: а) OZ; б) OX.

501. Составить уравнение поверхности, образованной вращением прямой

вокруг оси: а) OY; б) OZ.

О Т В Е Т Ы

Глава 1. Л и н е й н а я а л г е б р а

Тема 1. Определители

№	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
	-2	0	2b3	0,5	0		0,5	-0,5	1	60	1	-6	-12	30	20	1	4	5

№	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34
	-2	-14	4	0	2	0	12	9	0	2	-20	10	0	-2000	0	16

№	35	36	37	38	39	40	41	42	43
	120	-168	-1	-126	-24	32	200	-5	-7

Дополнительные задачи

44. P (λ) = (1-λ)(3-λ)(4-λ) = -λ³ + 8λ² - 19λ + 12; λ₁ = 1, λ₂ = 3, λ₃ = 4 45. 0

46. n! 47. 2n + 1 48. n + 1 49. … 

50. 51. 

52.  53. a ⁿ 54. 1 55. n