Тема 3. Кривые 2-го порядка

. Окружность.

364. Построить окружность, найти ее центр C и радиус R:

а) x² + y² - 8x + 6y + 21 = 0; б) x² + y² - 4x = 0; в) x² + y² + 6y - 7 = 0; г) 9x² + 9y² - 6x + 6y - 7 = 0

365. Составить уравнение окружности, проходящей через 3 точки: A(0; 2), B(1; 1), C(2; -2).

366. Составить уравнение окружности, касающейся оси OX в начале координат и пересекающей ось OY в точке A(0; 4).

367. Составить уравнение окружности радиуса R = 2, касающейся оси OY в точке A(0; -3).

368. Составить уравнение окружности, касающейся обеих осей координат и проходящей через точку A(2; 9).

369. Составить уравнение окружности с центром в точке C(6; 7), касающейся прямой 5x - 12y - 24 = 0.

370. Составить уравнение касательной к окружности x² + y² = 5 в точке A(1; -2).

371. Составить уравнение касательной к окружности (x - 1)² + (y - 2)² = 25 в точке A(5; 5).

372. Составить уравнение касательной к окружности x² + y² - 2x - 3y = 0 в точке A(0; 3).

373. Определить угол, под которым видна окружность x² + y² = 16 из точки M(8; 0).

374. Найти длину d касательной, проведенной из точки M(2; 6) к окружности (x + 3)² + (y - 2)² = 25.

375. Составить уравнение окружности, проходящей через точку A(1; 1) и касающейся прямых 7x + y - 3 = 0 и x + 7y - 3 = 0.

. Эллипс.

376. Построить эллипс: 9x² + 25y² = 225. Найти его полуоси a и b, фокусы F₁ и F₂, эксцентриситет e, расстояние между директрисами d; составить уравнения директрис D₁ и D₂.

377. Написать каноническое уравнение эллипса, если известно:

а) a = 3, b = 2; б) a = 5, c = 2; в) c = 3, e = ; г) b = 5, e = ; д) c = 2, d = 5; е) e = 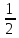, d = 32.

378. Построить эллипс; найти его центр C, полуоси a и b, фокусы F₁ и F₂, эксцентриситет e, расстояние между директрисами d; составить уравнения директрис D₁ и D₂:

а) 5x² + 9y² - 30x + 18y + 9 = 0; б) 16x² +25y² + 32x - 100y - 284 = 0; в) 4x² + 3y² - 8x + 12y - 32 = 0.

379. Вычислить эксцентриситет e эллипса, если известно:

а) малая ось его видна из фокуса под прямым углом;

б) расстояние между фокусами равно расстоянию между вершинами малой и большой осей;

в) расстояние между директрисами в 4 раза больше расстояния между фокусами.

380. На эллипсе 9x² + 25y² = 900 найти точку, расстояние которой от правого фокуса в 4 раза больше расстояния от ее левого фокуса.

381. Через фокус F(c; 0) эллипса + 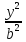= 1 проведена хорда, перпендикулярная к большой оси. Найти длину этой хорды.

382. Составить уравнение касательной к эллипсу + = 1 в точке M(2; -3).

383. Составить уравнения касательных, проведенных из точки A(-6; 3) к эллипсу + = 1.

384. Составить уравнения касательных к эллипсу + = 1, параллельных прямой 2x - y + 17 = 0.

385. Составить уравнения касательных к эллипс у + = 1, перпендикулярных к прямой 13x + 12y - 115 = 0.

. Гипербола.

386. Построить гиперболу: 16x² - 9y² = 144. Найти ее полуоси a и b, фокусы F₁ и F₂, эксцентриситет e, расстояние между директрисами d, угловой коэффициент k асимптот; составить уравнения асимптот L₁ и L₂ и директрис D₁ и D₂.

387. Написать каноническое уравнение гиперболы, если известно:

а) a = 2, b = 3; б) b = 4, c = 5; в) c = 3, e = ; г) a = 8, e = 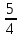; д) c = 10, k =  ; е) e = , d = .

388. Построить гиперболу; найти ее центр C, полуоси a и b, фокусы F₁ и F₂, эксцентриситет e, расстояние между директрисами d; составить уравнения асимптот L₁ и L₂ и директрис D₁ и D₂:

а) 16x² - 9y² - 64x - 54y - 161 = 0; б) 9x² - 16y² + 90x + 32y - 367 = 0; в) 16x² - 9y² - 64x - 18y + 199 = 0.

389. Вычислить эксцентриситет e гиперболы, если известно:

а) угол между асимптотами равен 60; б) угол между асимптотами равен 90;

в) действительная ось гиперболы видна из фокуса сопряженной гиперболы под углом в 60.

390. Найти угол между асимптотами гиперболы, если расстояние между фокусами вдвое больше расстояния между директрисами.

391. На гиперболе = 1 найти точку, расстояние которой от левого фокуса в 2 раза больше расстояния от ее правого фокуса.

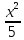
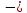
392. Составить уравнение касательной к гиперболе = 1 в точке M(5; -4).

393. Составить уравнения касательных, проведенных из точки A(2; 0) к гиперболе 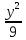= 1.

394. Составить уравнения касательных к гиперболе = 1, параллельных прямой x + y - 7 = 0.

395. Составить уравнения касательных к гиперболе = 1, перпендикулярных к прямой x - 2y = 0.

. Парабола.

396. Построить параболу. Найти ее параметр p, ось симметрии l и фокус F; составить уравнение директрисы D.

а) y² = 6x; б) x² = -y в) y² = - 4x; г) x² = 5y

397. Написать каноническое уравнение параболы, если известно:

а) l = OX, x < 0, p = ; б) l = OY, точка M (4; -8) лежит на параболе; в) F (0; -3) - фокус параболы

398. Построить параболу; найти ее вершину C, параметр p, ось симметрии l и фокус F; составить уравнение директрисы D:

а) y² = 4x - 8; б) x² = 2 - y; в) y = 4x² - 8x + 7; г) x = - y² + y

399. Точка M лежит на параболе y² = 4,5x и находится на расстоянии 9,125 от ее директрисы. Найти расстояние от точки M до вершины параболы.

400. Через фокус параболы y² = 2px проведена хорда, перпендикулярная к ее оси. Найти длину этой хорды.

401. Составить уравнения касательных, проведенных из точки A(5; -7) к параболе y² = 8x .

402. Составить уравнения касательных к параболе y² = 12x, параллельных прямой 3x - y + 5 = 0.

403. Составить уравнения касательных к параболе y² = 12x, перпендикулярных к прямой 2x + y = 7.

Дополнительные задачи.

404. Найти расстояние от эллипса + = 1 до прямой 2x - 3y + 25 = 0.

405. Найти расстояние от гиперболы = 1 до прямой 3x + 2y + 1 = 0.

406. Найти расстояние от параболы y² = 64x до прямой 4x + 3y + 16 = 0.

407. Из левого фокуса эллипса + = 1 под углом α = - arctg 2 ( < α < ) к оси OX направлен луч света. Составить уравнение прямой, на которой лежит луч, отраженный от эллипса.

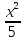
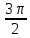408. Из правого фокуса гиперболы = 1 под углом α = arctg 2 ( < α < ) к оси OX направлен луч света. Составить уравнение прямой, на которой лежит луч, отраженный от гиперболы.

409. Из фокуса параболы y² = 12x под углом α = arctg (0 < α < ) к оси OX направлен луч света. Составить уравнение прямой, на которой лежит луч, отраженный от параболы.