Глава 3. Аналитическая геометрия на плоскости.

Тема 1. Уравнение линии на плоскости.

. Построить линии, заданные уравнениями в прямоугольной декартовой системе координат.

298. xy = 0 299. x² y² = 0 300. 5(x + 2)² 7(y 3)² = 0 301. (x + 2)(y - 3) = 0

302. x² 4x + 3 = 0 303. y² y 2 = 0 304. (x y)² (x y)² = 2 305. (x 2y)(2x 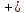y) = 0

306. (x y)² (x y)² = 4 307. + = 1 308. = 1 309. ² + = 0

310. = 0 311. + = 0 312. = 0 313.  = 0

. Построить линии, заданные параметрическими уравнениями в прямоугольной декартовой системе координат.

314. 315. 316. 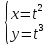317.

318. 319. 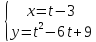320. 321.

322. 323.

.

Составить уравнение прямой L и привести его к общему виду. Построить данную прямую.

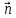
324. Нормальное уравнение:  L , M L

а) {1; 2}, M(-2; 4); б) {-1; 3}, M(2; 1); в) {2; -1}, M(-3; 2); г) 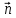{1; 0}, M(-3; -2).

325. Каноническое уравнение: ‖ L , M L

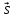а) {1; 2}, M(-3; 5); б) {-1; 3}, M(2; 1); в) {1; -2}, M(3; -1); г) {1; 0}, M(-3; -2).

326. Параметрические уравнения: ‖ L , M L

а) {1; -2}, M(3; 5); б) {-1; 3}, M(-2; 1); в) {2; 3}, M(1; -1); г) {0; 1}, M(-3; 2).

327. Уравнение прямой, проходящей через 2 точки: M₁ L, M₂ L

а) M₁(1; 2), M₂(-3; 5); б) M₁(-1; 3), M₂(2; -4); в) M₁(1; -2), M₂(1; 2); г) M₁(-1; -2), M₂(3; 1).

328. Уравнение прямой « в отрезках»: A(a; 0) L, B(0; b) L

а) a = 4, b = 3; б) a = -3, b = 2; в) a = 1, b = -4; г) a = -2, b = -3.

329. Нормированное уравнение: {cos α; sin α}  L , d(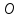; L) = p

а) = , p = 4; б) = , p = 3; в) = , p = 2; г) = - , p = .

330. Уравнение прямой с угловым коэффициентом: (L, OX) = , M L

а) = , M(-3; 5); б) = , M(1; -2); в) = , M(2; 1); г) = , M(0; 3).

331. «Неполное» уравнение: L ‖ OX, L OY = (0; y₀) или L ‖ OY, L OX = (x₀; 0)

а) y₀ = 1; б) x₀ = 4; в) x₀ = -3; г) y₀ = -2.

. Дан треугольник ABC. Составить уравнения сторон треугольника и уравнения: медианы [m_A], высоты [h_A] и биссектрисы [l_A], проведенных из вершины A. Привести уравнения к общему виду. Сделать рисунок.

332. A(-2; 1), B(-6; 4), C(6; 7) 333. A(3; 2), B(6; 6), C(8; -10) 334. A(-3; 1), B(5; 7), C(2; -11)

335. A(-6; -6), B(0; 2), C(-2; -3) 336. A(0; 0), B(2; 2), C(7; 1) 337. A(-2; -1), B(2; -3), C(9; 1)

Тема 2. Геометрические задачи на прямую на плоскости.

338. Найти угол между прямыми L ₁ и L₂.

а) L ₁: = , L ₂: 2x - y + 3 = 0; б) L ₁: , L ₂: + = 1

339. Найти расстояние между параллельными прямыми L ₁ и L₂.

а) L ₁: = 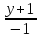, L ₂: x + y - 1 = 0; б) L ₁: , L ₂: =

340. Дан 4-хугольник ABCD: A(-9; 0), B(-3; 6), C(3; 4), D(6; -3). Найти точку пересечения M диагоналей AC и BD и вычислить острый угол  между ними.

341. Найти расстояние от точки M(2; 1) до прямой L:

342. Найти угловой коэффициент «k» прямой, проходящей через точку M(-2; 1) на расстоянии 4-х единиц от точки C(3; 1).

343. Составить уравнение прямой, параллельной двум заданным прямым L ₁ и L₂ и проходящей посередине между ними, L ₁: = , L ₂: 3x - 2y - 1 = 0.

344. Составить уравнение прямой, проходящей через точку M(-2; 3) на одинаковых расстояниях от точек P(5; -1) и Q(3; 7).

345. Составить уравнение прямой, проходящей через точку M(2; 1) под углом 45 к прямой L:

346. Из точки M(5; 4) выходит луч света под углом  = arctg 2 к оси OX и отражается от нее. Составить уравнения падающего и отраженного лучей.

347. Найти расстояния от начала координат до прямых, на которых лежат стороны треугольника ABC: A(-1; 2), B(3; -1), C(0; 4).

348. Найти расстояние от вершины B до медианы, проведенной из точки A в треугольнике ABC: A(1; 2), B(3; 7), C(5; -13).

349. Дан треугольник ABC: A(1,8; 0,4), B(0; 4), C(-3; -2). Найти центр О и радиус r вписанной окружности.

350. Дан треугольник ABC: A(2; 3), B(0; -3), C(4; -1). Найти центр О и радиус R описанной окружности.

351. Найти точку M, симметричную точке M(-2; -9) относительно прямой 2x + 5y - 38 = 0.

352. Найти площадь S треугольника, заключенного между осями координат и прямой x + 2y - 6 = 0.

353. Через точку M(5; 2) провести прямую, отсекающую равные отрезки на осях координат.

354. Через точку M(3; 2) провести прямую так, чтобы ее отрезок, заключенный между осями координат, делился в данной точке пополам.

355. Через точку M(4; -3) провести прямую так, чтобы площадь треугольника, образованного ею и осями координат, была равна 3.

356. Дан треугольник ABC: A(-6; -3), B(-4; 3), C(9; 2). На биссектрисе угла A найти такую точку M, чтобы 4-хугольник ABMC оказался трапецией.

357. Дан треугольник ABC: A(5; 8), B(-2; 9), C(-4; 5). Найти: 1) ортоцентр M₁ (точку пересечения высот); 2) центр описанной окружности M₂ (точку пересечения серединных перпендикуляров); 3) центр тяжести M₃ (точку пересечения медиан). Проверить, лежат ли эти точки на одной прямой.

Дополнительные задачи.

358. Составить уравнения сторон треугольника, зная одну из его вершин A(3; -4) и уравнения двух высот: 7x - 2y - 1 = 0, 2x - 7y - 6 = 0.

359. Составить уравнения сторон треугольника, зная одну из его вершин A(-4; 2) и уравнения двух медиан: 3x - 2y + 2 = 0, 3x + 5y - 12 = 0.

360. Составить уравнения сторон треугольника, зная одну из его вершин A(2; -4) и уравнения двух биссектрис: x + y - 2 = 0, x - 3y - 6 = 0.

361. Составить уравнения сторон треугольника, зная одну из его вершин A(2; 6) и уравнения высоты: x - 7y + 15 = 0 и биссектрисы: 7x + y + 5 = 0, проведенных из одной вершины.

362. Составить уравнения сторон треугольника, зная одну из его вершин A(2; -7) и уравнения высоты: 3x + y + 11 = 0 и медианы: x + 2y + 7 = 0, проведенных из различных вершин.

363. Составить уравнения сторон треугольника, зная одну из его вершин A(3; -1) и уравнения биссектрисы: x - 4y + 10 = 0 и медианы: 6x + 10y - 59 = 0, проведенных из различных вершин.