
- •Глава 1. Линейная алгебра.
- •Тема 1. Определители.
- •Тема 2. Матрицы.
- •Тема 3. Системы линейных уравнений.
- •Глава 2. Векторная алгебра.
- •Тема 1. Линейные действия с векторами.
- •Тема 2. Умножение векторов.
- •Тема 3. Прямоугольная декартова система координат.
- •Глава 3. Аналитическая геометрия на плоскости.
- •Тема 1. Уравнение линии на плоскости.
- •Тема 2. Геометрические задачи на прямую на плоскости.
- •Тема 3. Кривые 2-го порядка
- •Глава 4. Аналитическая геометрия в пространстве.
- •Тема 1. Уравнения линий и поверхностей в пространстве.
- •Тема 2. Прямая и плоскость в пространстве.
- •Тема 3. Поверхности 2-го порядка.
- •Глава 1. Л и н е й н а я а л г е б р а
- •Тема 1. Определители
- •Тема 2. Матрицы
- •Тема 3. Системы линейных уравнений
- •Глава 2. В е к т о р н а я а л г е б р а
- •Тема 1. Линейные действия с векторами
- •Тема 2. Умножение векторов
- •Тема 3. Прямоугольная декартова система координат
- •Глава 3. Аналитическая геометрия на плоскости.
- •Тема 1. Уравнение линии на плоскости.
- •Тема 2. Геометрические задачи на прямую на плоскости.
- •Тема 3. Кривые 2-го порядка
- •Глава 4. Аналитическая геометрия в пространстве.
- •Тема 1. Уравнения линий и поверхностей в пространстве.
- •Тема 2. Прямая и плоскость в пространстве.
- •Тема 3. Поверхности 2-го порядка.
Тема 2. Умножение векторов.
.
Даны векторы
 .
Известны модули этих векторов и
углы между ними:
.
Известны модули этих векторов и
углы между ними:
p
=
 ,
q =
,
q =
 ,
r =
,
r =
 ,
α =
,
α =

 ,
β =
,
β =

 ,
γ =
,
γ =

 .
Вектор
.
Вектор
 является линейной
является линейной
комбинацией
векторов
 .
Найти модуль вектора
.
Найти модуль вектора
 .
.
178.
 = 2
= 2 - 3
- 3 ,
p = 1, q = 2, α =
,
p = 1, q = 2, α =
 179.
179.
 =
=
 + 2
+ 2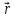 ,
p = 3, r = 1, β =
,
p = 3, r = 1, β =

180.
 = 2
= 2 -
-
 ,
q = 4, r = 2, γ =
,
q = 4, r = 2, γ =
 181.
181.
 =
=
 - 2
- 2 ,
p = 2, q = 1, α =
,
p = 2, q = 1, α =

182.
 =
=
 + 2
+ 2 -
-
 ,
p = 1, q = 1, r = 2, α =
,
p = 1, q = 1, r = 2, α =
 , β =
, β =
 , γ =
, γ =

183.
 = 2
= 2 -
-
 +
+
 ,
p = 1, q = 2, r = 1, α =
,
p = 1, q = 2, r = 1, α =
 , β =
, β =
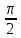 , γ =
, γ =

184.
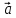 =
=
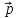 + 2
+ 2 +
+
 ,
p = 3, q = 1, r = 2, α =
,
p = 3, q = 1, r = 2, α =
 , β =
, β =
 , γ =
, γ =

185.
 = 2
= 2 -
-
 -
-
 ,
p = 1, q = 2, r = 3, α =
,
p = 1, q = 2, r = 3, α =
 , β =
, β =
 , γ =
, γ =

 .
Даны единичные векторы
.
Даны единичные векторы
 и угол между ними
α =
и угол между ними
α =

 .
Векторы
.
Векторы
 и
и

являются
линейными комбинациями векторов
 .
На векторах
.
На векторах
 и
и
 построен
построен
параллелограмм. Найти площадь S этого параллелограмма и длины его диагоналей d1 и d2.





d1
d2


186.
 =
=
 + 3
+ 3 ,
,
 = 3
= 3 -
-
 ,
α =
,
α =
 187.
187.
 = 3
= 3 +
+
 ,
,
 =
=
 -
-
 ,
α =
,
α =

188.
 =
=
 - 2
- 2 ,
,
 =
=
 +4
+4 ,
α =
,
α =
 189.
189.
 =
=
 + 3
+ 3 ,
,
 =
=
 - 5
- 5 ,
α =
,
α =

190.
 = 2
= 2 -
-
 ,
,
 =
=
 + 3
+ 3 ,
α =
,
α =
 191.
191.
 = 3
= 3 +
+
 ,
,
 =
=
 - 5
- 5 ,
α =
,
α =

192.
 =
=
 - 4
- 4 ,
,
 = 3
= 3 + 2
+ 2 ,
α =
,
α =
 193.
193.
 =
=
 + 4
+ 4 ,
,
 =
=
 - 2
- 2 ,
α =
,
α =

 .
Найти объем параллелепипеда,
построенного на векторах
.
Найти объем параллелепипеда,
построенного на векторах
 ,
,
 ,
, ,
если известны модули этих векторов и
углы между ними:
,
если известны модули этих векторов и
углы между ними:
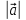 = a,
= a,
 = b,
= b,
 = c, α
=
= c, α
=

 ,
β =
,
β =

 ,
γ =
,
γ =

 .
.
194.
a = 1,
b =
2, c
=
3,
α =
 , β =
, β =
 , γ =
, γ =
 195.
a = 2,
b =
2, c
=
3,
α =
195.
a = 2,
b =
2, c
=
3,
α =
 , β =
, β =
 , γ =
, γ =

196.
a = 1,
b =
2, c
=
4,
α =
 , β =
, β =
 , γ =
, γ =
 197.
a = 2,
b =
1, c
=
2,
α =
197.
a = 2,
b =
1, c
=
2,
α =
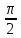 , β =
, β =
 , γ =
, γ =

198.
a = 3,
b =
2, c
=
2,
α =
 , β =
, β =
 , γ =
, γ =
 199.
a = 2,
b =
3, c
=
3,
α =
199.
a = 2,
b =
3, c
=
3,
α =
 , β =
, β =
 , γ =
, γ =

200.
a = 1,
b =
2, c
=
4,
α =
 , β =
, β =
 , γ =
, γ =
 201.
a = 2,
b =
3, c
=
2,
α =
201.
a = 2,
b =
3, c
=
2,
α =
 , β =
, β =
 , γ =
, γ =

Дополнительные задачи.
202. В квадрат ABCD со стороной a вписана окружность. Точка M - произвольная точка этой окружности. Найти сумму MA2 + MB2 + MC2 + MD2.
203. Около квадрата ABCD со стороной a описана окружность. Точка M - произвольная точка этой окружности. Найти сумму MA2 + MB2 + MC2 + MD2.
204. В куб со стороной a вписана сфера. Точка M - произвольная точка этой сферы. Найти сумму квадратов расстояний от точки M до вершин куба.
205.
Найти отношение объема тетраэдра,
построенного на некомпланарных векторах
 ,
,
 ,
, ,
к объему тетраэдра, построенного на
векторах
,
к объему тетраэдра, построенного на
векторах
 +
+ ,
,
 ,
,
 .
.
Тема 3. Прямоугольная декартова система координат.

Рене Декарт (1596 - 1650)
. Построить
вектор

 в прямоугольной декартовой системе
координат и указать его направляющие
углы. Найти модуль и направляющие cos-ы
вектора
в прямоугольной декартовой системе
координат и указать его направляющие
углы. Найти модуль и направляющие cos-ы
вектора
 .
.

206.
 207.
207.

 208.
208.

 209.
209.


210.
 211 .
211 .

 212.
212.

 213 .
213 .


214.

 215.
215.

 216.
216.

 217.
217.

 .
Даны векторы в прямоугольной декартовой
системе координат:
.
Даны векторы в прямоугольной декартовой
системе координат:
 и
и
 .
Вычислить:
.
Вычислить:
1) скалярное произведение


2) проекции

 ,
,


3) векторное произведение

4) площадь параллелограмма, построенного
на этих векторах
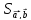
218.
 ,
,
 219.
219.
 ,
,
 220.
220.
 ,
,

221.
 ,
,
 222.
222.
 ,
,
 223.
223.
 ,
,

224.
 ,
,
 225.
225.
 ,
,
 226.
226.
 ,
,

227.
 ,
,
 228.
228.
 ,
,
 229.
229.
 ,
,

. Даны векторы в прямоугольной декартовой системе координат:
 ,
,
 ,
,
 .
Требуется:
.
Требуется:
1) вычислить
смешанное произведение
 2) определить ориентацию этих
векторов
2) определить ориентацию этих
векторов
3) найти
объем
 параллелепипеда, построенного на этих
векторах
параллелепипеда, построенного на этих
векторах
230.
 ,
,
 ,
,
 231.
231.
 ,
,
 ,
,

232.
 ,
,
 ,
,
 233.
233.
 ,
,
 ,
,

234.
 ,
,
 ,
,
 235.
235.
 ,
,
 ,
,

236.
 ,
,
 ,
,
 237.
237.
 ,
,
 ,
,

238.
 ,
,
 ,
,
 239.
239.
 ,
,
 ,
,
240.
 ,
,
 ,
,
 241.
241.
 ,
,
 ,
,

. Даны
векторы
 в прямоугольной декартовой системе
координат. Векторы
в прямоугольной декартовой системе
координат. Векторы
 и
и

являются линейными комбинациями этих векторов. Определить:
- при каких значениях α и β
векторы
 и
и
 будут коллинеарны (№ 242
÷ 245)
будут коллинеарны (№ 242
÷ 245)
- при каких значениях λ векторы
 и
и
 будут ортогональны (№ 246
÷ 249)
будут ортогональны (№ 246
÷ 249)
- при каких значениях λ векторы
 ,
,
 и
и
 будут компланарны (№ 250 ÷
253)
будут компланарны (№ 250 ÷
253)
242.
 = 2
= 2 + 4
+ 4 ,
,
 = 3
= 3 -
-
 ,
,
 ,
,

243.
 =
=
 + 2
+ 2 ,
,
 = 3
= 3 -
-
 ,
,
 ,
,

244.
 = 5
= 5 + 3
+ 3 ,
,
 = 2
= 2 -
-
 ,
,
 ,
,

245.
 = -2
= -2 +
+
 ,
,
 = 3
= 3 - 2
- 2 ,
,
 ,
,

246.
 =
=
 -
-
 ,
,
 = 4
= 4 + 2
+ 2 ,
,
 ,
,

247.
 =3
=3 - 2
- 2 ,
,
 = -2
= -2 +
+
 ,
,
 ,
,

248.
 = 2
= 2 -
-
 ,
,
 = -
= - + 3
+ 3 ,
,
 ,
,

249.
 = 2
= 2 - 3
- 3 ,
,
 = 2
= 2 +
+
 ,
,
 ,
,

250.
 ,
,
 ,
,

251.
 ,
,
 ,
,

252.
 ,
,
 ,
,

253.
 ,
,
 ,
,

Дополнительные задачи.
254.
Прямоугольная декартова система
координат OXY
на плоскости получена из прямоугольной
декартовой системы координат OXY
параллельным переносом на вектор
 .
Произвольная точка M
на плоскости имеет координаты (x,
y) в одной системе
координат и (x,
y)
- в другой системе координат. Найти связь
между этими координатами.
.
Произвольная точка M
на плоскости имеет координаты (x,
y) в одной системе
координат и (x,
y)
- в другой системе координат. Найти связь
между этими координатами.





 ,
M(x, y),
M(x,
y)
,
M(x, y),
M(x,
y)












255. Прямоугольная декартова система координат OXY на плоскости получена из прямоугольной декартовой системы координат OXY путем поворота осей на угол . Произвольная точка M на плоскости имеет координаты (x, y) в одной системе координат и (x, y) - в другой системе координат. Найти связь между этими координатами.

 ,
M(x, y),
M(x,
y)
,
M(x, y),
M(x,
y)















256.
Даны векторы в прямоугольной декартовой
системе координат:
 ,
,
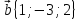 ,
,
 .
Найти координаты вектора
.
Найти координаты вектора
 ,
если известно, что
,
если известно, что
 = -5,
= -5,
 = -11,
= -11,
 = 20.
= 20.
257.
Даны векторы в прямоугольной декартовой
системе координат:
 ,
,
 .
Найти координаты вектора
.
Найти координаты вектора
 ,
если известно, что
,
если известно, что
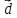
 ,
,

 ,
,
 = 14.
= 14.
.
Точка M
лежит на отрезке AB
и делит его в отношении
 = α : β.
= α : β.
B

M
*
A(x1; y1; z1), B(x2; y2; z2), M(x0; y0; z0)
A
*
*
Координаты двух из этих точек известны. Найти координаты третьей точки.
258. A(1; -2; 6), B(4; 1; 0), α : β = 1 : 2 259. A(0; -2; 6), M(-6; 1; 3), α : β = 3 : 2
260. B(7; 2; -5), M(4; -1; -2), α : β = 2 : 3 261. A(1; -3; 3), B(5; -7; 3), α : β = 1 : 3
262. A(1; -3; 5), M(-1; 3; 1), α : β = 2 : 1 263. B(-2; 2; 1), M(-3; 1; -1), α : β = 5 : 1
264. A(4; -5; 3), B(0; -1; 7), α : β = 3 : 1 265. A(-2; 3; 6), M(1; -3; 3), α : β = 3 : 5
266. B(9; -3; 0), M(4; 2; -5), α : β = 2 : 5 267. A(4; -1; 3), B(-2; -7; 9), α : β = 1 : 5
268. A(0; 3; 2), M(2; 1; -1), α : β = 1 : 4 269. B(3; 2; -1), M(1; 3; -2), α : β = 4 : 1
 .
Найти площадь S,
стороны a, b,
c
и углы
.
Найти площадь S,
стороны a, b,
c
и углы
 A,
A, B,
B, C треугольника
ABC.
C треугольника
ABC.
270. A(5; 3; -1), B(5; 2; 0), C(6; 4; -1) 271. A(1; -2; 3), B(4; 2; -9), C(9; 7; -9)
272. A(3; 3; -1), B(5; 5; -2), C(4; 1; 1) 273. A(6; 2; -3), B(6; 3; -2), C(7; 3; -3)
274. A(2; 1; -1), B(6; -1; -4), C(4; 2; 1) 275 A(-4; -2; 0), B(-1; 2; 12), C(-3; 0; 2)
276. A(0; -3; 6), B(1; -1; 4), C(-1; 9; -6) 277. A(-3; -7; -5), B(6; 5; 15), C(7; 3; 13)
 .
Дана
пирамида A1A2A3A4.
Найти: 1) объем пирамиды V;
2) площадь основания
.
Дана
пирамида A1A2A3A4.
Найти: 1) объем пирамиды V;
2) площадь основания
 ;
3) высоту H,
опущенную из вершины A4
на основание A1A2A3
;
3) высоту H,
опущенную из вершины A4
на основание A1A2A3
278. A1(1; 2; 0), A2 (3; 0; -3), A3 (5; 2; 6), A4 (8; 4; -9)
279. A1(-4; 2; 6), A2 (2; -3; 0), A3 (-10; 5; 8), A4 (-5; 2; -4)
280. A1 (-2; 0; -4), A2 (-1; 7; 1), A3 (4; -8; -4), A4 (1; -4; 6)
281. A1 (5; 2; 0), A2 (2; 5; 0), A3 (1; 2; 4), A4 (-1; 1; 1)
282. A1 (2; -1; 2), A2 (1; 2; -1), A3 (3; 2; 1), A4 (-4; 2; 5)
283. A1 (0; -1; -1), A2 (-2; 3; 5), A3 (1; -5; -9), A4 (-1; -6; 3)
284. A1 (2; 1; 4), A2 (-1; 5; -2), A3 (-7; -3; 2), A4 (-6; -3; 6)
285. A1 (1; 3; 6), A2 (2; 2; 1), A3 (-1; 0; 1), A4 (-4; 6; -3)

. На плоскости даны 3 точки: A(x1; y1), B(x2; y2) и C(x3; y3). Построить треугольник ABC и найти:
1) центр тяжести треугольника О(x0; y0)
2) площадь треугольника SΔ
3) стороны треугольника a, b, c
4) радиус вписанной окружности r и радиус описанной окружности R:
 (результат дать в десятичных дробях)
(результат дать в десятичных дробях)
5) углы треугольника
 A,
A, B,
B, C (результат дать
в градусах)
C (результат дать
в градусах)
6) медианы mA, mB, mC
7) высоты hA, hB, hC
8) биссектрису lA (или lB, или lC)
286. A(-2; 1), B(-6; 4), C(6; 7) 287. A(2; -3), B(-1; -7), C(-6; 3)
288. A(3; 2), B(6; 6), C(8; -10) 289. A(-3; 1), B(5; 7), C(2; -11)
290. A(-1; 5), B(-9; 11), C(3; 6) 291. A(0; 2), B(-6; -6), C(-2; -3)
292. A(3; -3), B(9; 5), C(12; 1) 293. A(2; -1), B(-6; -7), C(-1; 5)
Дополнительные задачи.
294. Дан треугольник ABC : A(1; 0; 2), B(1; 2; 2), C(5; 4; 6). Точка L делит отрезок AC в отношении
1:3, CE - медиана, проведенная из вершины С. Найти координаты точки M пересечения прямых
BL и CE.
295. Дан треугольник ABC : A(1; -1; -3), B(2; 1; -2), C(-5; 2; -6). Найти длину биссектрисы его
внутреннего угла при вершине A.
296. Дан
куб ABCDA1B1C1D1.
Найти косинус угла между векторами
 и
и
 ,
где M - середина
,
где M - середина
ребра DD1.
B1
C1

A1
D1

B
C
M



A
D
297. Выразить площадь треугольника ABC на плоскости через координаты его вершин:
A(x1; y1), B(x2; y2), C(x3; y3).
