Тема 3. Поверхности 2-го порядка.

.

474. Двуполостный гиперболоид с осью OX 475. Однополостный гиперболоид с осью OY 476. Гиперболический цилиндр с образующей, параллельной оси OZ 477. Круговой цилиндр с образующей, параллельной оси OX 478. Эллиптический параболоид с осью OX 479. Параболический цилиндр с образующей, параллельной оси OY 480. Гиперболический цилиндр с образующей, параллельной оси OX 481. Эллиптический параболоид с осью OY 482. Эллипсоид с полуосями: a = 3, b = 6, c = 5 483. Параболический цилиндр с образующей, параллельной оси OX 484. Конус с осью OY и 485. Гиперболический параболоид с осью OY

.

486. а) эллипс в плоскости x = 2 с полуосями a = 2, b = ;

б) эллипс в плоскости y = 0 с полуосями a = 3, b = ;

в) эллипс в плоскости z = 3 с полуосями a = , b =

487. а) сопряженная гипербола в плоскости x = 0 с полуосями a = 3, b = ;

б) эллипс в плоскости y = 1 с полуосями a = , b = ; в) сопряженная гипербола в плоскости z = 5 с полуосями a = 2, b =

488. а) Пустое множество;

б) Парабола z² = 5(x-3)в плоскости y = 3 с вершиной в точке A(3; 3; 0) и с параметром p = 2,5;

в) Парабола y² = 3xв плоскости z = 0 с вершиной в точке A(0; 0; 0) и с параметром p = 1,5

489. а) Парабола z² = - (y - 9)в плоскости x = 3 с вершиной в точке A(3; 9; 0) и с параметром p = 0,5;

б) Пара пересекающихся под углом 90 прямых z = x и z = -x в плоскости y = 0;

в) Парабола x² = - (y - 4)в плоскости z = 2 с вершиной в точке A(0; 4; 2) и с параметром p = 0,5

490. а) Прямая z = -1 в плоскости x = 1, параллельная оси OY;

б) Парабола x² = -z в плоскости y = -5 с вершиной в точке A(0; -5; 0) и с параметром p = 0,5;

в) Пара параллельных оси OY прямых x = 1 и x = -1 в плоскости z = -1

491. а)Пара пересекающихся в начале координат прямых 2y - 3z = 0 и 2y + 3z = 0 в плоскости x = 0;

б) эллипс в плоскости y = 2 с полуосями a = , b = ;

в) сопряженная гипербола в плоскости z = 1 с полуосями a = 2, b =

492. а) Прямая z = 0, параллельная оси OY в плоскости x = 5;

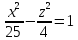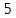б) Гипербола в плоскости y = 0 с полуосями a = , b = ;

в) Пара параллельных оси OY прямых x = и x = - в плоскости z = -1

493. а) Окружность y² z² = 4 в плоскости x = 1 с центром в точке C(1; 0; 0) и радиуса R = 2;

б) Прямая z = 0, параллельная оси OX в плоскости y = 2;

в) Пара параллельных оси OX прямых y = и y = - в плоскости z = 1

.

494. а) Точки пересечения: M₁(2; -3; 0), M₂(0; 0; 2); б) точки пересечения: M₁(3; 4; -2), M₂(6; -2; 2)

495. а) Точка касания: M(4; 2; 9); б) точка касания: M (4; -3; 2)

496. а) y² z² = a²; б) x² z² = 2ax; в) x² y² = 2ax

497. а) (3y - 2z)² = 12(3x - z)²; б) (x - z)² + (y - z)² = 4(x - z) 498. 30

499. а) x² = 2z(y - z + 1); б)

500. а) z = x² y²; б) x⁴ = y² z² 501. а) y² = x² z²; б) z² = x² y²

Найти сторону маленького квадрата и радиусы окружностей, если сторона большого квадрата равна a: