Глава 3. Аналитическая геометрия на плоскости.

Тема 1. Уравнение линии на плоскости.

.

y

y

298. 299.

x

x

1

-1

1

-1

y

y

300. 301.

x

x

3

-2

3

-2

y

y

302. 303.

2

x

-1

x

3

1

y

y

304. 305.

2

1

x

x

1

1

-1

-1

2

-1

y

y

306. 307.

x

1

1

x

1

-1

1

-1

-1

-1

1

y

308. 309.

y

x

x

-1

1

-1

310. 311.

x

y

y

1

-1

x

-2

-1

312. 313.

x

y

y

1

1

-1

-1

1

x

-1

-1

.

y

314. 315.

x

y

1

1

2

-1

x

-3

-1

316. 317.

x

8

y

1

y

1

x

4

1

1

318. 319.

y

y

1

1

x

x

1

-2

-1

320. 321.

8

y

y

4

x

-1

1

-2

x

2

1

1

322. 323.

y

4

y

1

1

x

x

8

2

1

.

y

324.

M

4

а) {1; 2}, M(-2; 4); 1(x + 2) + 2(y - 4) = 0  x + 2y - 6 = 0

x

1

2

-2

6

y

3

б) {-1; 3}, M(2; 1); -1(x - 2) + 3(y - 1) = 0  x - 3y + 1 = 0

x

M

1

2

-1

y

в) {2; -1}, M(-3; 2); 2(x + 3) - 1(y - 2) = 0  2x - y + 8 = 0

M

2

2

-4

x

-3

-1

y

г) {1; 0}, M(-3; -2); 1(x + 3) + 0(y + 2) = 0  x + 3 = 0

-3

x

M

1

-2

y

M

325.

5

а) {1; 2}, M(-3; 5); =  2x - y + 11 = 0

x

1

2

-3

-5,5

y

7

3

б) {-1; 3}, M(2; 1); =  3x + y - 7 = 0

x

M

1

2

-1

y

5

в) {1; -2}, M(3; -1); =  2x + y - 5 = 0

x

3

1

M

-1

-2

y

г) {1; 0}, M(-3; -2); =  y + 2 = 0

-3

x

1

-2

M

326.

y

M

5

а) {1; -2}, M(3; 5);  2x + y - 11 = 0

1

5,5

x

3

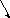
-2

y

3

б) {-1; 3}, M(-2; 1);  3x + y + 5 = 0

x

M

1

-2

-1

-5

y

3

в) {2; 3}, M(1; -1);  3x -2y - 5 = 0

x

2

1

M

-1

-2,5

y

г) {0; 1}, M(-3; 2);  x + 3 = 0

M

1

-3

2

x

327.

y

M₂

5

а) M₁(1; 2), M₂(-3; 5); =  3x + 4y - 11 = 0

2

M₁

x

1

-3

y

3

M₁

б) M₁(-1; 3), M₂(2; -4); =  7x + 3y - 2 = 0

x

2

-1

M₂

-4

y

в) M₁(1; -2), M₂(1; 2); =  x -1 = 0

x

M₂

1

2

-2

M₁

-1

y

1

M₂

г) M₁(-1; -2), M₂(3; 1); =  3x - 4y - 5 = 0

x

M₁

3

-2

328.

y

а) a = 4, b = 3; + = 1  3x + 4y - 12 = 0

3

x

4

y

б) a = -3, b = 2; + = 1  2x - 3y + 6 = 0

x

2

-3

y

в) a = 1, b = - 4; 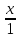+ = 1  4x - y - 4 = 0

x

1

-4

y

г) a = -2, b = -3; + = 1  3x + 2y + 6 = 0

x

-2

-3

329.

y

а) = 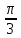, p = 4; xcos + ysin 4 = 0  x + y - 8 = 0

4

x

8

y

3

б) = , p = 3; xcos + ysin 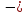3 = 0  x + y - 3 = 0

x

3

3

y

4

в) = , p = 2; xcos + ysin 2 = 0  x - y + 4 = 0

x

2

y

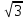г) = - , p = ; xcos + ysin = 0 

x

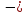
 x + y + 2 = 0

-2

y

330.

M

а) = , M(-3; 5); y - 5 = tg (x + 3) 

5

 x - y + 5 + 3 = 0

x

-3

y

б) = , M(1; -2); y + 2 = tg 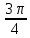(x - 1)  x + y + 1 = 0

x

1

-2

M

y

в) = , M(2; 1); y - 1 = tg (x - 2)  x - y + 1 - 2 = 0

x

1

M

2

3

y

г) = , M(0; 3); y - 3 = tg (x - 0)  x - y + 3 = 0

M

x

y

331.

а) y₀ = 1  y - 1 = 0

1

x

y

б) x₀ = 4  x - 4 = 0

x

4

y

в) x₀ = -3  x + 3 = 0

-3

y

г) y₀ = -2  y + 2 = 0

x

-2

.

332. [AB]: 3x + 4y + 2 = 0, [AC]: 3x - 4y + 10 = 0, [BC]: x - 4y + 22 = 0,

[m_A]: 9x - 4y + 22 = 0, [h_A]: 4x + y + 7 = 0, [l_A]: x + 2 = 0.

333. [AB]: 4x - 3y - 6 = 0, [AC]: 12x + 5y - 46 = 0, [BC]: 8x + y - 54 = 0,

[m_A]: x + y - 5 = 0, [h_A]: x - 8y + 13 = 0, [l_A]: x + 8y - 19 = 0.

334. [AB]: 3x - 4y + 13 = 0, [AC]: 12x + 5y + 31 = 0, [BC]: 6x - y - 23 = 0,

[m_A]: 6x + 13y + 5 = 0, [h_A]: x + 6y - 3 = 0, [l_A]: 3x + 11y - 2 = 0.

335. [AB]: 4x - 3y + 6 = 0, [AC]: 3x - 4y - 6 = 0, [BC]: 5x - 2y + 4 = 0,

[m_A]: 11x - 10y + 6 = 0, [h_A]: 2x + 5y + 42 = 0, [l_A]: x - y = 0.

336. [AB]: x - y = 0, [AC]: x - 7y = 0, [BC]: x + 5y - 12 = 0,

[m_A]: x - 3y = 0, [h_A]: 5x - y = 0, [l_A]: x - 2y = 0.

337. [AB]: x + 2y + 4 = 0, [AC]: 2x - 11y - 7 = 0, [BC]: 4x - 7y - 29 = 0,

[m_A]: y + 1 = 0, [h_A]: 7x + 4y + 18 = 0, [l_A]: x + 7y + 9 = 0.