9 Правило Лопиталя раскрытия неопределенностей

Элементарные способы нахождения предела функции иногда оказываются трудоемкими. В ряде случаев целесообразно использовать правило Лопиталя.

Пусть в некоторой окрестности и точки (кроме, быть может, самой точки ) функции и дифференцируемы и . Если или , т.е частное в точке представляет собой неопределенность вида или , то , если предел в правой части этого равенства существует. Другими словами, суть правила Лопиталя состоит в том, что для неопределенностей вида или вычисление предела отношения функций, можно заменить, при соблюдении указанных требований,

вычислением предела отношения их производных, что в большинстве случаев значительно проще.

Если предел отношения производных снова приводит к одному из указанных неопределенностей, то можно применить правило Лопиталя еще раз, т.е исследовать отношение вторых производных и т.д. При этом, прежде чем исследовать отношение вторых, третьих и т.д. производных, нужно максимально упростить выражения, полученные на предыдущем этапе.

В случае неопределенности вида или следует алгебраически преобразовать данную функцию так, чтобы привести ее к неопределенности или и далее воспользоваться правилом Лопиталя. В случае неопределенности вида или или следует прологарифмировать данную функцию и найти предел ее логарифма. В ряде случаев целесообразно сочетать правило Лопиталя с приемами вычисления пределов рассмотренными в пунктах 3-8.

Пример 13. Найти

Решение.

=

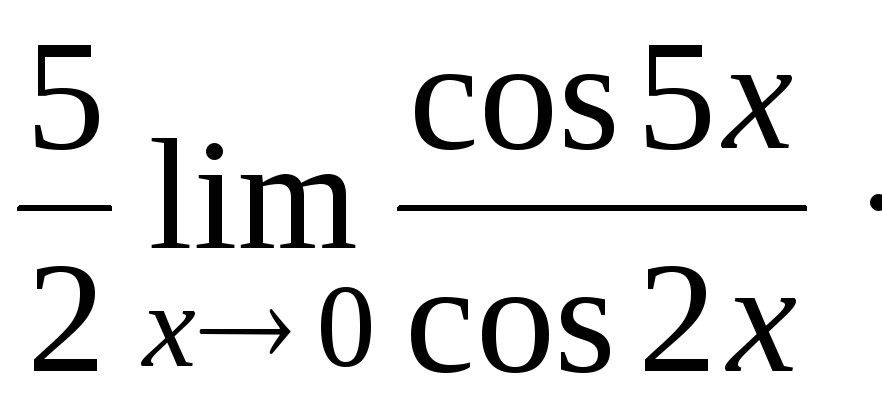
Здесь правило Лопиталя применили два раза.

Пример 14. Найти

Решение.

=

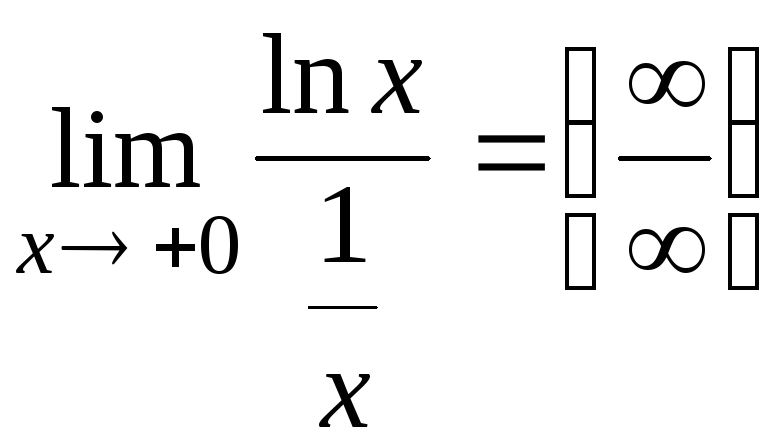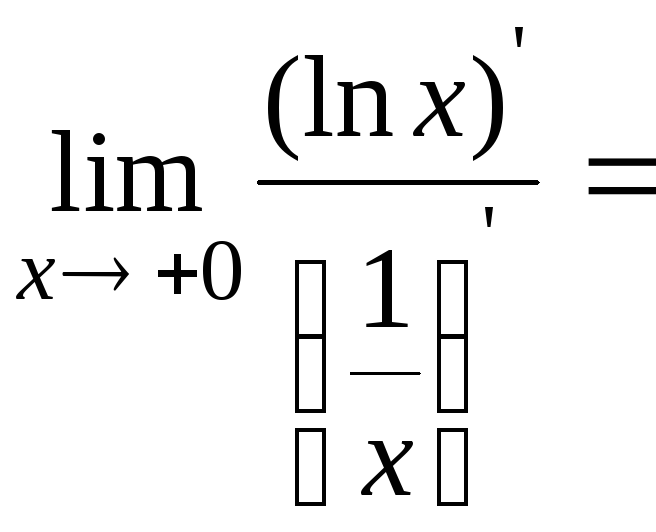
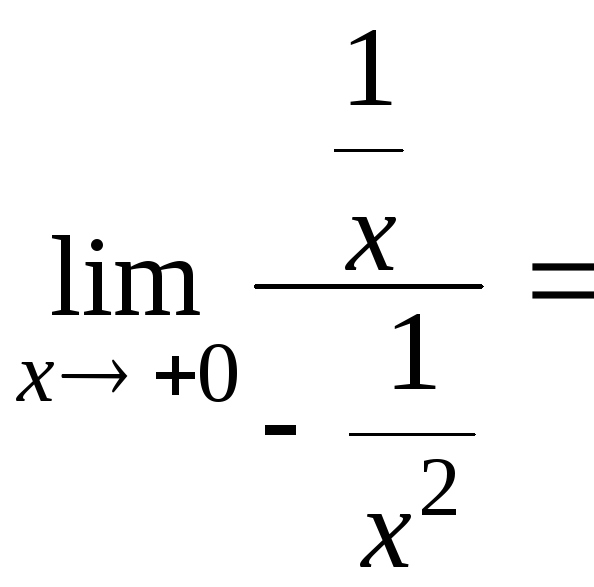
Пример 15. Найти

Решение.

=

=

Пример 16. Найти

Решение.

Сначала устанавливаем, что имеет место случай . Затем логарифмируем функцию и ищем предел ее логарифма.

=

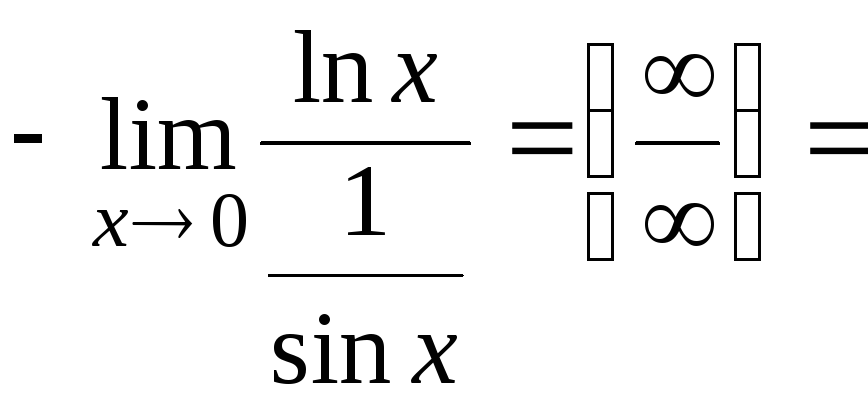
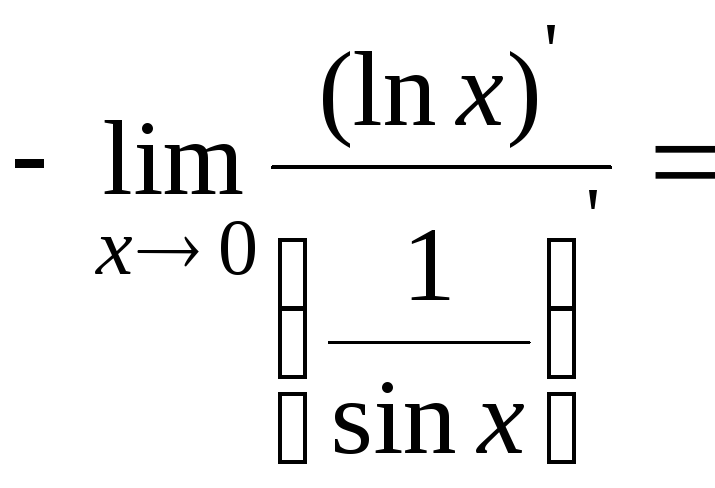
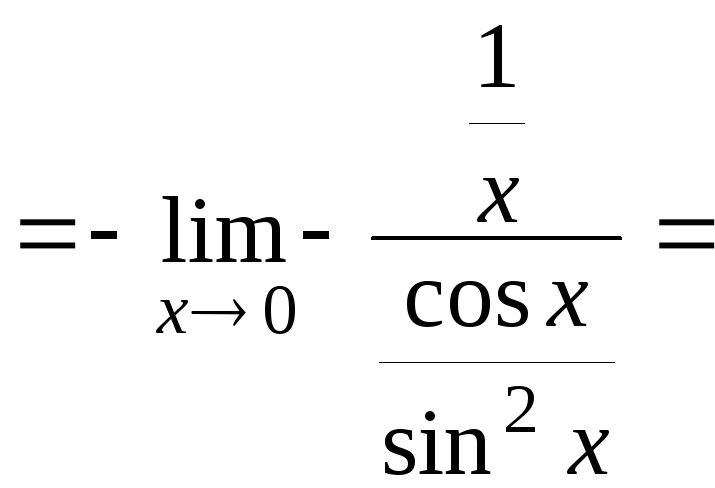
Итак

Библиография

1. Кудрявцев В.А., Демидович Б.И. Краткий курс высшей математики.-М: Наука, 1986.-576с.

2. Пискунов Н.С. Дифференциальное и интегральное исчисление. Том I-М.: Наука, 1978.-456с.

3. Минорский В.И. Сборник задач по высшей математике.-М.: Наука, 1987.-352с.

4. Шипачев В.С. Сборник задач по высшей математике.-М.: Высшая школа,1998.-352с.

Приложение А

Расчетные задания

Задача 1. Доказать, что (указать ).

1.1 ,

1.2 ,

1.3 ,

1.4 ,

1.5 ,

1.6 ,

1.7 ,

1.8 ,

1.9 ,

1.10 ,

1.11 ,

1.12 ,

1.13 ,

1.14 ,

1.15 ,

1.16 ,

1.17 ,

1.18 ,

1.19 ,

1.20 ,

Продолжение приложения А

Задача 2. Вычислить пределы числовых последовательностей.

2.1

2.2

2.3

2.4

2.5

2.6

2.7

2.8

2.9

2.10

2.11

2.12

2.13

2.14

2.15

2.16

2.17

2.18

2.19

2.20

Продолжение приложения А

Задача 3. Вычислить пределы числовых последовательностей.

3.1

3.2

3.3

3.4

3.5

3.6

3.7

3.8

3.9

3.10

3.11

3.12

3.13

3.14

3.15

3.16

3.17

3.18

3.19

3.20

Продолжение приложения А

Задача 4. Вычислить пределы числовых последовательностей.

4.1

4.2

4.3

4.4

4.5

4.6

4.7

4.8

4.9

4.10

4.11

4.12

4.13

4.14

4.15

4.16

4.17

4.18

Продолжение приложения А

4.19

4.20

Задача 5. Вычислить пределы числовых последовательностей.

5.1

5.2

5.3

5.4

5.5

5.6

5.7

5.8

5.9

5.10

5.11

5.12

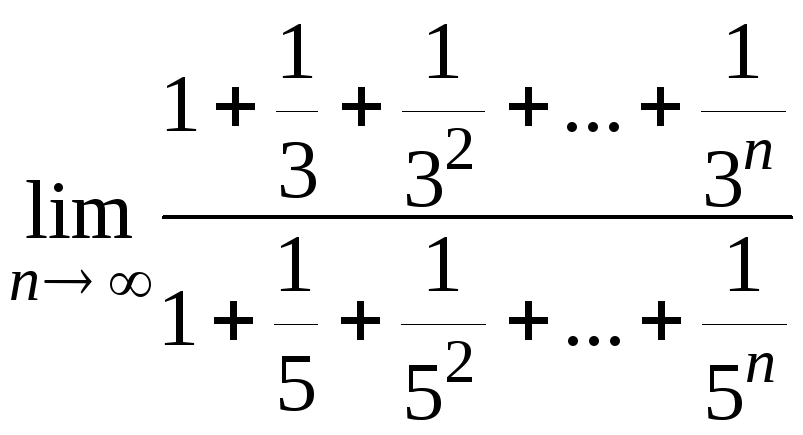
5.13

Продолжение приложения А

5.14

5.15

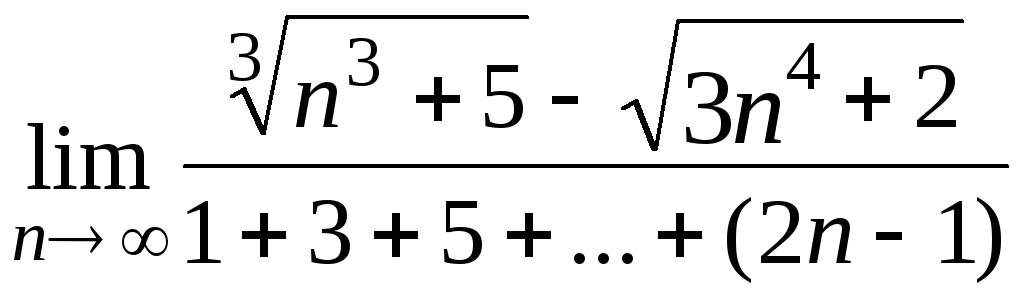
5.16

5.17

5.18

5.19

5.20

Задача 6. Доказать (найти , что:

6.1

6.2

6.3

6.4

6.5

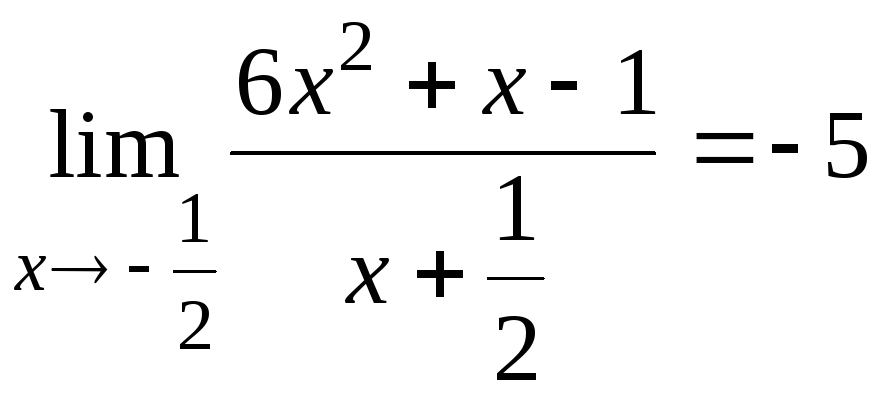
6.6

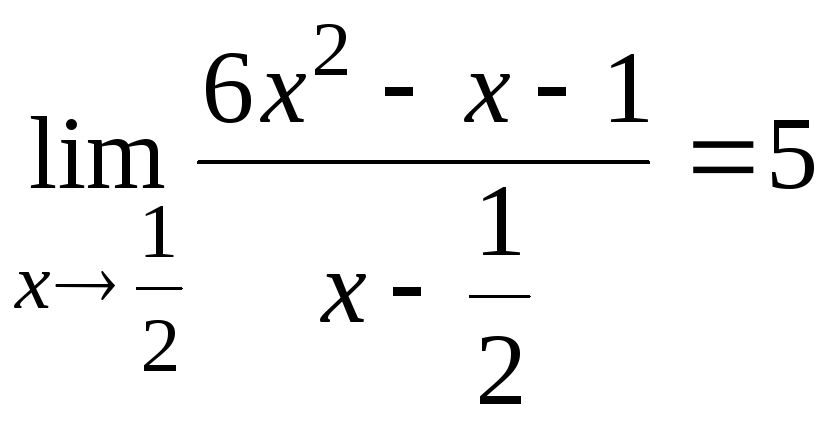
6.7

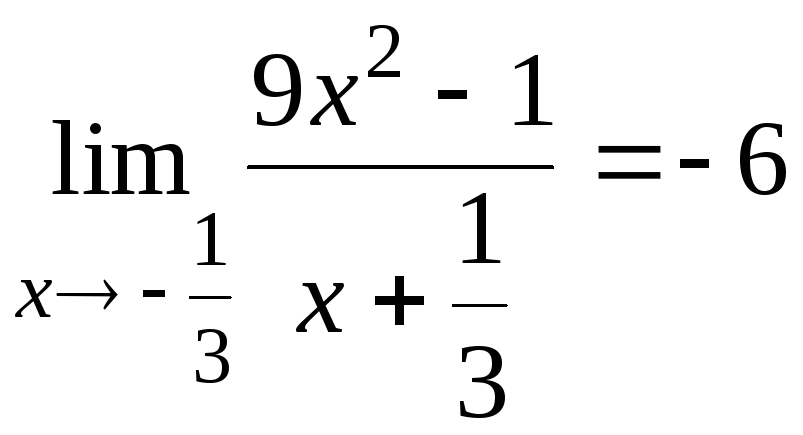
6.8

Продолжение приложения А

Продолжение приложения А А

6.9

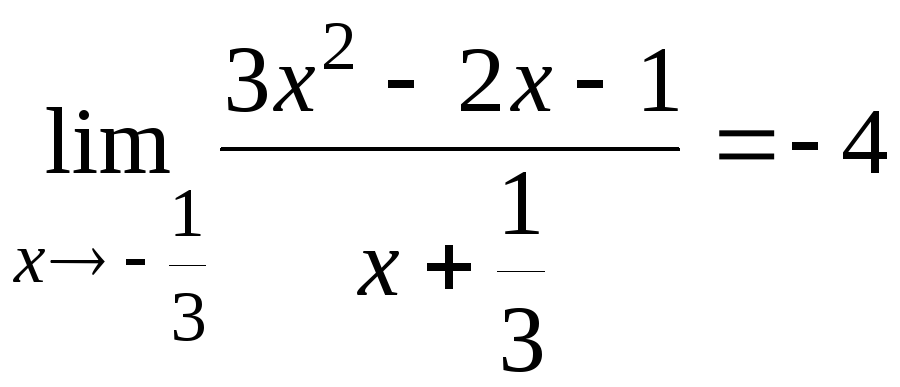
6.10

6.11

6.12

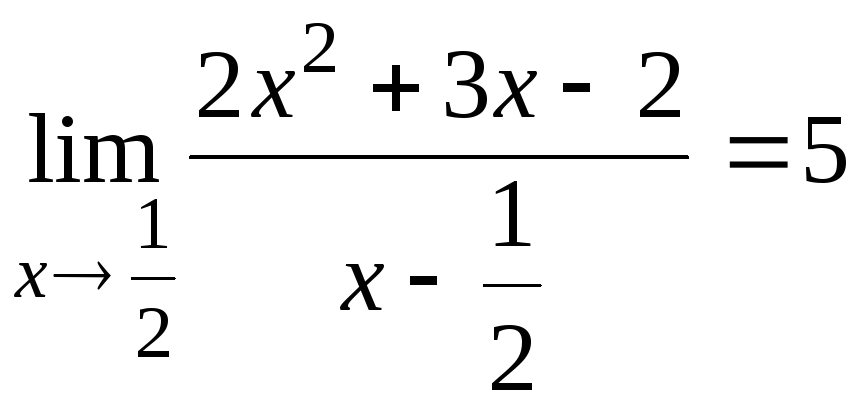
6.13

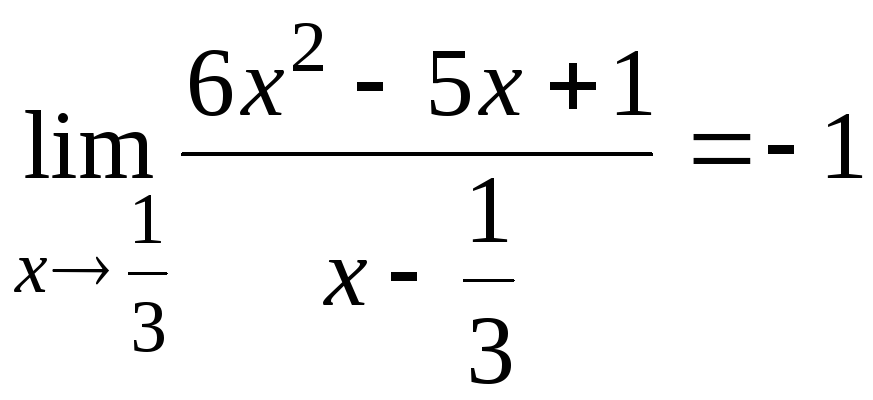
6.14

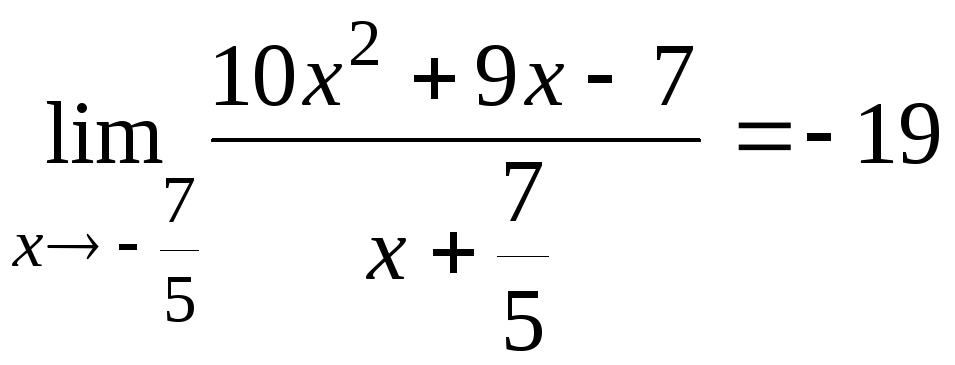
6.15

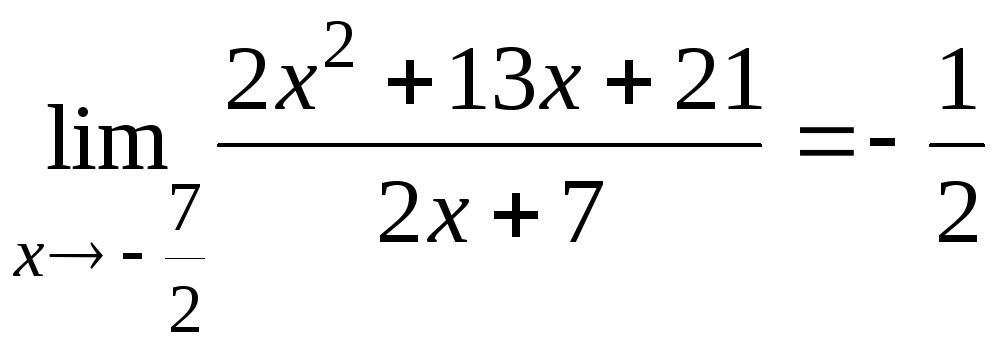
6.16

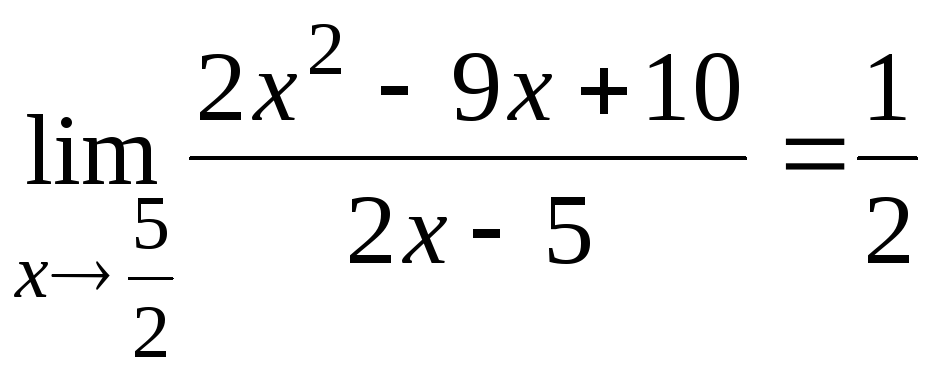
6.17

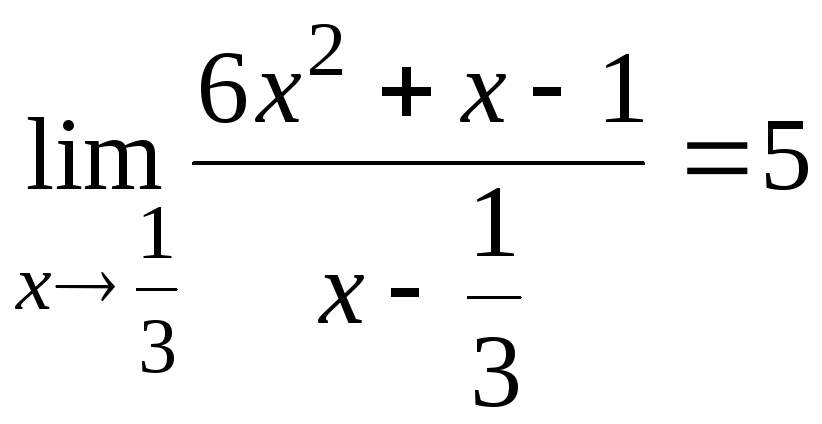
6.18

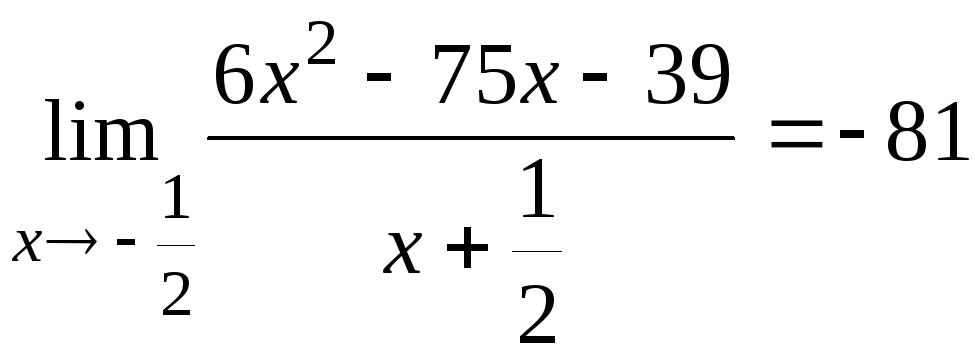
6.19

6.20

Задача 7. Вычислить пределы функций.

7.1

7.2

7.3

7.4

7.5

7.6

7.7 7.8

7.9

7.10

Продолжение приложения А

7.11

7.12

7.13

7.14

7.15

7.16

7.17

7.18

7.19

7.20

Задача 8. Вычислить пределы функций.

8.1

8.2

8.3

8.4

8.5

8.6

8.7

8.8

8.9

8.10

8.11

8.12

Продолжение приложения А

8.13

8.14

8.15

8.16

8.17

8.18

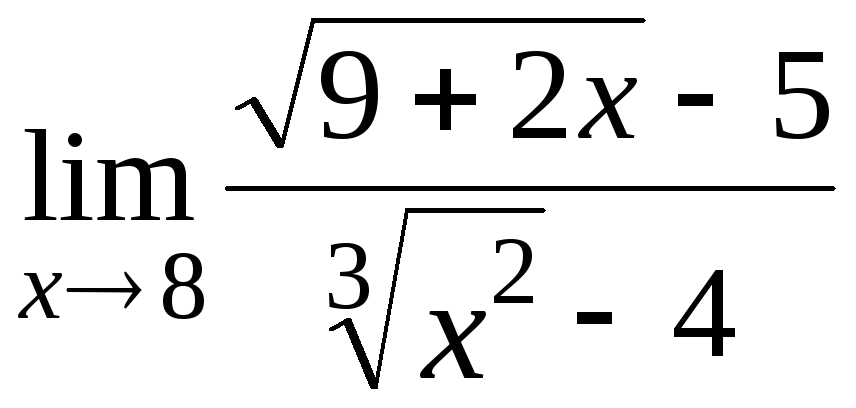
8.19

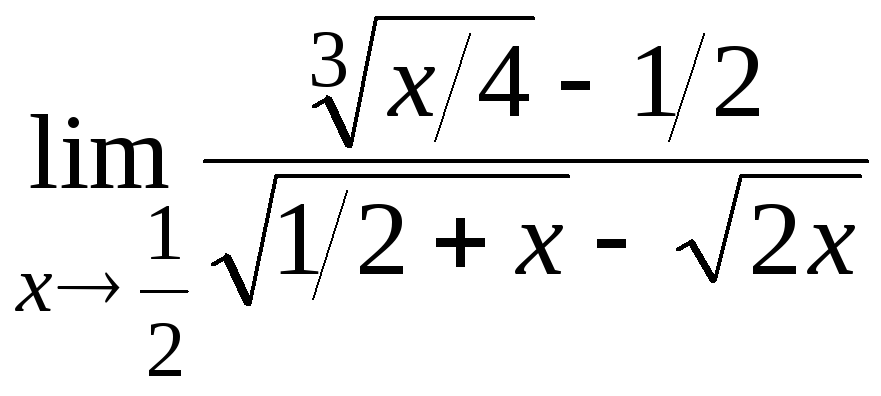
8.20

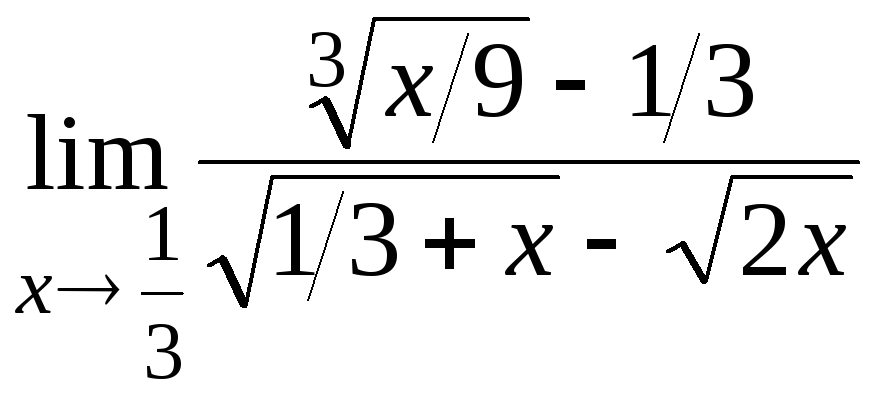
Задача 9. Вычислить пределы функций.

9.1

9.2

9.3

9.4

9.5

9.6

9.7

9.8

9.9

9.10

9.11

9.12

9.13

9.14

Продолжение приложения А

9.15

9.16

9.17

9.18

9.19

9.20

Задача 10. Вычислить пределы функций.

10.1

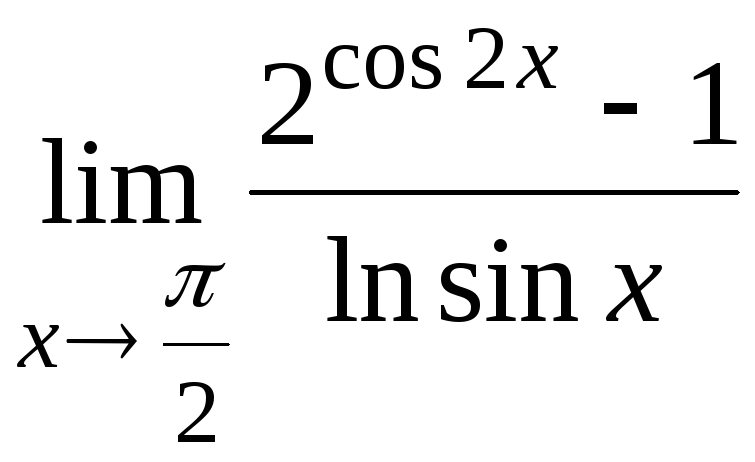
10.2

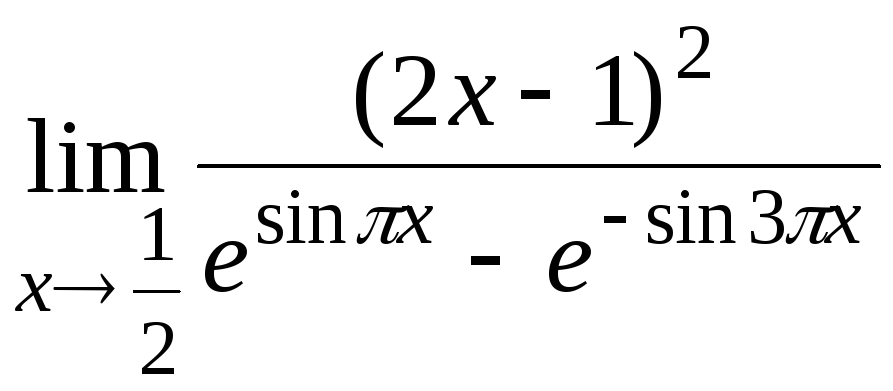
10.3

10.4

10.5

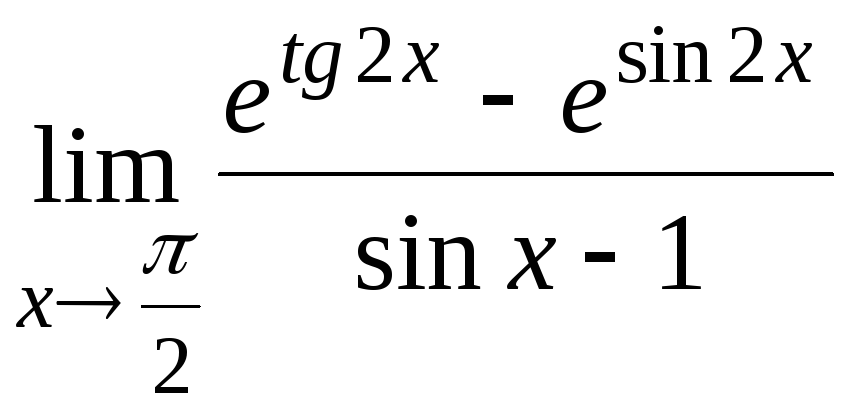
10.6

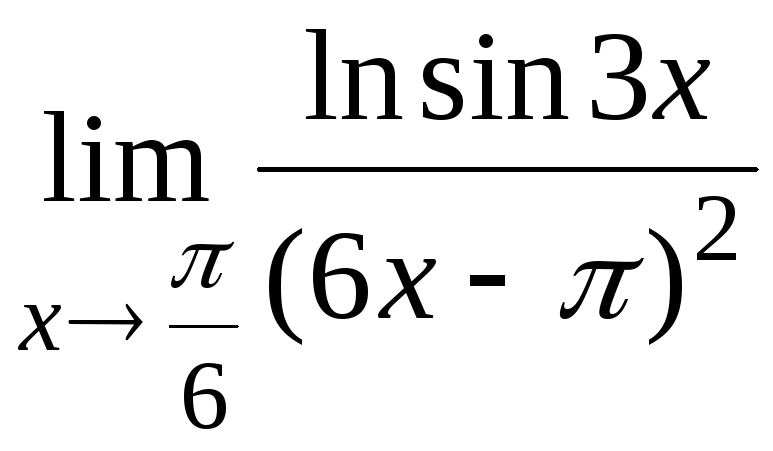
10.7

10.8

10.9

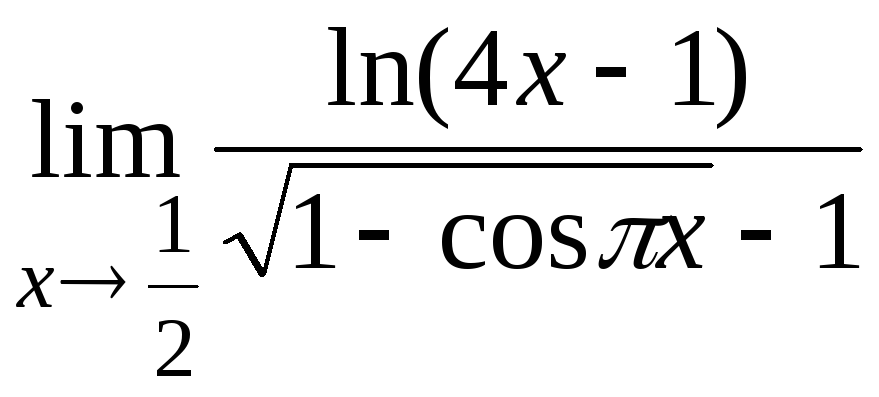
10.10

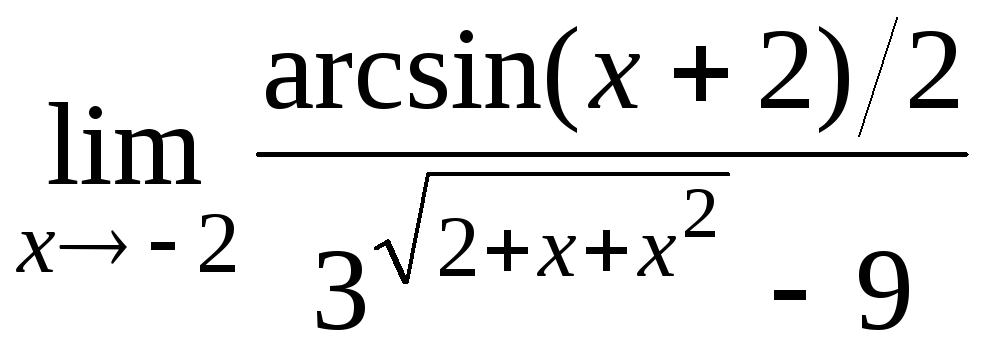
10.11

10.12

10.13

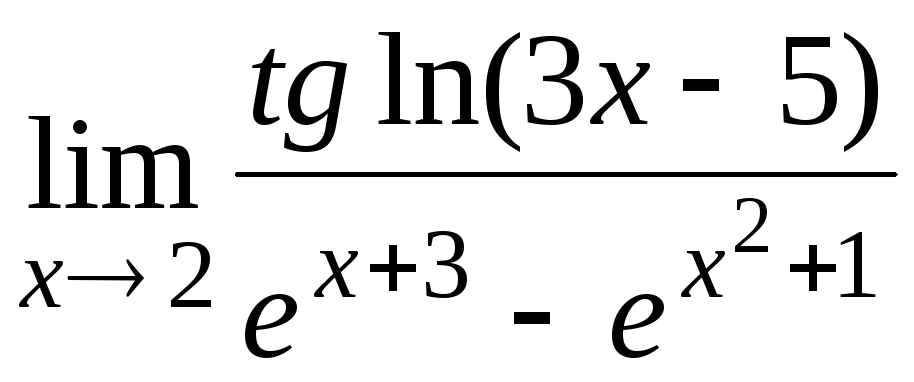
10.14

Продолжение приложения А

10.15

10.16

10.17

10.18

10.19

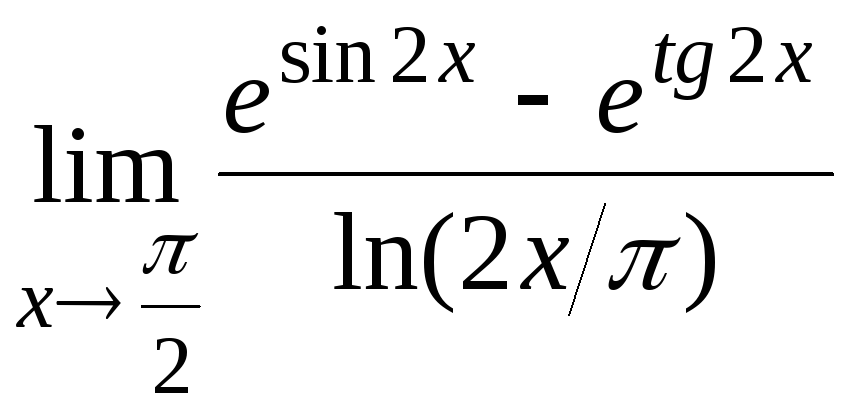
10.20

Задание 11. Вычислить пределы функций.

11.1

11.2

11.3

11.4

11.5

11.6

11.7

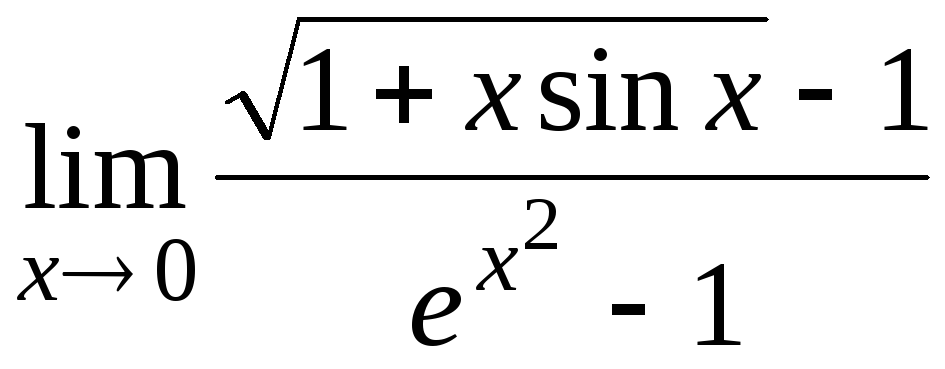
11.8

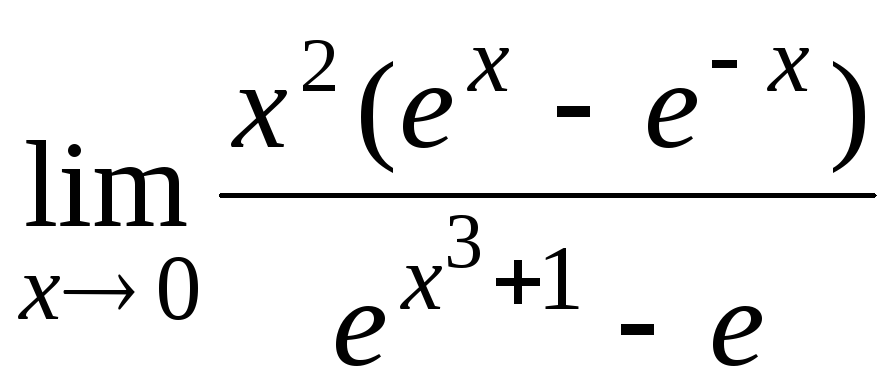
11.9

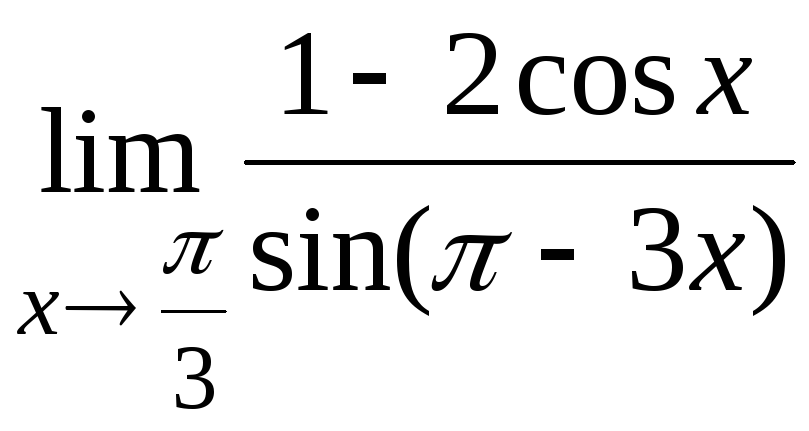
11.10

11.11

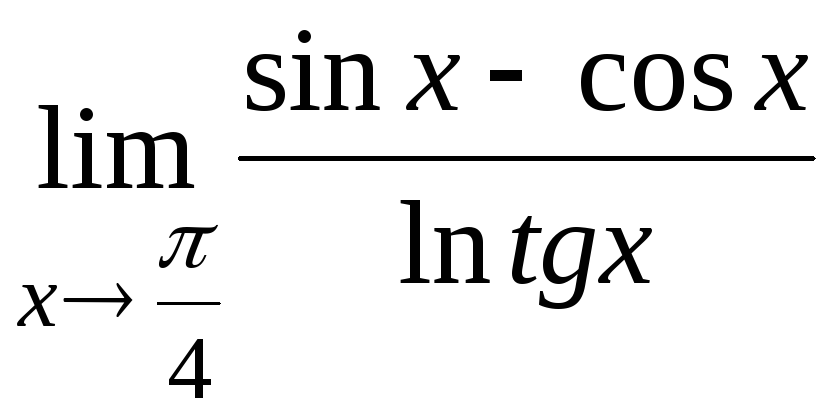
11.12

11.13

11.14

Продолжение приложения А

11.15

11.16

11.17

11.18

11.19

11.20

Задача 12. Вычислить пределы функций.

12.1

12.2

12.3

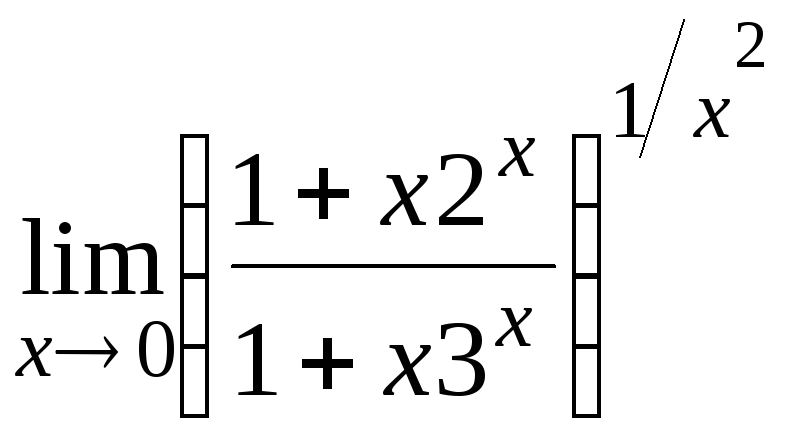
12.4

12.5

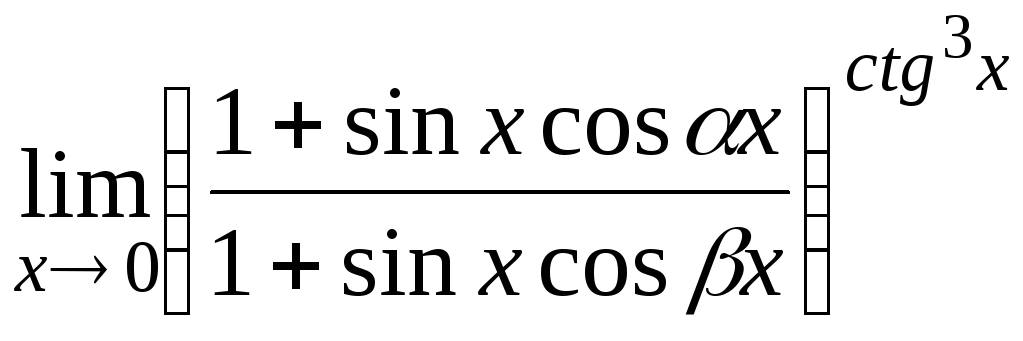
12.6

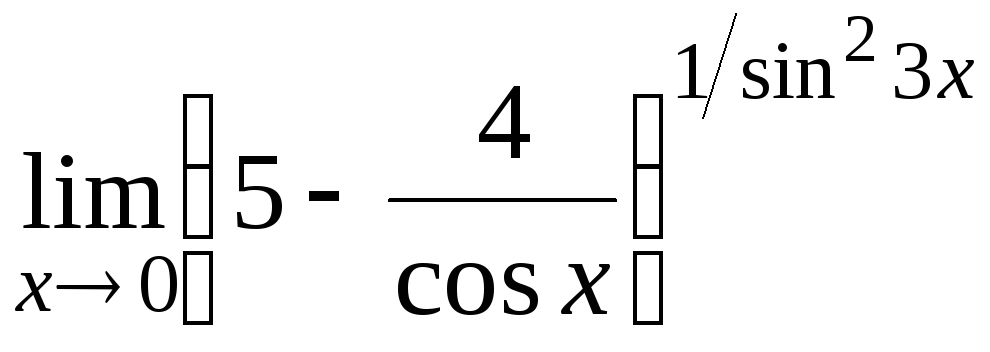
12.7

12.8

12.9

12.10

12.11

12.12

12.13

12.14

12.15

12.16

12.17

12.18

Продолжение приложения А

12.19

12.20

Задача 13. Вычислить пределы функций.

13.1

13.2

13.3

13.4

13.5

13.6

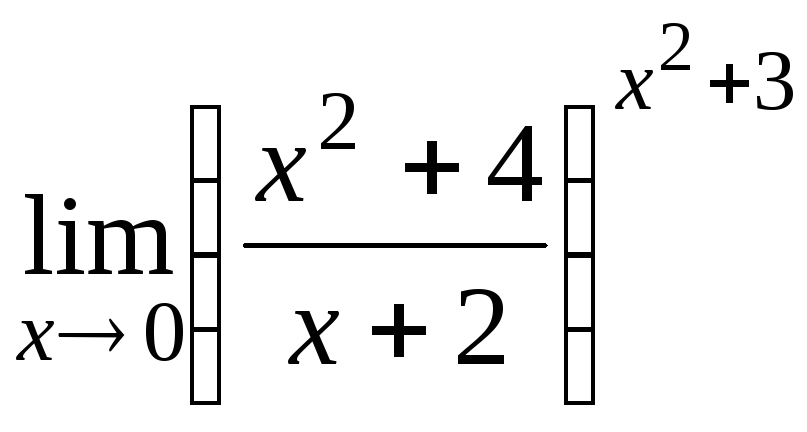
13.7

13.8

13.9

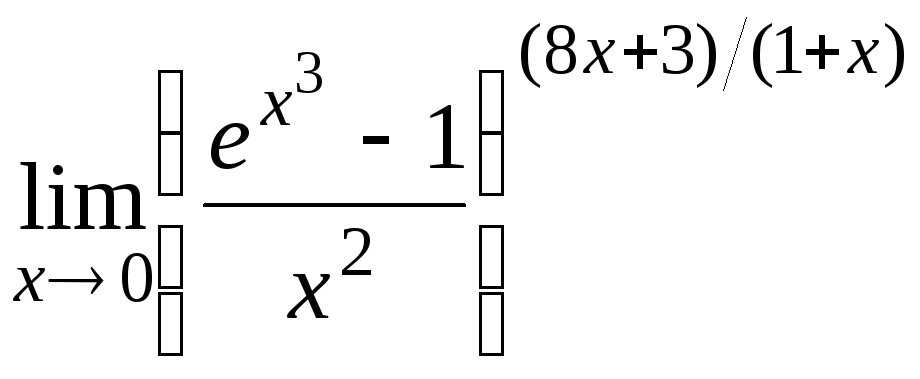
13.10

13.11

13.12

13.13

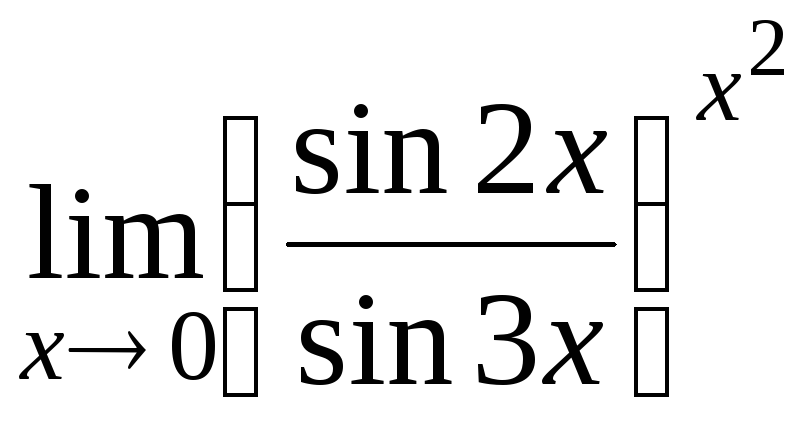
13.14

13.15

13.16

13.17

13.18

Продолжение приложения А

13.19

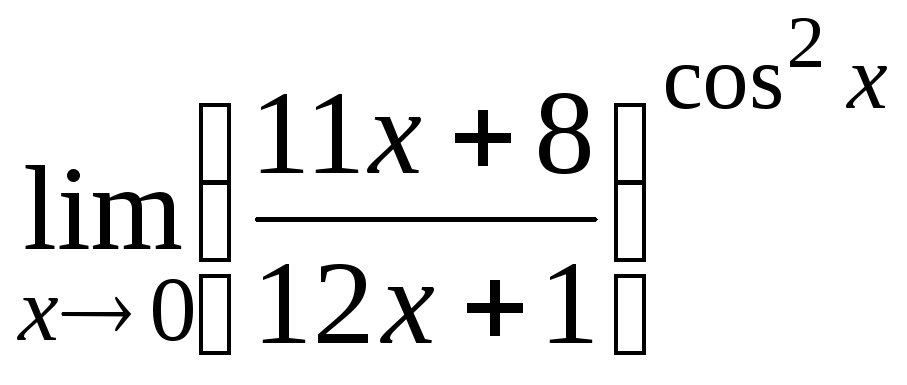
13.20

Задача 14. Вычислить пределы функций.

14.1

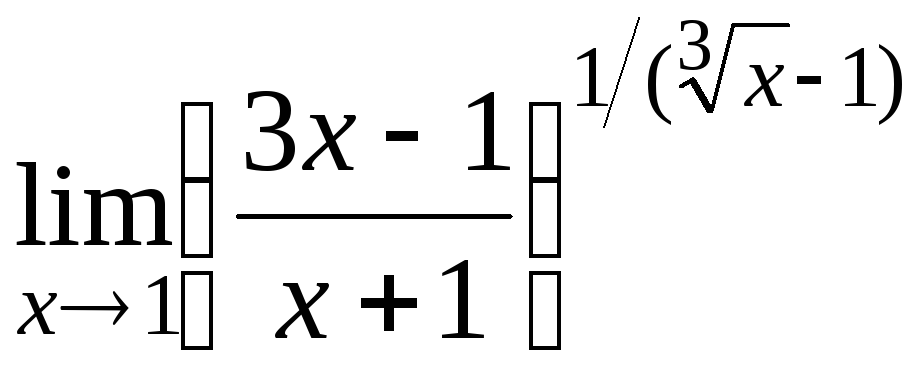
14.2

14.3

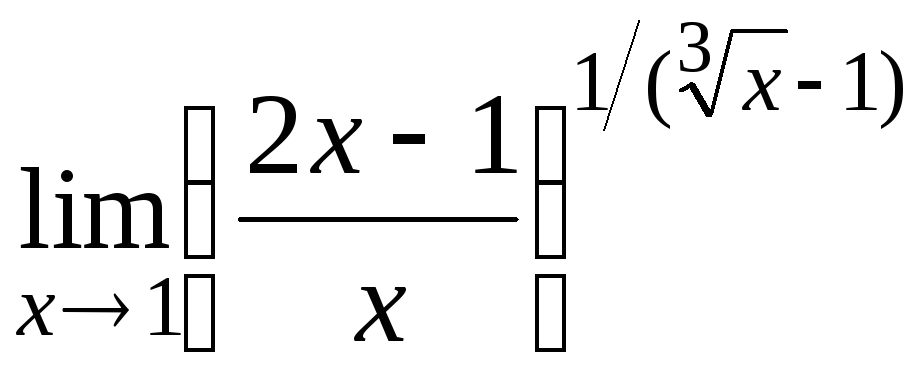
14.4

14.5

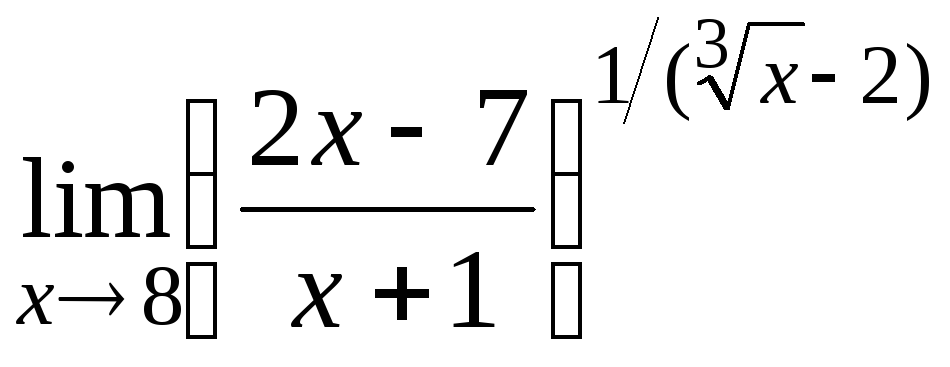
14.6

14.7

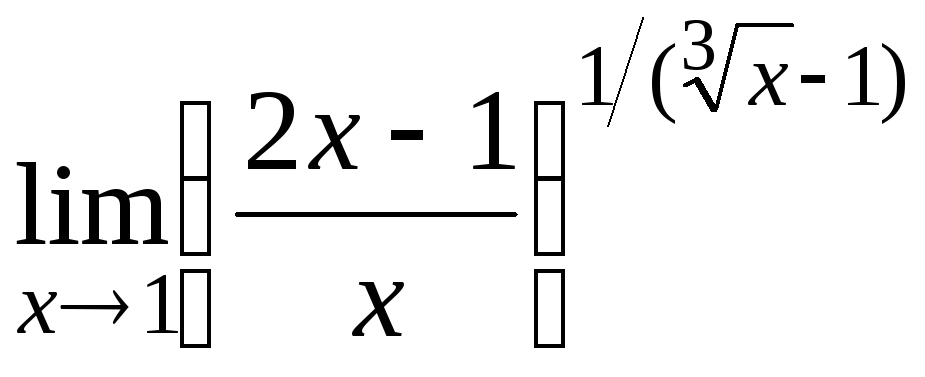
14.8

14.9

14.10

14.11

14.12

14.13

14.14

14.15

14.16

Продолжение приложения А

14.17

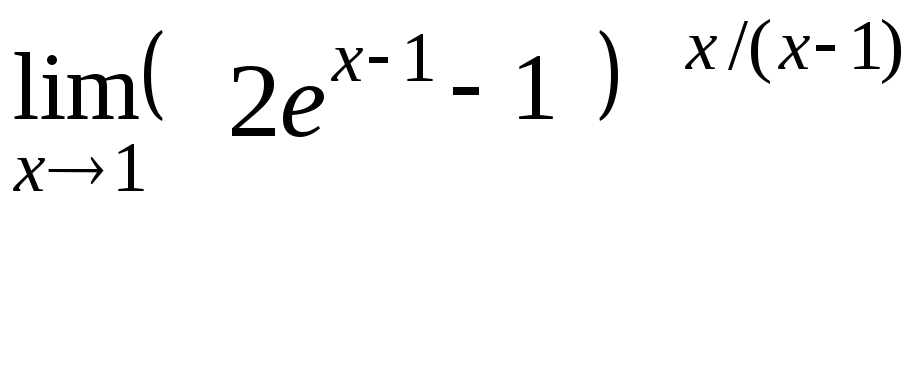
14.18

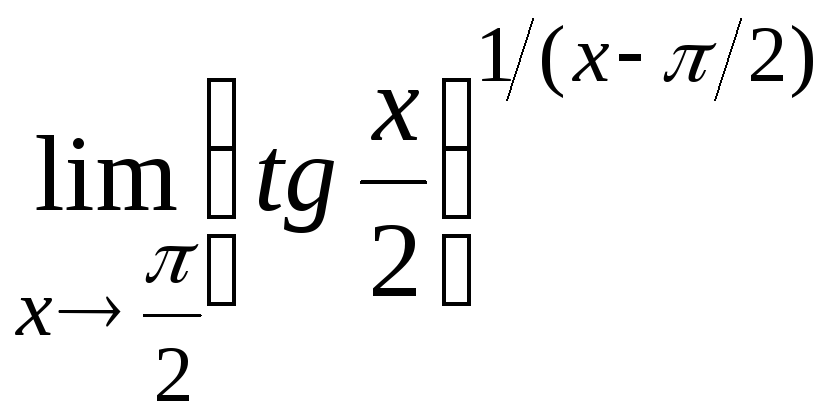
14.19

14.20

Задача 15. Вычислить пределы функций.

15.1

15.2

15.3

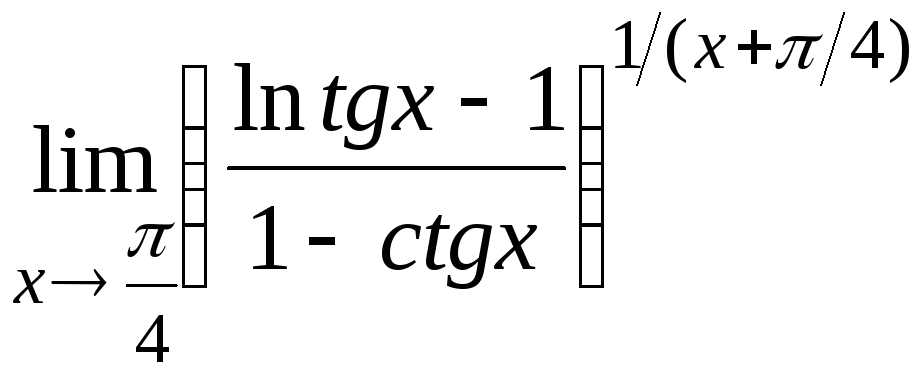
15.4

15.5

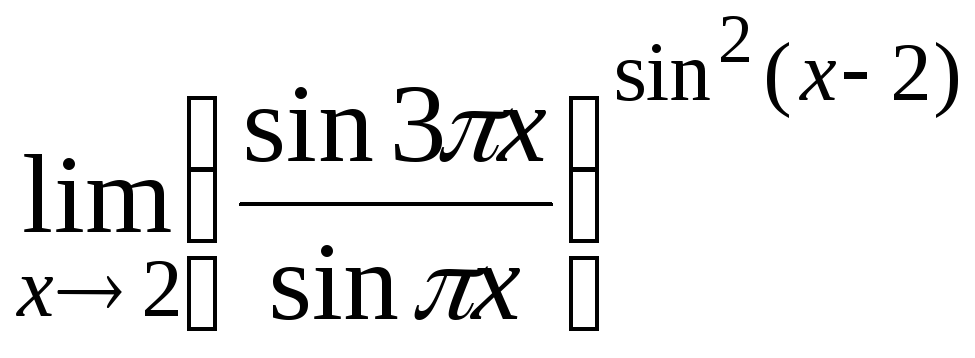
15.6

15.7

15.8

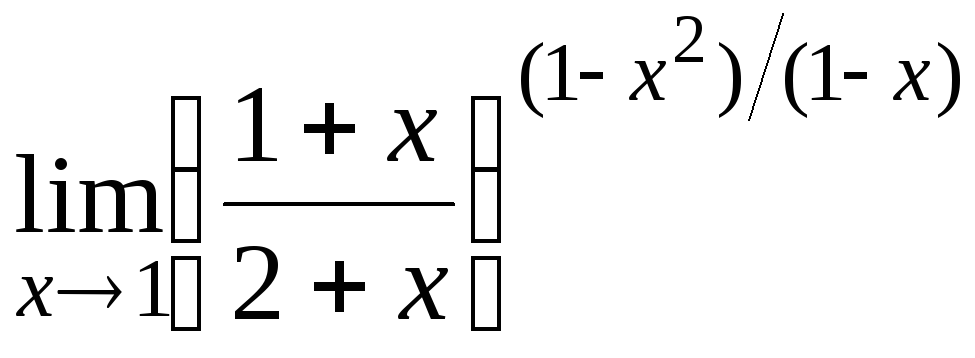
15.9

15.10

15.11

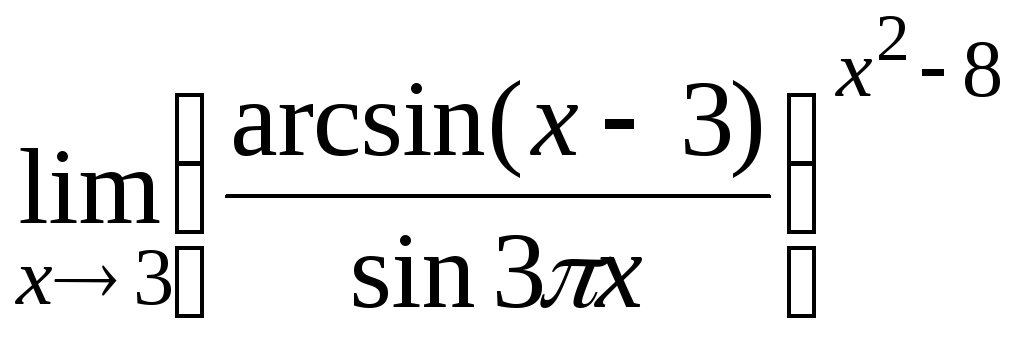
15.12

15.13

15.14

Продолжение приложения А

15.15

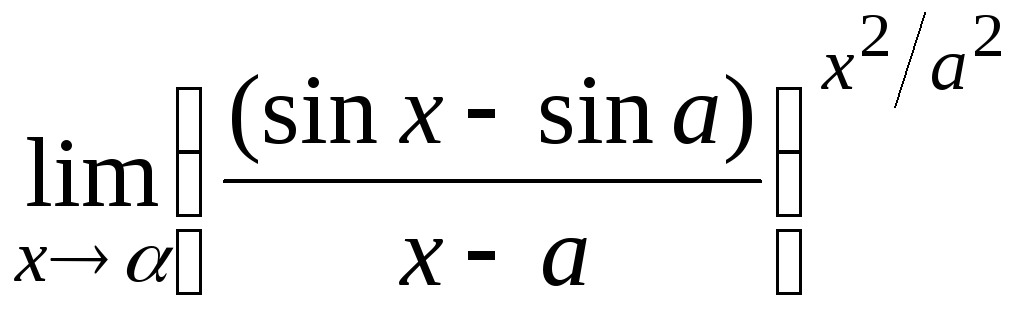
15.16

15.17

15.19

15.18

15.20