18

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ»

Кафедра математики

Методические указания

и задания к расчетно-графической работе по теме:

Пределы последовательностей и функций

для студентов всех специальностей

Уфа 2010

УДК 378.147.88:517

ББК 74.58:22.1

М 54

Рекомендовано к изданию методической комиссией Факультета

механизации сельского хозяйства

(протокол № 2010 год)

Составители:

ст. преподаватель О.В. Захарова

доцент Э.Ф. Калимуллина

Рецензент:

доцент кафедры теоретической и прикладной механики

Р.Г. Ахмаров

Ответственный за выпуск:

зав. кафедрой математики

Р.Л. Лукманов

Введение

Цель настоящих методических указаний - оказать помощь студентам в самостоятельном изучении темы «Пределы последовательностей и функций», выполнении расчетно-графической работы, подготовке к экзамену или зачету. В соответствии с этим, в указаниях приводятся некоторые теоретические сведения, показано решение типичных примеров. В конце методических указаний имеются варианты расчетно-графических заданий по теме «Пределы последовательностей и функций», которые могут быть использованы на всех факультетах БГАУ.

Все задачи расчетно-графической работы разбиты на 15 серий. Студент группы номер l,имеющий вариант i из серии номер k, решает задачу, номер которой определяется последней строкой таблицы, которая заполняется следующим образом. В первой строке таблицы записаны номера серий. Во второй - записаны значение выражения i+lk, а в третьей - номер задачи из k-той серии, который равен числу i+lk, если оно не превосходит 20, и остатку от деления этого числа на 20,в противном случае. Заполним, к примеру, таблицу при l=3 (3 группа) и i=14 (14 вариант)

Таблица. Выбор варианта.

k	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
i+lk	17	20	23	26	29	32	35	38	41	44	47	50	53	56	59
Номер задачи в серии	17	20	3	6	9	12	15	18	1	4	7	10	13	16	19

1 Некоторые теоретические сведения

Число называется пределом последовательности x₁,х₂,…,x_n , если для всякого сколь угодно малого положительного числа найдется такое положительное число N, что при . В этом случае пишут: .

Число А называется пределом функции при , если для любого сколь угодно малого найдется такое , что при

. Это записывают так:

Аналогично , если при .

Условно записывают , если при , где М - произвольное положительное число. В этом случае функция называется бесконечно большой при .

Если , то функция называется бесконечно малой при .

Практическое вычисление пределов основывается на следующих теоремах.

Если существуют и , то

1) ;

2) ;

3)

4) 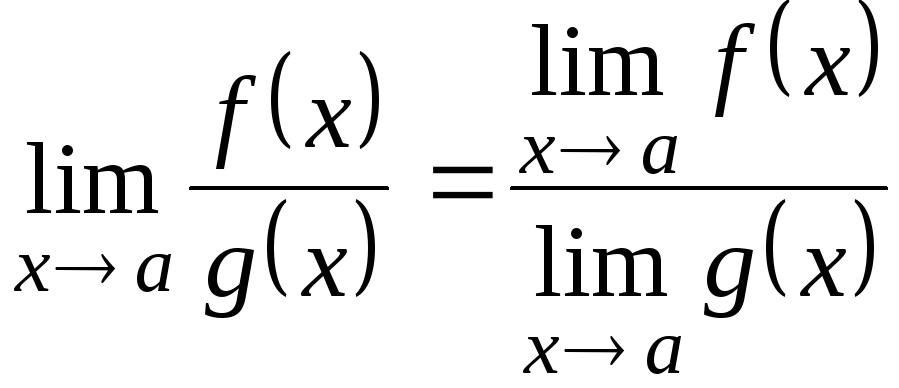(при ).

Путем элементарных рассуждений, основанных на свойствах пределов, можно получить следующие наиболее часто встречающиеся пределы (постоянная ):

1) 2)

3) 4)

5) 6)

7)

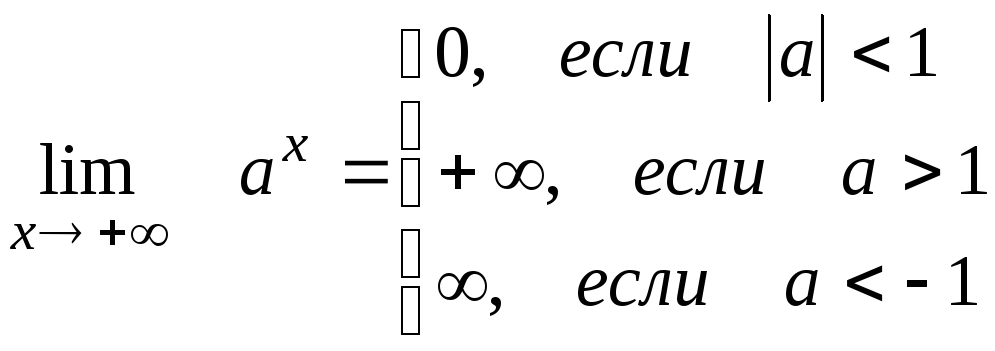
8)

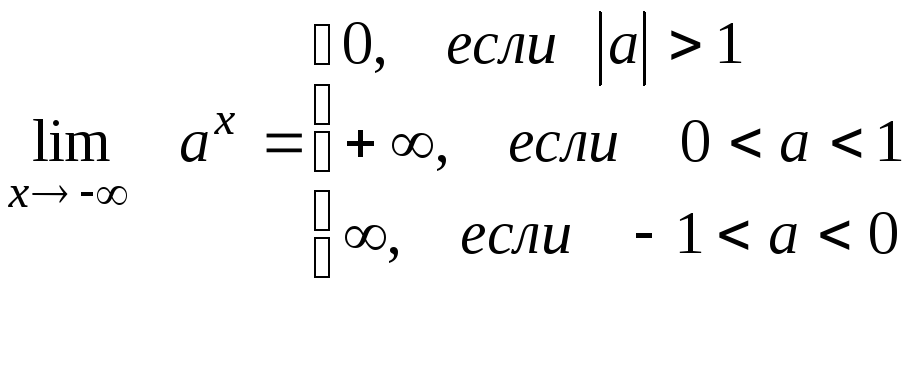
Замечание: В пунктах 7, 8 при переменная может принимать только целочисленные значения, для всех значений при функция не определена

9)

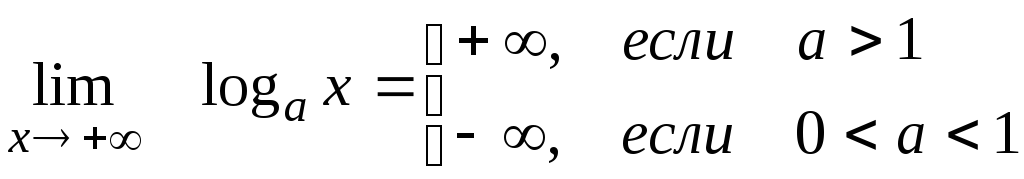
10)

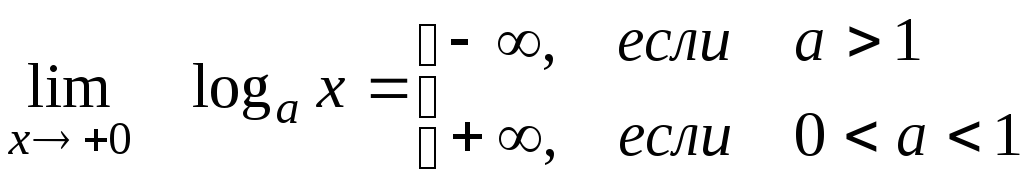
Используются также следующие пределы:

(первый замечательный предел);

(второй замечательный предел)

Функция называется непрерывной в точке , если:

1) эта функция определена в некоторой окрестности и точки ;

2) существует предел ;

3) этот предел равен значению функции в точке , т.е. .

При нахождении пределов часто используется тот факт, что все основные

элементарные функции непрерывны при всех значениях x, для которых они определены.