Задача к4

Дано: , , , , , AD=DB, , , , l₄ = 0,6 м, , (направления – против хода часовой стрелки).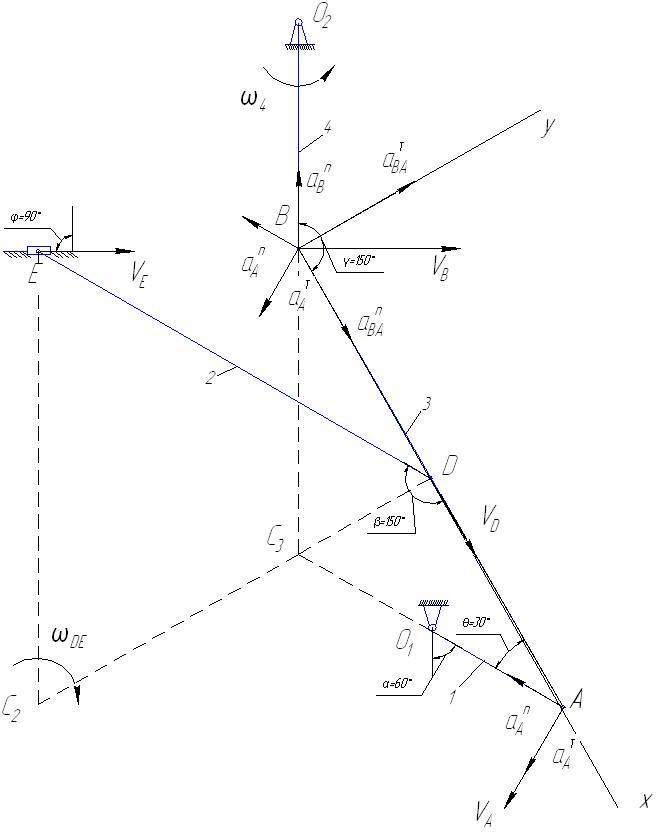

Определить: V_A, V_E, _DE, a_A, _BA.

Решение. 1. Строим положение механизма в соответствии с заданными углами и длинами стержней.

2. Определяем V_A. Точка A принадлежит стержню 1, совершающему вращательное движение, т.е. и стержню 3. Чтобы найти 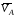, нужно знать направление и скорость другой точки звена 3. Такой точкой является точка В, принадлежащая еще звену 4 (звено вращается вокруг О₂).

V_В = ₄l₄ = 3 м/c; . (1)

Направление найдем, учитывая, что направления – против хода часовой стрелки. Теперь воспользуемся теоремой о проекциях скоростей двух точек тела (стержня 3) на прямую, соединяющую эти точки (прямая AB). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор (проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим

и V_А = 3 м/c. (2)

3. Определяем . Точка Е принадлежит стержню 2, совершающему плоскопараллельное движение. Чтобы определить , надо сначала найти скорость точки D, принадлежащей одновременно стержню 3. Для этого, зная и , строим мгновенный центр скоростей (МЦС) стержня АВ; это точка C₃, лежащая на пересечении перпендикуляров к и , восставленных из точек A и B. По направлению вектора определяем направление мгновенного поворота стержня 3 вокруг МЦС C₃. Вектор перпендикулярен отрезку C₃D, соединяющему точки D и C₃, и направлен в сторону мгновенного поворота тела. Величину V_D найдем из пропорции

. (3)

Чтобы вычислить C₃D и С₃B, заметим, что AC₃B – равносторонний, так как острые углы в нем равны 30°, и что . BC₃D является прямоугольным и С₃D=C₃B·cos60°=0,81·0,5=0,405. В результате равенство (3) дает

; . (4)

Направление найдем, учитывая, что точка E принадлежит одно­временно ползуну, движущемуся вдоль направляющих поступательно. В точках Е и D построим перпендикуляры к скоростям и , получим точку С₂ – МЦС стержня 2. По направлению вектора определяем направление мгновенного поворота стержня 2 вокруг центра С₂. Вектор направлен в сторону поворота этого стержня. Из рисунка видно, что ЕC₂D равносторонний, откуда С₂E=C₂D=ED=l₂. Составив теперь пропорцию, найдем, что

, V_E = V_D = 1,5 м/c. (5)

Определяем _DE. Так как МЦС стержня 2 известен (точка С₂) и , то

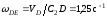. (6)

5. Определяем .

(7)

и . (8)

. (9)

т.к. ω₄ – величина постоянная

Изображаем на чертеже в точке B векторы: (вдоль ВА от В к А)

и (в любую сторону перпендикулярно ВА); численно . Найдя ₃ с помощью построенного МЦС C₃ стержня 3, получим

и .

Спроектируем обе части равенства (7) на направление ВА (ось х), перпендикулярное неизвестному вектору . Тогда получим

. (10)

6. Определяем _BA. Чтобы найти _BA, сначала определим . Для этого обе части равенства (7) спроектируем на направление, перпендикулярное АВ (ось у). Тогда получим

. (11)

Подставив в равенство (11) числовые значения всех величин, найдем, что . Знак указывает, что направление противоположно направлению, показанному на рисунке.

Из равенства получим .

Ответ: V_А =3 м/c; V_E =1,5 м/c; _DE =1,25 c^-1; ; _BA =17,1c^-2.