5.3. Решение задачи с помощью Microsoft Excel

Для решения данной задачи заполним лист Excel так, как это показано на рис. 5.2.

Рис. 5.2

Содержимое ячеек таблицы:

Переменные

Ячейка	Содержательный смысл
B3	Количество изделий вида 1 ()
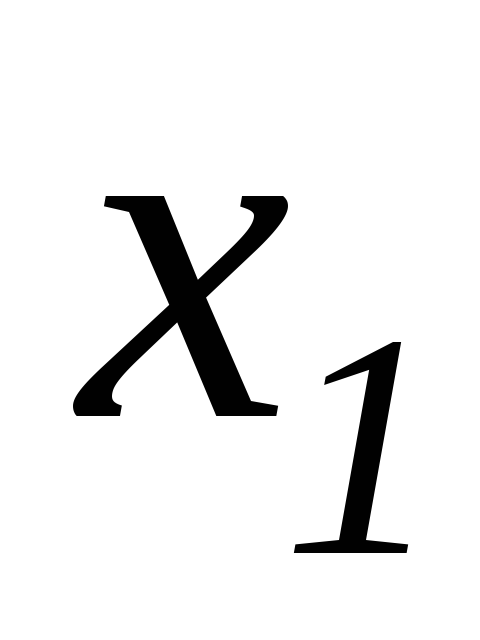B4	Количество изделий вида 2 ()
B5	Количество изделий вида 3 ()

Исходные данные

Ячейка	Содержательный смысл
D3	Прибыль от продажи одного изделия вида 1
D4	Прибыль от продажи одного изделия вида 2
D5	Прибыль от продажи одного изделия вида 3
D13	Предельное время использования операции 1 в течение суток
D14	Предельное время использования операции 2 в течение суток
D15	Предельное время использования операции 3 в течение суток
H3:J5	Длительности операций обработки изделий

Соотношения (формулы)

Ячейка	Содержательный смысл	Формула
D7	Значение целевой функции - величина прибыли за сутки	B3*I11 + B4*I12 + B5*I13 (можно было использовать функцию СУММПРОИЗВ(B3:B5; I11: I13) )
B13	Фактическое время использования опе­рации 1 в течение суток	B$3*H3+B$4*I3+B$5*J3
B14	Фактическое время использования опе­рации 2 в течение суток	B$3*H4+B$4*I4+B$5*J4
B15	Фактическое время использования опе­рации 3 в течение суток	B$3*H5+B$4*I5+B$5*J5

Для того, чтобы выводить в ячейках формулы вместо их значений, необходимо в меню Сервис выбрать команду Параметры, а затем в диалоговом окне Параметры в группе переключателей Параметры окна установить флажок формулы . После этого лист будет иметь вид, показанный на рис. 5.3.

Рис. 5.3

5.4. Нахождение оптимального решения с помощью процедуры поиска решения

1. В меню Сервис выберите команду Поиск решения. Если команда Поиск решения отсутствует в меню Сервис, доустановите соответствующую надстройку (см. пункт 4.3.8).

2. В поле Установить целевую ячейку, введите адрес или имя ячейки, в которой находится формула целевой функции оптимизируемой модели. Можно эту ячейку указать непосредственно на рабочем листе, указав на нее мышью.

3. Чтобы максимизировать значение целевой ячейки путем изменения значений влияющих ячеек, установите переключатель в положение максимальному значению.

Для того чтобы минимизировать значение целевой ячейки путем изменения значений влияющих ячеек, установите переключатель в положение минимальному значению.

Если вы хотите установить значение целевой ячейки равным некоторому числу путем изменения значений влияющих ячеек, установите переключатель в положение значению и введите в соответствующее поле требуемое число.

4. В поле Изменяя ячейки введите имена или адреса изменяемых ячеек, разделяя их знаком точка с запятой или выделите необходимый диапазон ячеек непосредственно на листе.

5. Для автоматического поиска всех ячеек, влияющих на формулу целевой функции модели, нажмите кнопку Предположить.

6. В список Ограничения, введите все ограничения, накладываемые на искомое решение.

7. Нажмите кнопку Выполнить.

А теперь вернемся к нашей задаче определения ассортимента выпуска продукции. На рис. 5.4 представлено диалоговое окно Поиск решения.

Рис. 5.4

Ограничения $B$13 <= $D$13, $B$14 <= $D$14, $B$15 <= $D$15 задают ограничения на время использования операций в течение суток. Ограничения $B$3:$B$5 = ^целое связаны с условиями, по которому количества изделий - суть целые числа.

После нажатия кнопки Параметры в диалоговом окне Параметры поиска решения дополнительно указываются некоторые параметры процесса решения, такие как: максимальное время поиска решения, предельное число итераций, относительная погрешность, допустимое отклонение, линейная ли модель, накладываются ли на переменные условия неотрицательности, показывать ли результаты итераций, метод решения, тип производных, оценка, а также загрузить или сохранить модель (см. рис. 5.5).

Рис. 5.5

После того, как все параметры и ограничения будут установлены, нажатием кнопки Выполнить диалогового окна Поиск решения задача решается.