Теоретические сведения:

Теперь рассмотрим ограничение типа “”. В ЗЛП в канонической форме оно выглядит так:

,

где — избыточная переменная.

Пусть теперь правая часть станет равной :

.

Это уравнение можно переписать в виде:

.

Следовательно, если в оптимальном решении переменная небазисная, то её изменение повлияет на вектор базисных переменных так:

.

С учетом того, что вектор x_B должен быть неотрицательным, получаем необходимость следующего соотношения:

;

.

Таким образом, получили систему из m неравенств:

.

Если , то соответствующее неравенство примет вид: .

Если , то соответствующее неравенство таково: .

Таким образом, допустимый диапазон изменений величины:

.

Если нет ни одного , то , если нет ни одного , то .

В нашей задаче:

Переменная s₄ – небазисная, следовательно, ресурс 4 – дефицитный. Исходное ограничение имеет знак "", тогда допустимый диапазон изменений величины таков (знаменатели дробей взяты из столбца s₄ оптимальной симплекс-таблицы, см. рис. 6.8):

,

Имеем совпадение с результатами Excel (рис. 6.9).

Абсолютный диапазон изменения правой части ограничения:

10 -  b₄  10 + 4, или 7,7(7)  b₄  14.

Проанализируем последствия изменения правой части последнего ограничения модели: 2 x ₁ - x₂ + x₃ = 0 (соотношение объемов выпечки ватрушек, сушек и пирожков).

Ограничения такого рода обычно являются ограничениями на комплектность выпуска продукции. В этом случае правая часть ограничения по сути не может принимать значение, отличное от нуля. Если допустить возможность изменения значения правой части, то при анализе этого ресурса вопрос можно было бы поставить так: на какую величину сумма удвоенного объёма выпечки ватрушек и объёма выпечки пирожков может превышать (или быть меньше) объёма выпечки сушек. В таком контексте ограничение перестаёт быть ограничением-требованием комплектности продукции.

Рис. 6.9.

При нахождении начального допустимого решения, это ограничение содержало искусственную базисную переменную R₃ (эту переменную можно рассматривать как неотрицательную остаточную, поэтому для определения диапазона изменений b₅ используется соотношение (1)).

;

–5  ₅  5;

0 - 5  b₅  0 + 5, или - 5  b₅  5 .

6.6.2. Изменение коэффициентов целевой функции

Существует диапазон изменения коэффициентов целевой функции как базисных, так и небазисных переменных, в которых полученное решение остается оптимальным. Изменение коэффициента базисной переменной в пределах этого диапазона приводит к изменению значения целевой функции, так как , а одна из компонент вектора изменяется. Изменение коэффициента небазисной переменной не меняет значение задачи.

6.6.2.1. Небазисные переменные Теоретические сведения

Изменение коэффициента целевой функции небазисной переменной влияет на относительную оценку только этой переменной.

Пусть новое значение коэффициента целевой функции равно . Отно­сительная оценка небазисной переменной вычисляется по формуле :

,

С учетом изменения коэффициента целевой функции “новое” значение относительной оценки переменной таково:

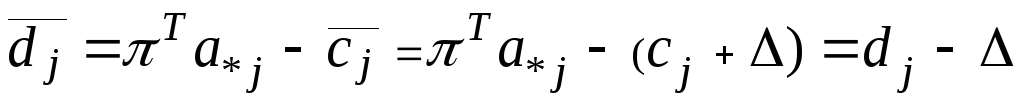
Итак, для небазисной переменной диапазон устойчивости, в котором c_j может изменяться, задается выражением

c_j + ,

где -     , а - относительная оценка переменной x_j, отвечающая оптимальному решению.

В нашей задаче, как видно из оптимальной симплекс-таблицы (рис. 6.10), переменная x₄ является небазисной, значит для неё - < ₄ < 16, что совпадает с результатами Excel (соответствующий фрагмент Отчета по устойчивости приведен на рис. 6.11). Тогда, с учетом начальных значений, диапазон изменения коэффициента целевой функции при данной переменной : - < c₄ < 2+16 или - < c₄ < 18.

Б.п.	x1	x2	x3	x4	s1	s2	s3	s4	R1	R2	R3	Реш.
z (max)	0	0	0	16	17/4	0	0	13/4				265
x1	1	0	0	0	1/4	0	0	5/4	0	-5/4	1	5
s2	0	0	0	0	-1/2	1	0	5/2	0	-5/2	0	20
x2	0	1	0	1	1/4	0	0	1/4	0	-1/4	0	15
s3	0	0	0	-1	5/4	0	1	13/4	-1	-13/4	2	30
x3	0	0	1	1	-1/4	0	0	-9/4	0	9/4	-1	5

Рис. 6.10.

Рис. 6.11