
- •3. Аналитическая геометрия в пространстве
- •3.1. Плоскость в пространстве
- •3.2. Уравнение прямой в пространстве
- •2.3. Проекция вектора на заданную ось. Координаты вектора в декартовой системе координат
- •2.4. Скалярное произведение двух векторов
- •2.5. Векторное и смешанное произведения векторов
- •2.2. Векторы. Линейные операции над векторами
- •1.3. Умножение матриц
- •1.4. Обратная матрица
- •1.5. Ранг матрицы. Элементарные преобразования матриц
- •1.7. Системы линейных алгебраических уравнений
- •1.8. Метод Гаусса решения систем линейных уравнений (метод последовательного исключения неизвестных)
- •1.9. Метод Крамера решения системы n линейных уравнений с n неизвестными
1.10. Решение
систем уравнений матричным методом
Рассмотрим
систему n
уравнений с n
неизвестными (2). Система (2)
эквивалентна матричному уравнению
Если
Решение
системы
2. векторная
алгебра
2.1. Координаты
точки пространства
в
прямоугольной декартовой системе
координат
Если
задана прямоугольная система координат,
то точка пространства М
задается тремя координатами: абсциссой
–
x,
ординатой –
y
и аппликатой
z.
Таким образом, точка, заданная тремя
координатами, обозначается
Пусть
заданы точки
Если
точка С
делит отрезок АВ
так, что
Координаты
середины отрезка АВ
Величина,
для задания которой необходимо указать
ее численное значение и направление,
называется векторной или вектором.
Векторы
изображаются направленными отрезками
и обозначаются
Численное
значение векторной величины называется
длиной или модулем вектора и обозначается
Если
Два
вектора называются коллинеарными,
если они параллельны одной прямой
(обозначение
Три
вектора называются компланарными, если
они параллельны одной плоскости.
Два
вектора равны, т.е.
Из
определения равенства векторов следует,
что параллельное перемещение не меняет
вектора. Этим свойством можно
воспользоваться, чтобы привести векторы
к общему началу.
Сложение
векторов. Сумму
нескольких векторов можно найти по
правилу многоугольника: чтобы
найти вектор – сумму заданных
векторов-слагаемых, нужно последовательно
совместить начало следующего
вектора-слагаемого с концом предыдущего,
тогда вектор, начало которого совпадает
с началом первого вектора, а конец – с
концом последнего, называется суммой
заданных векторов.
Умножение
вектора на скаляр. Пусть
Свойства
умножения вектора на скаляр:
1)
Критерий
коллинеарности двух векторов:
Если
задан ненулевой вектор
Векторы
Любые
два неколлинеарных вектора на плоскости
линейно независимы, т.е. если
Любые
три некомпланарных вектора
Три
некомпланарных вектора
![]() ,
где
,
где
 ,
,
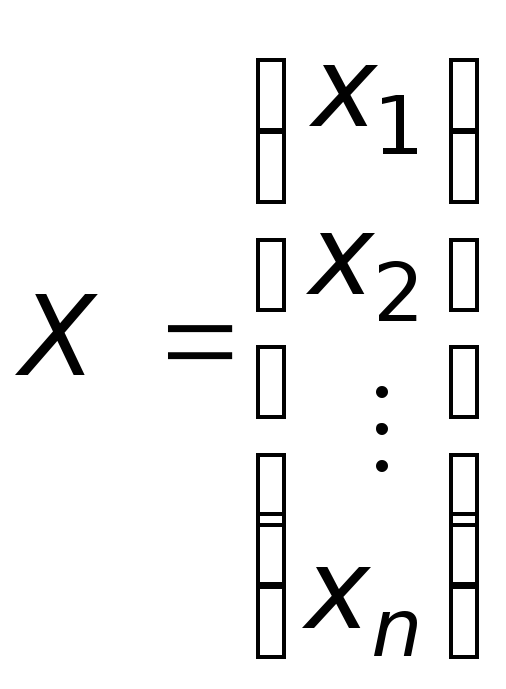 ,
,
 .
.![]() то система (2) имеет единственное решение
(теорема Крамера) и для матрицы А
существует обратная матрица. Тогда
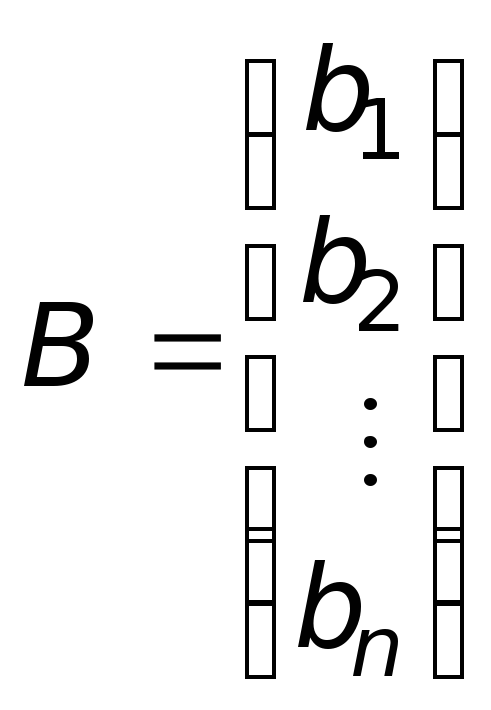
то система (2) имеет единственное решение
(теорема Крамера) и для матрицы А
существует обратная матрица. Тогда
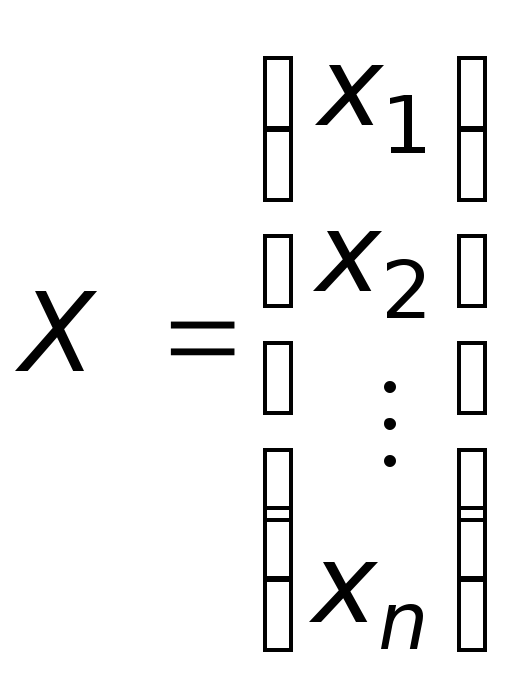
![]()
![]()
![]()
![]()
![]() .
.
 .
.![]() .
.![]() и
и
![]() .
Тогда расстояние
.
Тогда расстояние
![]() .
(3)
.
(3)![]() ,
то
,
то![]() (4)
(4)![]()
2.2. Векторы. Линейные операции над векторами
![]() или
или
![]() ,
где точки
,
где точки
![]() и
и
![]() –
начало и конец вектора.
–
начало и конец вектора.![]() или
или
![]() .
.![]() ,
то
,
то
![]() – нулевой вектор; направление нулевого
вектора произвольно.
– нулевой вектор; направление нулевого
вектора произвольно.![]() ).
).![]() ,
если выполнены три условия:
,
если выполнены три условия: ![]() =
=![]() ;
;
![]() ;
;
![]() и
и
![]() одинаково направлены.
одинаково направлены.![]() – вектор,
– скаляр, тогда
– вектор,
– скаляр, тогда
![]() – вектор, обладающий следующими
свойствами: а)
– вектор, обладающий следующими
свойствами: а) ![]() ;
б)
;
б) ![]() ;
в)
;
в) ![]() сонаправлен
вектору
сонаправлен
вектору
![]() ,
если
,
если
![]() ,
и направлен противоположно, если
,
и направлен противоположно, если
![]() .
.![]()
![]() ;
2)
;
2) ![]() ;
3)
;
3) ![]() ;
4) если
;
4) если
![]() ,
то либо
,
то либо
![]() ,
либо
,
либо
![]() .
.![]() ,
если
,
если
![]() .
.![]() ,
то единичный вектор того же направления
,
то единичный вектор того же направления
![]() называется ортом вектора
называется ортом вектора
![]() .
.![]() называются линейно независимыми, если
равенство
называются линейно независимыми, если
равенство
![]() выполняется только при условии, что
выполняется только при условии, что
![]() при всех
при всех
![]() .
.![]() и
и
![]() не коллинеарны, то из
не коллинеарны, то из
![]() и наоборот; два неколлинеарных вектора
на плоскости образуют базис, и всякий
третий вектор этой плоскости можно
представить в виде
и наоборот; два неколлинеарных вектора
на плоскости образуют базис, и всякий
третий вектор этой плоскости можно
представить в виде
![]() ,
разложив его по базису (
,
разложив его по базису (![]() ,
,
![]() ).
Числа
и
в этом случае называются координатами
вектора
).
Числа
и
в этом случае называются координатами
вектора
![]() в базисе (
в базисе (![]() ,
,
![]() ).
Разложение вектора
).
Разложение вектора
![]() по базису (
по базису (![]() ,
,
![]() )
единственно, т.е. координаты
и
можно найти единственным образом.
)
единственно, т.е. координаты
и
можно найти единственным образом.![]() ,
,
![]() ,
,
![]() в пространстве линейно независимы и
образуют
базис
трехмерного пространства; всякий
четвертый вектор
в пространстве линейно независимы и
образуют
базис
трехмерного пространства; всякий
четвертый вектор
![]() этого пространства можно единственным
образом
разложить по базису (
этого пространства можно единственным
образом
разложить по базису (![]() ,
,
![]() ,
,
![]() ),
т.е. представить в виде
),
т.е. представить в виде
![]() ,
где ,
,
– координаты вектора
,
где ,
,
– координаты вектора
![]() в базисе (
в базисе (![]() ,
,
![]() ,
,
![]() ).
).![]() ,
,
![]() ,
,
![]() образуют правую тройку векторов, если
из конца вектора
образуют правую тройку векторов, если
из конца вектора
![]() кратчайший поворот от
кратчайший поворот от
![]() к
к
![]() виден в положительном (против часовой
стрелки) направлении.
виден в положительном (против часовой
стрелки) направлении.
