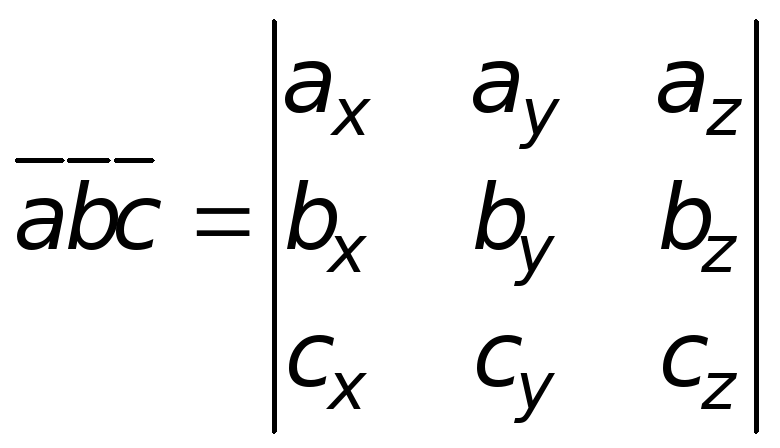- •3. Аналитическая геометрия в пространстве
- •3.1. Плоскость в пространстве
- •3.2. Уравнение прямой в пространстве
- •2.3. Проекция вектора на заданную ось. Координаты вектора в декартовой системе координат
- •2.4. Скалярное произведение двух векторов
- •2.5. Векторное и смешанное произведения векторов
- •2.2. Векторы. Линейные операции над векторами
- •1.3. Умножение матриц
- •1.4. Обратная матрица
- •1.5. Ранг матрицы. Элементарные преобразования матриц
- •1.7. Системы линейных алгебраических уравнений
- •1.8. Метод Гаусса решения систем линейных уравнений (метод последовательного исключения неизвестных)
- •1.9. Метод Крамера решения системы n линейных уравнений с n неизвестными
Проекцией
точки А
на заданную ось называется точка –
основание перпендикуляра, опущенного
из точки А
на ось.
Проекцией
вектора
где
Векторы
Правая
тройка взаимно ортогональных ортов
Координатами
вектора в декартовом базисе являются
проекции этого вектора на оси координат.
Разложение вектора
Пусть
Косинусы
углов, которые вектор
Пусть
Скалярным
произведением векторов
Свойства
скалярного произведения: 1)
Согласно
определению скалярного произведения
и его свойствам
где
Условие
ортогональности векторов имеет вид
Если
Если
Для
базисных векторов
Векторным
произведением вектора
Свойства
векторного произведения:
1)
2)
3)
4)
5) если
Условие
коллинеарности векторов
Смешанным
произведением трех векторов
Свойства
смешанного произведения:
1)
2)
Условие
компланарности векторов:
Объем
параллелепипеда, построенного на
векторах
Объем
пирамиды, образованной векторами,
Если
2.3. Проекция вектора на заданную ось. Координаты вектора в декартовой системе координат
![]() на ось
на ось
![]() называется величина отрезка
называется величина отрезка
![]() ,
заключенного между проекциями начала
и конца вектора
,
заключенного между проекциями начала
и конца вектора
![]() .
Обозначим
.
Обозначим
![]() проекцию вектора
проекцию вектора
![]() на ось
на ось
![]() ;
;
![]() –
проекцию вектора
–
проекцию вектора
![]() на направление
на направление
![]() .
Очевидно, что
.
Очевидно, что
![]() ,
если угол между
,
если угол между
![]() и
и
![]() острый, и
острый, и
![]()
![]() ,
если угол между векторами
,
если угол между векторами
![]() и
и
![]() – тупой (рис.8). Проекцию можно вычислить
по формуле
– тупой (рис.8). Проекцию можно вычислить
по формуле![]() ,
,![]() – угол наклона вектора
– угол наклона вектора
![]() к оси
к оси
![]() .
.![]() и
и
![]() называются ортогональными
(
называются ортогональными
(![]() ),
если параллельны двум взаимно
перпендикулярным прямым.
),
если параллельны двум взаимно
перпендикулярным прямым.![]() образует декартов базис
образует декартов базис
![]() .
.![]() в декартовой системе координат
обозначается
в декартовой системе координат
обозначается
![]()
![]() .
.![]() ,
,
![]() .
Тогда
.
Тогда
![]() ;
;
![]() ;
;![]() .
.![]() образует с осями координат, называются
направляющими косинусами вектора
образует с осями координат, называются
направляющими косинусами вектора
![]() :
:![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.![]() и
и
![]() – точки пространства, тогда
– точки пространства, тогда![]() .
.
2.4. Скалярное произведение двух векторов
![]() и
и
![]() называется скаляр (число)
называется скаляр (число)
![]() .
.![]() ;
2)
;
2) ![]() ;
3)
;
3) ![]() -
скаляр,
-
скаляр,
![]()
![]() .
.![]() ;
;
![]() ;
;
![]() ,
(8)
,
(8)![]() – скалярный квадрат вектора
– скалярный квадрат вектора
![]() .
.![]() .
.
![]()
![]() то
то![]() .
.![]() .
(9)
.
(9)![]() справедливы равенства
справедливы равенства![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.2.5. Векторное и смешанное произведения векторов
![]() на вектор
на вектор
![]() называется вектор
называется вектор
![]() ,
который определяется следующим образом:
а)
,
который определяется следующим образом:
а)
![]() ,
т.е.
,
т.е.
![]() численно равен площади параллелограмма,
построенного на векторах-сомножителях
как на сторонах; б)
численно равен площади параллелограмма,
построенного на векторах-сомножителях
как на сторонах; б) ![]() и
и
![]() ;
в)
;
в) ![]() ,
,
![]() ,
,
![]() образуют правую тройку векторов.
образуют правую тройку векторов.![]() ;
;![]() ,
где
- скаляр;
,
где
- скаляр;![]() ;
;![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
где
,
где
![]() – координатные орты;
– координатные орты;
![]() и
и
![]() ,
то
,
то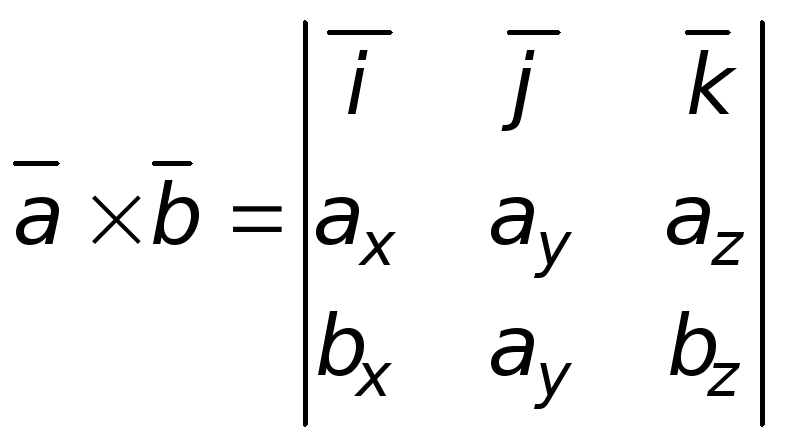 .
(10)
.
(10)![]() .
.![]() ,
,
![]() и
и
![]() называется скалярное произведение
вектора
называется скалярное произведение
вектора
![]() на вектор
на вектор
![]() .
Смешанное произведение векторов
обозначается
.
Смешанное произведение векторов
обозначается
![]() .
.![]() ;
(11)
;
(11)![]() ,
но
,
но
![]() .
.![]() тогда и только тогда, когда
тогда и только тогда, когда
![]() ,
,
![]() ,
,
![]() компланарны и не равны нулю.
компланарны и не равны нулю.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.
![]() ,
,
![]() и
и
![]() ,
то
,
то