
- •3. Аналитическая геометрия в пространстве
- •3.1. Плоскость в пространстве
- •3.2. Уравнение прямой в пространстве
- •2.3. Проекция вектора на заданную ось. Координаты вектора в декартовой системе координат
- •2.4. Скалярное произведение двух векторов
- •2.5. Векторное и смешанное произведения векторов
- •2.2. Векторы. Линейные операции над векторами
- •1.3. Умножение матриц
- •1.4. Обратная матрица
- •1.5. Ранг матрицы. Элементарные преобразования матриц
- •1.7. Системы линейных алгебраических уравнений
- •1.8. Метод Гаусса решения систем линейных уравнений (метод последовательного исключения неизвестных)
- •1.9. Метод Крамера решения системы n линейных уравнений с n неизвестными
Каждая
плоскость определяется уравнением
первой степени в декартовых координатах,
и всякое уравнение первой степени
задает плоскость.
Общее
уравнение плоскости
при
Всякий
(отличный от нуля) вектор
Уравнение
плоскости, проходящей через точку
Уравнение
плоскости, проходящей через три заданные
точки
Уравнение
плоскости в отрезках
где
a, b, c
– отрезки, отсекаемые плоскостью на
осях Ox, Oy, Oz
соответственно (плоскость проходит
через точки
Нормальное
уравнение плоскости
где
Общее
уравнение плоскости (12) приводится к
нормальному виду (16) умножением (12) на
нормирующий множитель
Расстояние
от точки
Пусть
заданы две плоскости:
где
Условия параллельности
и перпендикулярности заданных плоскостей
имеют вид соответственно
Если
заданные плоскости не параллельны, то
множество плоскостей, проходящих через
прямую их пересечения, называется
пучком плоскостей. Уравнение любой
(кроме второй из заданных) плоскостей
можно выделить из уравнения пучка
плоскостей подбором параметра
Прямую
можно задать как линию пересечения
двух плоскостей системой уравнений
Канонические
уравнения прямой, параллельной вектору
Вектор
Параметрические
уравнения прямой
При
параметре t,
меняющемся от
Уравнения
прямой, проходящей через две заданные
точки
Пусть
заданы две прямые
Углом
между двумя прямыми называется угол
между векторами
Условие
параллельности и перпендикулярности
двух прямых соответственно
Направляющими
косинусами прямой называются направляющие
косинусы вектора
3. Аналитическая геометрия в пространстве
3.1. Плоскость в пространстве
![]() (12)
(12)![]() .
.![]() ,
перпендикулярный к данной плоскости,
называется
нормальным вектором плоскости или
нормалью.
В уравнении (12) коэффициенты А,
В, С
– координаты вектора нормали плоскости.
,
перпендикулярный к данной плоскости,
называется
нормальным вектором плоскости или
нормалью.
В уравнении (12) коэффициенты А,
В, С
– координаты вектора нормали плоскости.![]() перпендикулярно вектору
перпендикулярно вектору
![]() ,
имеет вид
,
имеет вид![]() .
(13)
.
(13)![]() ,
,
![]() и
и
![]() ,
записывают в виде
,
записывают в виде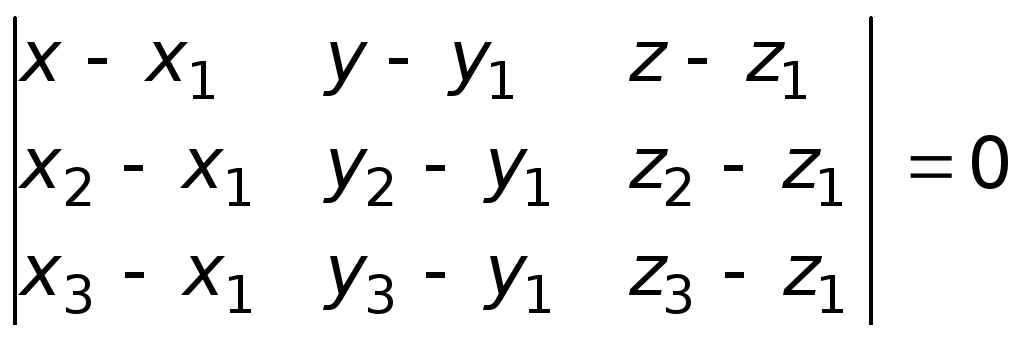 .
(14)
.
(14)![]() ,
(15)
,
(15)![]() ,
,
![]() ,
,
![]() ).
Заметим, что если плоскость проходит
через начало координат, то ее
невозможно задать уравнением в
отрезках.
).
Заметим, что если плоскость проходит
через начало координат, то ее
невозможно задать уравнением в
отрезках.![]() ,
(16)
,
(16)![]() ,
,
![]() ,
,
![]() – направляющие косинусы вектора
нормали; р –
расстояние от начала координат до
плоскости.
– направляющие косинусы вектора
нормали; р –
расстояние от начала координат до
плоскости.
![]() (знак
(знак
![]() выбирается так, чтобы
выбирается так, чтобы
![]() ).
).![]() до плоскости
до плоскости
![]()
![]() .
(17)
.
(17)![]() и
и
![]() .
Двугранный угол
.
Двугранный угол
![]() ,
образованный двумя заданными плоскостями,
называется углом между этими плоскостями:
,
образованный двумя заданными плоскостями,
называется углом между этими плоскостями:![]() ,
,![]() и
и
![]() – векторы-нормали к заданным плоскостям.
– векторы-нормали к заданным плоскостям.![]() ;
;
![]() .
.![]() :
:![]() .
(18)
.
(18)3.2. Уравнение прямой в пространстве
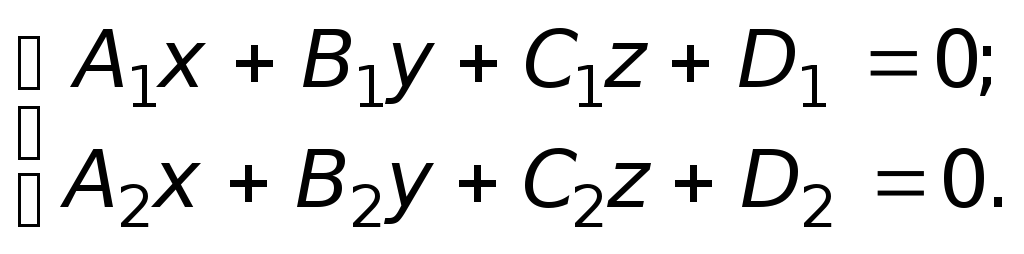
![]() и проходящей через точку
и проходящей через точку
![]() ,
имеют вид
,
имеют вид![]() .
(19)
.
(19)![]() ,
параллельный прямой, называется
направляющим вектором прямой.
,
параллельный прямой, называется
направляющим вектором прямой.
![]() до
до
![]() ,
текущая точка
,
текущая точка
![]() пробегает всю прямую.
пробегает всю прямую.![]() и
и
![]() ,
,![]() .
(20)
.
(20)![]() и
и
![]() .
.![]() и
и
![]() ;
;![]() .
(21)
.
(21)![]() ;
;![]() .
.![]() .
.
